ТЕХНОЛОГИЧЕСКИЕ ПРОЦЕССЫ МАШИНОСТРОИТЕЛЬНОГО ПРОИЗВОДСТВА

Понятие о размерной цепи

При конструировании механизмов, машин, приборов и других изделий, проек­тировании технологических процессов, выборе средств и методов измерений воз­никает необходимость в проведении размерного анализа, с помощью которого достигается рациональная простановка размеров, нормирование их точности. Под размером в данном случае понимают любые размерные связи между геометриче­скими элементами изделия, то есть линейные и угловые размеры, отклонения формы и расположения поверхностей, параметры шероховатости и волнистости поверхностей, параметры, характеризующие глубину слоев покрытия, насыще­ния, изменение состояния материала и т. п.

Размерный анализ проводят с использованием различных методик расчета размерных цепей. Одним из нормативных документов, регламентирующих основ­ные понятия и определения, используемые при расчете размерных цепей, являют­ся методические указания [4]. В соответствии с этими указаниями, размерной це­пью называют совокупность размеров, непосредственно участвующих в решении поставленной задачи и образующих замкнутый контур. Однако при конструиро­вании изделий и при проектировании технологических процессов изготовления деталей можно применять расширенное толкование понятия размерной цепи.

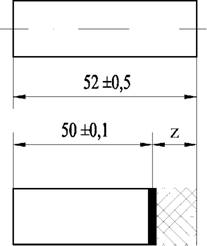
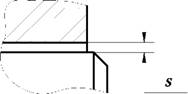
Размерной цепью можно назвать совокупность последовательно связанных размеров. Размерные цепи отражают размерные связи между геометрическими элементами деталей, сборочных единиц, изделий в сфере конструирования и экс­плуатации, между элементами заготовок на разных стадиях технологических про­цессов в сфере технологического проектирования и изготовления и т. п. При таком подходе размерные цепи могут быть разомкнутыми и замкнутыми. Например, на чертежах деталей обычно указывают только те размеры, которые необходимы для изготовления. В этом случае связь между геометрическими элементами отражает­ся в виде разомкнутой размерной цепи (рис. 6.1, а). Иногда на чертеже указывают дополнительные размеры, отмечаемые знаком *. В этом случае в технических требованиях записывают: «* Размеры для справок». При наличии таких размеров возникают замкнутые размерные цепи (рис. 6.1, б). При проектировании техноло­гических процессов указывают размеры на разных стадиях обработки. Размеры до и после механической обработки образуют разомкнутые цепи. Если же указать между этими размерами снимаемый припуск z (рис. 6.1, в), то цепь становится замкнутой.

Размеры, входящие в размерную цепь, называют звеньями. Звенья разомкну­той размерной цепи, которые предписаны к изготовлению и контролю, называют составляющими. Звено, введение которого в разомкнутую размерную цепь пре­вращает ее в замкнутую, называют замыкающим. В замкнутой размерной цепи может быть только одно замыкающее звено, а остальные звенья цепи являются составляющими. Расчет размерных цепей возможен только для замкнутых цепей

До обработки

40 ±0,2

90-0,7

После обработки

50

90-0,7

* Размеры для справок Рис. 6.1. Примеры размерных цепей: а) разомкнутых; б), в) замкнутых

И связан с определением числовых характеристик одних звеньев цепи по извест­ным характеристикам других.

В зависимости от расположения звеньев в пространстве размерные цепи под­разделяют на линейные, плоские и пространственные. К линейным относят цепи, звенья которых определяют размерные связи между геометрическими элементами в одном координатном направлении.

Рассмотрим вначале теоретические и методические положения, связанные с расчетом простых линейных цепей.

Простой линейной цепью будем называть цепь, удовлетворяющую следую­щим требованиям:

1) звенья цепи - линейные размеры, лежащие на одной прямой или на парал­лельных прямых линиях;

2) количество составляющих звеньев цепи - не менее двух;

3) составляющие звенья цепи независимы между собой;

4) величина каждого составляющего звена может принимать только положи­тельные значения, включая 0.

В простой линейной размерной цепи числовые характеристики замыкающего звена связаны с характеристиками составляющих звеньев наиболее простыми за­висимостями.

Для расчета каждую размерную цепь удобно представить в виде схемы. На схеме простой линейной цепи звенья изображают отрезками прямых параллель­
ных линий с двухсторонними стрелками. Составляющие звенья на схеме цепи изображают одинарной линией, а замыкающее звено - двойной. При выполнении схемы важно отразить характер связи между геометрическими элементами и не­обязательно соблюдение масштаба. Каждую размерную цепь обозначают пропис­ными буквами русского алфавита А, Б, В и т. д. Звенья цепи обозначают той же буквой с индексами: 0 - для замыкающего звена, 1, 2, 3 и т. д. - для составляющих звеньев. Нумерация составляющих звеньев может быть произвольной, например, по порядку следования звеньев, начиная от замыкающего звена в принятом направлении обхода (рис. 6.2).

А і =90 - о,7

Л 2 =40 ±0,2

А з =30 - од

А

Рис. 6.2. Схема размерной цепи А: А1 - увеличивающее звено; А2, A3 - умень­шающие звенья; А0 - замыкающее звено

Составляющие звенья простой линейной размерной цепи по характеру влия­ния на величину замыкающего звена можно разделить на увеличивающие и уменьшающие. Увеличивающими называют составляющие звенья, при увеличе­нии которых замыкающее звено увеличивается. Уменьшающими называют со­ставляющие звенья, при увеличении которых замыкающее звено уменьшается.

Для разделения составляющих звеньев на увеличивающие и уменьшающие используют правило обхода, согласно которому при движении по звеньям замк­нутой размерной цепи сопоставляют направления движения по составляющим звеньям с направлением движения по замыкающему звену. Составляющее звено, направление движения по которому совпадает с направлением движения по за­мыкающему, является уменьшающим. Если движение по составляющему звену происходит в противоположном направлении по отношении к замыкающему зве­ну, то это означает, что данное составляющее звено является увеличивающим. Движение обычно начинают с замыкающего звена. Направление движения по за­мыкающему звену может быть любым.

Для определенности выберем направление слева направо (см. рис. 6.2). Тогда:

1) составляющее звено, движение по которому выполняется слева направо, от­носят к уменьшающим;

2) составляющее звено, движение по которому выполняется справа налево, от­носят к увеличивающим.

2?2=50d8(;°'°89)

B0=z

=>

Рис. 6.3. Примеры простых размерных цепей:

А) эскиз сопряжения вала со втулкой; в) схема обработки при фрезеровании;

Б) схема размерной цепи сопряжения; г) схема размерной цепи припуска

Согласно данному правилу в размерной цепи, показанной на рис. 6.2, звено А1 является увеличивающим, а звенья А2 и А3 - уменьшающими.

Примерами простых размерных цепей являются: цепь зазора s в сопряжении вала с втулкой и цепь припуска z, снимаемого при фрезеровании плоскости (рис. 6.3).

При расчетах размерных цепей используют символическую запись цепи в виде уравнения. Обычно в левой части уравнения располагают символ замыкающего звена, то есть А, Б0, В0 и т. д. В правой части уравнения записывают алгебраи­ческую сумму символов составляющих звеньев, причем символы увеличивающих звеньев записывают со знаком «+», а символы уменьшающих звеньев - со знаком «-». В соответствии с этим уравнение рассмотренной цепи А будет иметь вид А = А1 - А2 - А3. Это уравнение называют основным уравнением цепи, так как оно отражает связь основных характеристик звеньев: номинальных размеров, средних размеров и математических ожиданий размеров. Основные уравнения цепей, схемы которых изображены на рис. 6.3, имеют вид: Б0 = Б1 - Б2; В0 = В1 - В2. Для схемы, изображенной на рис. 6.4, уравнение цепи будет

Гп

АП = 2 Аув - 2 Аум ; АП = £1А1 + £2 А2 + + Јn Ап ;

А) = 22 £ 4,

I=1

Где 2 Аув и 2 Аум - сумма характеристик увеличивающих и уменьшающих звеньев; £ - коэффициент передачи (передаточное отношение), отражающий влияние составляющего звена на замыкающее и в простой линейной цепи равный «+1» - для увеличивающих звеньев, «-1» - для уменьшающих; i - порядковый номер звена в цепи; n - количество составляющих звеньев цепи.

Для уточнения характеристики размера символы записывают с индексом. На­пример, уравнения номиналов, средних размеров и математических ожиданий за­писывают так:

Ан°м = 2£. аном ■ i=1

Ар = 2 £ аср ; i=1

А)0=2 £ амо. i=1