ТЕХНОЛОГИЧЕСКИЕ ПРОЦЕССЫ МАШИНОСТРОИТЕЛЬНОГО ПРОИЗВОДСТВА

Числовые характеристики точности действительных размеров

Действительными называют размеры деталей, установленные в результате из­мерений с допустимой погрешностью. Обычно допустимую погрешность прини­мают по ГОСТ 8051-81. Для количественной оценки точности размеров исполь­зуют различные числовые характеристики. Так о точности размера у отдельно взятой детали судят по величине отклонения ДА действительного размера Ад от

Заданного Аз:

ДА = Ад - Аз.

В качестве заданного принимают средний размер, один из предельных разме­ров или номинальный размер.

Для оценки точности размеров в партии деталей, обработанных в течение не­которого времени на станке, принимают: математическое ожидание Ам0, среднее квадратическое отклонение с, величину поля рассеяния с и др.

Математическое ожидание Ам0 характеризует положение центра рассеяния размеров. Так как при измерении производят округление получаемых размеров с учетом цены деления используемых средств измерения, то получаемые действи­тельные размеры можно считать дискретными случайными величинами. Оценку математического ожидания в этом случае можно определить как среднюю ариф­метическую величину Аса размеров в партии из n деталей

Дса = дмо = i=1

N

Среднее квадратическое отклонение с определяют по имеющимся результа­там измерения размеров в партии деталей. Если число размеров в партии деталей более 50, то для определения с используют формулу

Са 2

I (4 - Аса) i=1

С =

N

Где Аса - средний арифметический размер в партии деталей; Ai - текущий размер каждой детали; n - количество деталей в партии.

Если число размеров в партии деталей менее 50, то рекомендуется формула

Са 2

I (Ai - Аса)

I = 1

С =

N -1

В теории вероятностей и математической статистике доказано, что оценка, по­лученная по этой формуле, дает возможность получить несмещенную оценку

Дисперсии, определяемой как D = с2.

Математическое ожидание и среднее квадратическое отклонение при заданном симметричном законе распределения размеров полностью характеризуют дейст­вительный размер как случайную величину. Наиболее распространенными зако­нами распределения размеров являются нормальный закон, закон равнобедренно­го треугольника и закон прямоугольника.

Для расчета размерных цепей в качестве числовой характеристики размера ис­пользуют поле рассеяния с. Под величиной поля рассеяния понимают такой ин­тервал изменения размеров в партии деталей, за пределами которого оказывается пренебрежимо малая часть деталей. При нормальном законе распределения вели­чину поля рассеяния принимают равной 6с, что соответствует вероятности вы­хода размеров деталей за границы поля рассеяния, равной 0,27%. Для закона рав­нобедренного треугольника и прямоугольника поле рассеяния составляет соот­ветственно 4,9с и 3,46с при вероятности выхода размеров за границы поля рас­сеяния, равной 0%.

Для оценки характера рассеяния размеров используют коэффициент рассея­ния, который определяют по формуле Л = ^^. При расчете размерных цепей ве­с

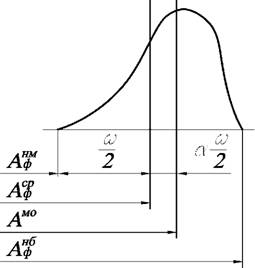
Роятностным методом используют значения коэффициента Л. Для указанных выше законов значения этих коэффициентов принимают по табл. 6.1. При асим­метричных законах распределения (рис. 6.7) для характеристики используют ко­эффициент асимметрии а, определяемый по формуле

А =

С

Где Аср - средний размер между двумя фактическими предельными А равный

А + А

При асимметричном законе распределения математическое ожидание опреде­ляют по формуле

Амо = Аср +аС. (6.4)

Таким образом, при расчете размерных цепей в качестве важнейших числовых

Характеристик должны быть использованы математическое ожидание Амо, поле рассеяния с, коэффициент рассеяния Л и коэффициент асимметрии а. Для сим­метричных законов распределе­ния коэффициент равен нулю, а математическое ожидание равно

Среднему размеру Аср. В этом случае действительный размер можно представить в форме среднего размера с симметрич­ными отклонениями, равными половине поля рассеяния. Эта форма представления размера совпадает с формой среднего размера с симметричными пре­дельными отклонениями, если поле допуска совпадает с полем рассеяния, а закон распределе­ния симметричный.