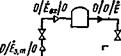Тепловое аккумулиров ание энергии
Эффективность аккумулирования
Как отмечалось в разд. 1.3, важное значение имеет КПД системы аккумулирования (полная эффективность). Высокому КПД системы соответствуют повышенная пиковая мощность, лучшее использование и более низкие затраты топлива. В последующем КПД системы будет определяться на основе учета индивидуальных потерь и эффективности соответствующих типов установок аккумулирования энергии.
3.2.1. Определения
Полный КПД т)ак насосной системы аккумулирования энергии определяется отношением электрической (пиковой) мощности, развиваемой во время разрядки, к электрической мощности, затрачиваемой во время зарядки за цикл (т. е. принимается, что в аккумуляторе условия в начале и в конце цикла одинаковы). В особых случаях, где непосредственно используется механическая энергия, тіак определяется как отношение механических энергий. В общем случае полный КПД г)ак есть отношение эксергий
•Пак = £раз/£з. (3.1)
где Ераз — эксергия разрядки, £3 — эксергия зарядки.
Если за Е3 принять уменьшение электрической энергии в основной системе за счет зарядки, то это же определение может быть применено к безнасосным системам аккумулирования.
Полный КПД Г)ак определяют три величины: £з, с — эксергетический КПД системы зарядки; £ак — эксергетический КПД аккумулирования в соответствии с уравнением (2.99); £раз, с— эксергетический КПД системы разрядки:
TOC o "1-5" h z Лак == £з, с ' ?раз, с * Сак - (3.2)
КПД систем зарядки и разрядки могут быть объединены: Ес = Ь. с’Ераэ. с (3.3)
так что TW = Utc. (3.4)
3.2.2. Насосные системы аккумулирования
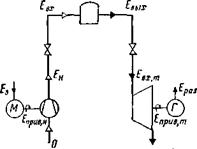
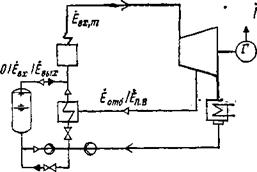
На рис. 3.9 показана простая насосная система. Во время зарядки компрессор (насос) увеличивает эксергию рабочего тела от равновесной с окружающей средой (Е = 0) до Е„. Между выходом из компрессора и входом в аккумулятор будут иметь место потери в трубах (на этом участке может быть также установлен теплообменник, способствующий тепловому аккумулированию). Эти потери уменьшают Е„ до величины Еах. Таким образом, формула для определения КПД системы зарядки приобретает вид
£э. с = EbJE3 = (EJEH)(EJEnmB, „)(£„ рИВ, JE3) = &Ым> (3.5)
где использованы следующие индексы: «вх» — вход в аккумулятор, «з» — зарядка, «прив» — привод насоса или компрессора, «н» — выход насоса или компрессора, С — зона зарядки, Р — зона насоса или компрессора, М — зона двигателя.
Аналогичным образом эффективность разрядки определяется как
Сраз, с == Ер33/Евых == (^раз/^прив, т) (Ецрив, і/Евц, т) {Евх, т/^вых) =
= йоСг£ві (3*6)
Рис. 3.9. Потоки эксергии в насосной аккумулирующей системе.
|
|
где «вых» — выход аккумулятора, «раз» — разрядка, «прив, т» — привод турбины, «вх, т» — вход турбины, D — зона разрядки, Т — зона турбины (или другого расширительного устройства), G — зона генератора.
Поскольку КПД самого аккумулятора определяется отношением
£ак = Евых/Евх, (3.7)
полный КПД г]ак можно записать в виде выражения
Лак — (£с£м£р) Сак (£о£г£о)- (3.8)
Таким образом, полный КПД определяется семью частными показателями эффективности, каждый из которых меньше 1.
3.2.3. Безнасосные системы аккумулирования
На рис. 3.10 показана простая безнасосная система аккумулирования, состоящая из парогенератора, аккумулятора и перегрузочной (пиковой) турбины. В этой системе существуют три потока эксергии Ё:
а) базисная нагрузка
Ёб=Ё**.г‘Ьв, ад
где индексами «б» и TG обозначены базисная нагрузка и турбоагрегат соответственно;
б) зарядка
Ёб - £, = (£„. т - Ё3, т) Єго.(3.10)
в) разрядка через пиковую турбину
(3.11)
где индекс РТ обозначает турбоагрегат пиковой нагрузки.
Так как использование отнесенных ко времени потоков эксергии Ё для определения полной эффективности предпочтительнее, чем эксергий Е (как и в случае рассмотренных
^раз — ^раз. т? РГ>
Зак 414
|
|
|
tut |
і ОІОІЕраз, т
f
^errm * I,, Eify'tJfrEpas
|
4 |
|
-e-<- |
Рис. 3.10. Потоки эксергии в безнасосной аккумулирующей системе.
|
(3.12) |
выше насосных систем аккумулирования), следует использовать интеграл Ё по времени зарядки и разрядки. Если мощность зарядки и разрядки постоянна, то полный КПД безнасосной системы аккумулирования может быть определен формулой
Лак. бн Драз^раз/E3t3,
где /раз — длительность разрядки, t3 — длительность зарядки. Характеристическим параметром безнасосных систем аккумулирования служит относительная мощность зарядки (т. е. отношение мощности зарядки к базисной нагрузке), определяемая как
|
С = £э/£б<1. Используя определения величин КПД £ак == Двьіх^раз/Двх^зі = Драз, т/£вых> £с== Двх/Дз-т |
(3.13)
(3.14)
(3.15)
(3.16)
в уравнениях (3.9) —(3.13), получим полный КПД безнасосной системы в виде
Лак. бн = [?С^1----------------------- ™ */ Г0 У 5гов] £ак [?£> * Х, рЛ - (3.17)
Он определяется тремя частными КПД и, кроме того, содержит отношение КПД турбины пиковой нагрузки и турбины базисной нагрузки во время зарядки £рт/%то з-
Выражение в круглых скобках учитывает изменение КПД турбины в процессе зарядки £гс з (по сравнению с КПД турбины при нормальной работе tro), а также изменение С.
В предельном случае t, Ta = %то з выражение в квадратных скобках становится равным 1; при С да 0 (зарядка происхо-
|
|
|
V ЗО |
|
О O. Z ОА 0,6 0,8 1,0 от нагрузки [1.25]. tpas/h |
|
ЮО |
|
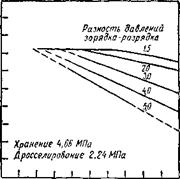
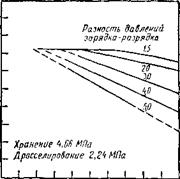
Рис. 3.11. Зависимость полного КПД т),к аккумулирующей установки со скользящим давлением |
|
во |
дит в течение очень длительного времени) в соответствии с правилом Лопиталя имеем
Лак. бн^ "1 ^ Т$'с ГС^)/^Г0з] £ак [£о£рг]- (3,18)
Это уравнение иллюстрирует влияние отклонений КПД турбины в процессе зарядки.
На рис. 3.11 показаны для реального случая [1.25] зависимости полного КПД аккумулятора со скользящим давлением на паросиловой установке от отношения времен разрядки и зарядки. Кривые соответствуют различным значениям разности давлений зарядки и разрядки. Если принять постоянными мощность и длительность разрядки, то отношение времен разрядки и зарядки будет пропорционально относительной мощности зарядки С, определение которой дано выше. С увеличением /Раз//з Пак уменьшается вначале медленно, но затем, со снижением КПД турбины, значительно быстрее. Большой гистерезис давлений зарядки и разрядки приводит к большим потерям на дросселирование во время зарядки и разрядки.
В безнасосных системах аккумулирования, у которых г]ак состоит только из трех частных КПД и двух отношений КПД, возможны высокие значения г|ак. Для системы с постоянными параметрами Е3, т = £раз, т и £с = = 1. Если же КПД тур
боагрегата при частичной и пиковой нагрузках равен КПД турбины на базисной нагрузке, то т]ак стремится к £ак-
3.2.4. Аккумулирование энергии накоплением питательной воды
Аккумулирование посредством питательной воды представляет собой специальный вариант безнасосных систем
|
|
|
tut |
і ОІОІЕраз, т
f
^errm * I,, Eify'tJfrEpas
|
4 |
|
-e-<- |
Рис. 3.10. Потоки эксергии в безнасосной аккумулирующей системе.
|
(3.12) |
выше насосных систем аккумулирования), следует использовать интеграл Ё по времени зарядки и разрядки. Если мощность зарядки и разрядки постоянна, то полный КПД безнасосной системы аккумулирования может быть определен формулой
Лак. бн Драз^раз/E3t3,
где /раз — длительность разрядки, t3 — длительность зарядки. Характеристическим параметром безнасосных систем аккумулирования служит относительная мощность зарядки (т. е. отношение мощности зарядки к базисной нагрузке), определяемая как
|
С = £э/£б<1. Используя определения величин КПД £ак == Двьіх^раз/Двх^зі = Драз, т/£вых> £с== Двх/Дз-т |
(3.13)
(3.14)
(3.15)
(3.16)
в уравнениях (3.9) —(3.13), получим полный КПД безнасосной системы в виде
Лак. бн = [?С^1------------- ™ */ Г0 У 5гов] £ак [?£> * Х, рЛ - (3.17)
Он определяется тремя частными КПД и, кроме того, содержит отношение КПД турбины пиковой нагрузки и турбины базисной нагрузки во время зарядки £рт/%то з-
Выражение в круглых скобках учитывает изменение КПД турбины в процессе зарядки £гс з (по сравнению с КПД турбины при нормальной работе tro), а также изменение С.
В предельном случае t, Ta = %то з выражение в квадратных скобках становится равным 1; при С да 0 (зарядка происхо-
|
|
|
too |
|
V ЗО J? |
|
О O. Z ОА О, В 0,8 1,0 от нагрузки [1.25]. tpas/h |
|
Рис. 3.11. Зависимость полного КПД т),к аккумулирующей установки со скользящим давлением |
|
во |
дит в течение очень длительного времени) в соответствии с правилом Лопиталя имеем
Лак. бн^ "1 ^ Т$'с ГС^)/^Г0з] £ак [£о£рг]- (3,18)
Это уравнение иллюстрирует влияние отклонений КПД турбины в процессе зарядки.
На рис. 3.11 показаны для реального случая [1.25] зависимости полного КПД аккумулятора со скользящим давлением на паросиловой установке от отношения времен разрядки и зарядки. Кривые соответствуют различным значениям разности давлений зарядки и разрядки. Если принять постоянными мощность и длительность разрядки, то отношение времен разрядки и зарядки будет пропорционально относительной мощности зарядки С, определение которой дано выше. С увеличением /Раз//з Пак уменьшается вначале медленно, но затем, со снижением КПД турбины, значительно быстрее. Большой гистерезис давлений зарядки и разрядки приводит к большим потерям на дросселирование во время зарядки и разрядки.
В безнасосных системах аккумулирования, у которых г]ак состоит только из трех частных КПД и двух отношений КПД, возможны высокие значения г|ак. Для системы с постоянными параметрами Е3, т = Драз, т и £с = to = 1. Если же КПД турбоагрегата при частичной и пиковой нагрузках равен КПД турбины на базисной нагрузке, то т]ак стремится к £ак.
3.2.4. Аккумулирование энергии накоплением питательной воды
|
|
|
Рис. 3.12. Потоки эксергии в системе аккумулирования с использованием питательной воды. |
|
igtEg~^3 lEtS*£pia |
Аккумулирование посредством питательной воды представляет собой специальный вариант безнасосных систем
аккумулирования и часто применяется на паросиловых установках с регенеративным подогревом питательной воды. Обычно используются вытеснительные аккумулирующие сосуды, хотя в принципе возможно применение и систем расширительного типа. На рис. 3.12 показана упрощенная схема такой установки. Аккумулирующая система, установленная в параллель с магистралью питательной воды, забирает эту воду во время зарядки и одновременно подает холодную воду в магистраль. Во время разрядки происходит обратный процесс— снижение потока отбора (в предельном случае уменьшение до нуля) и увеличение выдаваемой мощности турбины. На рис. 3.12 показаны потоки эксергии для трех режимов:
а) при базисной нагрузке
|
(3.19) (3.20) (3.21) |
Ёц — £го (Ёвх, т Вотб)
(где индекс «отб» — отбор);
б) при зарядке
Дб — Дэ =® т ~ £отб Двх/Sn. в, з) £гСз>
£п. в ~ Ёя. в/£отб
(где £п. в — эксергетический КПД магистрали питательной воды);
в) при разрядке (с основной турбиной)
(3.22)
|
|
|
(3.23) |
Выполнив арифметические действия, аналогичные указанным в разд. 3.2.3, и введя коэффициент разрядки
D — £раз/£б^ 1>
получим полный КПД:
Ча,.п. в = [Сп. в..(і - Л-уг0)Дгоз]их
X [SrGpas/Sn. B. раз (l Н TOpaJ^TQ _ (3.24)
Это уравнение похоже на уравнение (3.17) для безнасосных систем аккумулирования (разд. 3.2.3), за исключением того, что теперь знаменатель содержит КПД магистрали питательной воды во время разрядки, а следующее за ним выражение в круглых скобках содержит изменение КПД турбоагрегата в процессе разрядки. Отметим, что КПД системы разрядки
Spaa, с == SrG. раз/Sn. B, р. з (l + iZ±^E«£l£) (3.25)
может быть больше 1 (например, если КПД магистрали питательной ВОДЫ £п. В, раз мал). G другой стороны, низкий КПД магистрали питательной воды снижает КПД системы зарядки £з, с, влияя на полный КПД, а также на термический КПД основного процесса.
Только в простых случаях, например рассмотренном выше, полный КПД может быть оценен исходя из частных КПД. Для более сложных систем потребуется расчет с использованием вычислительных программ для термодинамических циклов.
3.2.5. Потери в энергоаккумулирующих установках
В табл. 3.1 дан перечень видов потерь в наиболее важных типах энергоаккумулирующих установок. Установка характеризуется типом аккумулятора, а также типом системы аккумулирования (прямое или косвенное, безнасосное или насосное). Приводятся потери в аккумуляторе и потери в оборудовании зарядки и разрядки. Дается также КПД разрядки, что важно для определения наряду с плотностью запасаемой эксергии (разд. 2.8.2) эксергии разрядки и, следовательно, размеров аккумулятора. Кроме того, приводятся данные по полному КПД всей установки.
Использование при аккумулировании энергии прямого запасания рабочего тела или теплообменной среды — в особенности питательной воды в паровых установках и в первичном цикле солнечных теплоэнергетических установок—приводит к довольно высокому значению т)ак. Высокие значения т]ак (около 0,95) для аккумуляторов со скользящим давлением относятся только к установкам с малым гистерезисом давлений зарядки и разрядки, для которых требуются недорогие сосуды давления.
|
Таблица 3.1. Потери и КПД энергоаккумулирующих установок
|
|
Недогретые жидкости |
Вытеснение горячей воды |
Непосредственное аккумулирование питательной воды |
Изоляция, смешение, выравнивание температуры |
Неполный предварительный нагрев, закачивание |
Теплообмен или дросселирование, закачивание, изменение КПД турбоагрегата, повышение давления в конденсаторе Закачивание, изменение КПД турбоагрегата, повышение давления в конденсаторе |
0,8—0,95 0,9-1,02 |
0,7-0,9 0,8-0,95 |
|
Высококи- пящие жидкости |
Косвенное аккумулирование Непосредственное без - насосное аккумулирование тепла первичного цикла |
Изоляция, поте - тери нагрева и охлаждения мно - гососудных систем |
Теплообмен, закачивание Закачивание |
Теплообмен, закачивание, изменение КПД турбоагрегата, повышение давления в конденсаторе Теплообмен, изменение КПД турбоагрегата, повышение давления в конденсаторе |
0,75—0,85 0,9—0,97 |
0,6—0,75 0,08-0,95 |
|
|
Твердые тела |
Косвенное безнасосное аккумулиро вание |
Изоляция, выравнивание температуры |
Падение давления, теплообмен, закачивание |
Падение давления, теплообмен, закачивание, изменение КПД турбоагрегата |
0,8—0,85 0,75—0,8 |
0,7—0,75 0,6-0,65 |
|
|
Теплота фазового перехода |
Изоляция, недо - грев |
||||||
|
Термохимическое аккумулирование |
Гистерезис зарядки/разрядки |
Падение давления,, теплообмен, закачивание, охлаждение, конденсация или сжатие продуктов реакция |
Падение давления, теплообмен, закачивание, нагрев, испарение или дросселирование продуктов реакции |
0,7—0,74 |
0,5—0,55 |
|
Энерго аккумулирующие установки |
Эксергетические потери |
Эксерге- тический |
КПД |
||||
|
Аккумулирования |
в системе |
кпд разрядки |
аккумули рования |
||||
|
' |
аккумулятора |
аккумулирования |
Зарядка |
Разрядка |
|||
|
Гидростатическое давление |
Гидравлическое насосное аккумулирование |
Утечки, испарение |
Двигатель, закачивание, падение давления |
Падение давления, турбина, генератор |
0 1 о 00 |
0,5—0.75 |
|
|
Скользящее давление |
Пневматическое насосное аккумулирование |
Охлаждение, утечки, конденсация влаги |
Двигатель, компрессор, падение давления, дросселирование, охлаждение |
Дросселирование, падение давления, турбина, генератор |
0 82 |
0,65 |
|
|
X >» к со О ш |
Постоянное давление |
Двигатель, компрессор, падение давления, охлаждение |
Падение давления, турбина, генератор |
0,84 |
0,7 |
||
|
>s 3 н сс * и |
Скользящее давление |
Газотурбинное насосное аккумулирование |
Двигатель, компрессор, падение давления, дросселирование, охлаждение |
Дросселирование, падение давления, турбина, изменение потерь при сгорании и в градирне, генератор |
0,55* |
||
|
Постоянное давление |
Двигатель, компрессор, падение давления, охлаждение |
Падение давления, изменение потерь при сгорании и в градирне, генератор |
0,58 * |
|
* См. разд. 73.2. |
Полный КПД систем с косвенным аккумулированием ниже. Аккумулирование посредством теплоты горячих теплоносителей может быть предпочтительнее аккумулирования с использованием теплоты фазового перехода, где для организации теплообмена рабочего тела и аккумулирующей среды требуется дорогое оборудование и возникают эксергети - ческие потери. Постоянная температура аккумулирования является преимуществом только для паровых процессов; для газотурбинных процессов она становится недостатком. Термохимическое аккумулирование характеризуется сравнительно низкими КПД, но его преимуществом является отсутствие потерь в изоляции и, следовательно, неизменность КПД в течение длительных промежутков времени (сезонное аккумулирование). Могла бы представлять интерес система прямого термохимического аккумулирования.
Полный КПД насосных систем аккумулирования низок из-за того, что он зависит от семи частных КПД (при этом гидравлические системы предпочтительнее пневматических). В пневматических системах аккумулирования с постоянным давлением отсутствуют потери на дросселирование во время зарядки и разрядки. Полный КПД систем аккумулирования, использующих тепловые насосы и аккумуляторы со скользящим давлением, снижается вследствие изменений давления в верхнем и нижнем аккумулирующих сосудах и соответствующих потерь в компрессоре и турбине.
Из табл. 3.1 следует, что вообще т]ак традиционных тепловых систем аккумулирования выше, чем у более новых термохимических и пневматических систем, а также у систем, основанных на использовании теплоты фазового перехода и принципа теплового насоса. Разница может быть скомпенсирована только значительно более низкими начальными затратами на сооружение новых систем.