ТЕПЛОТЕХНИКА

ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ

При макрофизическом подходе к явлениям природы мы встре­чаемся со специфическими свойствами теплоты. Повседневный опыт дает основание утверждать, что невозможно возвращение какой-либо термодинамической системы (или рабочего тела) в первоначальное со­стояние без каких-либо изменений в окружающей ее среде. Первый закон термодинамики, утверждая взаимопревращаемость теплоты и работы, не ставит каких-либо ограничений в осуществлении этого процесса. Между тем повседневный опыт учит нас, что если превра­щение работы в теплоту не связано с какими-либо ограничениями, то обратный процесс — превращение теплоты в работу — требует для своего осуществления определенных условий. Первому закону термо­динамики не противоречит существование вечного двигателя второго рода, т. е. такой машины, в которой внутренняя энергия, переданная рабочему телу в форме теплоты, полностью превращалась бы в работу. Такой двигатель позволил бы практически неограниченное коли­чество внутренней энергии окружающей нас атмосферы, водных бассей­нов и земной коры превратить в работу. Однако создание такого двигателя невозможно не только практически, но и теоретически. Эти особенности теплоты, не противоречащие первому закону термодинами­ки, должны быть постулированы отдельно. Широкое обобщение осо­бенностей теплоты как формы передачи внутренней энергии от одного объекта к другому, обнаруживаемых при макрофизическом подходе к явлениям природы, и составляет содержание второго закона термоди­намики.

Необратимость процессов является одним из вопросов, рассматри­ваемых при анализе второго закона термодинамики. Результаты термо­динамических расчетов, без учета необратимости реально протекающих процессов, не согласуются с опытом, и поэтому, чтобы полнее вскрыть содержание второго закона термодинамики, необходимо обсудить вопрос о необратимости термодинамических процессов.

Необратимость термодинамических процессов. Рассмотрим термоди­намическую систему, состоящую из рабочего тела и окружающей среды. Из определения обратимого процесса (см. с. 8) следует, что в обратимом процессе при возвращении рабочего тела в первоначальное состояние оно должно проходить через те же промежуточные термодинамические состояния, которые оно проходило в прямом процессе. Если, например, при расширении газа в цилиндре от состояния 1 до 2 (рис. 1.32) он проходил промежуточные термодинамические состояния е и /, то при сжатии от состояния 2 до 1 он должен проходить те же промежуточные состояния, но в обратной последовательности, т. е. / и <?. Это возможно только в том случае, если процессы 1-2 и 2-1 обратимые. Однако в природе обратимых процессов не существует и для того чтобы рабочее тело перешло из одного равновесного состояния в другое, необходимо нарушить это состояние; в этом случае в рабочем теле возникнут возмущения в виде градиентов Ар/р, Ар/р и А Т/Т, на компенсацию которых будет затрачена часть энергии. В результате осуществления такого реального процесса в прямом и обратном направлениях рабочее тело придет в первоначальное состояние, но в системе про­изойдут изменения: часть энергии будет безвозвратно потеряна на компенсацию,, указанных возмущений или, как говорят, на компенсацию потерь энергии на необратимость. В самом деле, в обратимом процессе расширения газа на участке 1-2 работа расширения /Сг. равна работе сжатия Цв на участке 2-1, т. е. /g6 = пл. Ief2341 = пл. 2fel432 — Lco5 и, сле­довательно, в системе никаких изменений не произошло. В необрати­мом же процессе работа расширения газа на участке 1-2 lfip — пл. Idc2341 Меньше /gб иа величину АР = PoG - /БР = пл.leficdl, которая является поте­рей энергии на необратимость. В последующем процессе возвращения газа в первоначальное состояние затрачиваемая работа сжатия 1спр = = пл. 2bal 432 больше 1соб на величину А/с = /?,р - = wi.2balef2. Таким образом, при возвращении рабочего тела в первоначальное состояние в системе произошло изменение: в ней обнаружились потери энергии на необратимость иа величину fHp = АР + А/с = пл./Ablcd 1. Другими

Р

3 If

Рис. 1.32. Графическое толко­вание необратимости про­цесса в координатах р, V

Словами, в ней бесполезно передана газу энергия 1нр = Qlw, вследствие чего его энтропия возросла на

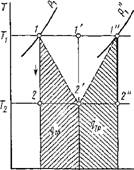
По этой же причине необратимый адиабатный процесс не может быть изоэнтропийным, что наглядно изображено на рис. 1.33. В конце необратимого адиабатного расширения от 7І до Т2 рабочее тело характе­ризуется состоянием 2', а не 2, так как в результате этого процесса вследствие потерь на необратимость возрастает энтропия. Если теперь осуществить необратимый процесс адиабатного сжатия до первоначаль­ной температуры, то и в этом случае по той же причине рабочее тело будет характеризоваться не точкой Г, а точкой 1", при этом работо­способность рабочего тела уменьшится, поскольку при температуре Ті давление уже будет р'{ < рл. Таким образом, при протекании в термо­динамической системе необратимого процесса неизменно возрастает энтропия и тем в большей степени, чем больше необратимость; сле­довательно, изменение энтропии является мерой необратимости тер - модинамических процессов.

Процесс теплообмена, т. е. передачи внутренней энергии в форме теплоты от тела с температурой Ті к телу с температурой Т2<Ти Также является процессом необратимым и протекает с возрастанием энтропии в системе. В самом деле, в этом процессе энтропия горячего тела уменьшается на величину Bq/Ti, а холодного, наоборот, увеличи­вается на величину 5Q/T2 и, следовательно, энтропия системы dsc = = dsi + ds, = -Bq/Tx + Bq/T2 = Bq{L/T2 - L/Ti) > 0, т. е. возрастает.

Все реальные процессы являются процессами необратимыми и все они протекают с потерей энергии на необратимость, т. е. с пониже­нием работоспособности и возрастанием энтропии системы. Необ­ратимость реальных процессов связана с потерей энергии на компенсацию градиентов параметров, характерных для данного процесса. Так необ­ратимость гидродинамических процессов (движение вязкой жидкости и газа по каналам, смешение и перемешивание этих рабочих тел и т. д.) связана с потерей энергии на компенсацию градиента давления; необ­ратимость массообменных процессов связана с потерей энергии на ком­пенсацию градиента концентрации и т. д.

В термодинамике принято внутренней называть необратимость, обусловленную потерей энергии на компенсацию градиентов парамет­ров в рабочем теле (Ар/р, А р/р, Д Т/Т), а также на трение потока о стенки канала. Все потери энергии на необратимость называют потерей на тре­ние, выражают их в форме теплоты или работы и обозначают Qrp и /тр. Внешней называют необратимость, обусловленную конечной раз­ностью температур в процессе теплообмена.

Из приведенного выше анализа следует, что любой реальный само­произвольный процесс является необратимым. Этот логический вывод из анализа протекания реальных процессов является наиболее общей формулировкой второго закона термодинамики.

Действительный процесс истечения. Рассмотрим действительный про­цесс истечения, т. е. с учетом внутренней необратимости. Считаем по-
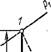
прежнему процесс истечения адиабатным, однако вследствие необрати­мости процесса энтропия потока увеличивается. В этом случае, как это показано на рис. 1.34, процесс истечения рабочего тела при изменении давления Or Pi до р2 изобразится условной кривоЙ 1-2д. ТАк как /і2Д > H2, То действительная Скорость иСтечения сд = ]/2(Hi — H2N) будет меньше теоретической с = ]/2 (Hi — H2) и поэтому можно написать, что

Сд = <рс, (1.179)

Где ф — так называемый скоростной коэффициент, значение которого меньше единицы. Экспериментально установлено, что для шлифованных и спрофилированных сопл ф = 0,95 ...0,98, а для цилиндрических со­вершенно необработанных насадок ~0,9.

Потеря энергии потока Д£ф на необратимость может быть выражена

Как

Д£тр = їЬІР£ї)1= СІЄ-ф2) (U80)

Величина (1 — ф2) называется коэффициентом потери энергии и обозначается греческой буквой С другой стороны,

- £Ц£к - IviF^R (1Ш)

Совмещая уравнения (1.180) и (1.181) между собой, получим 2

Откуда

H2д = H2 + (1 - Ф2) й- = H2 + (1.183)

Аналогично графику H, S на рис. 1.35 в координатах Т, S теоретический процесс адиабатного истечения изобразится прямой 1-2, а действитель­ный — условной кривой 1 -2д. Из этого графика видно, что площадь под кривой процесса 1-2д представляет собой теплоту с/гр, усваиваемую рабо­чим телом, вследствие чего его температура в конце процесса истечения Т2я будет больше температуры в конце обратимого процесса истече­ния Т2. Площадь под отрезком изобары 2-2д изображает потерю кинети­ческой энергии потока АЕтр из-за трения.

Найдем действительную температуру газа в конце адиабатного исте­чения Т2д. Так как /г2д - H2 = Qp - Cpm (Т2д — Т2), то, подставляя это выра­жение в уравнение (1.182), получим

(1-<р2) = срт(Т2л-Т2),

2

Откуда

Ъ+ -^-(1 - ф2). (1.184)

В координатах Т, S

Величина игд найдется для газов, подчиняющихся уравнению Менде­леева—Клапейрона, как ЯТщ/рг', для остальных газов и паров — по соответствующим таблицам для значений р2 и /ігд. Для водяных паров значение Via проще всего найти из /is-дйаграммы в точке р2, /ізД-

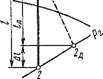
Действительный процесс в диффузоре. В необратимом процессе адиабатного сжатия рабочего тела в диффузоре от рХ до р2 процесс будет Происходить С ПОДВОДОМ К этому телу теплоты <2тр, вследствие чего энтропия его возрастает до значения S2Jx (рис. 1.36). В этом случае затрата работы в диффузоре на сжатие рабочего тела будет равна 'лиф = /дпф + <?тР + Ш1.122Ы. Дополнительная затрата работы, равная пл.122д1, как это видно из рис. 1.36 и 1.37, обусловлена тем, что вследствие Tin > 72 действительный удельный объем в конце сжатия 1>2д больше теоретического V2 и поэтому действительная кривая сжатия 1-2д в координатах р, V круче обратимой адиабаты 1-2. Таким образом, потеря энергии в диффузоре больше работы трения.

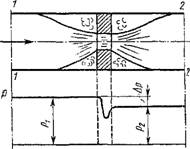
Дросселирование газов и паров. Если на пути потока имеется мест­ное сопротивление в виде резкого сужения проходного сечения (рис. 1.38), то при прохождении этого сечения давление рабочего тела понижается на величину Ар = Pi — р2. Процесс, в котором рабочее тело в результате прохождения местного сопротивления понижает свое давление без совершения работы или отвода теплоты, называется дросселированием. Это типичный необратимый процесс, и, следовательно, всегда сопро­вождается возрастанием энтропии. Рассматривая процесс дросселиро­вания без подвода теплоты извне в соответствии с рис. 1.38 и формулой (1.147), можно написать, что (с2 - Cj)/2 = Hx - H2. Обычно изменение ско­рости потока до и после местного сопротивления ничтожно мало, и им можно пренебречь. Очевидно, в этом случае H2 = Hx, т. е. в результате дросселирования энтальпия рабочего тела не изменяется.

Для идеального газа H2 — Hx = ср (Т2 - Тх) — 0, это означает, что для него Т2 = Тх, т. е. в результате дросселирования идеального газа его
температура не изменяется. У реальных газов и паров наблюдаются сле­дующие три случая: dT= 0; dT< 0 и dT> 0. Так как при дросселиро­вании во всех случаях dp < 0, то в общей зависимости

Dr=adp (1.185)

Значение dТ зависит от значения а — так называемого коэффициента адиабатного дросселирования, или дифференциального дроссель-эф­фекта. Явление изменения температуры при адиабатном дросселиро­вании называют эффектом Джоуля — Томсона. Значение а найдем сле­дующим образом. Подставляя в формулу (1.42) значение

Б Q = cpdT-

Получим

Dh = c„dT +

Рис. 1.36. Процессы обра­тимого и необратимого сжатия газа в диффузоре в координатах Т, S

Которое для случая дросселирования, т. е. при Dh — 0, можно переписать в виде

DT= v Jp----------------- dp. (1.187)

CP

Сравнивая формулы (1.185) и (1.187) между собой, получим

А = ----------------------------- . (U88)

Из формул (1.187) и (1.188) следует, что при T(dv/dT)p > v dT < 0, т. е. при дросселировании рабочее тело охлаждается; это явление называют положительным эффектом Джоуля — Томсона; при T(dv/dT)p < v dТ> О, т. е. при дросселировании рабочее тело нагревается (отрицательный эффект Джоуля — Томсона); и наконец, при T(dv/dT)p = v dT — 0, т. е. в результате дросселирования рабочее тело не меняет своей темпера­туры; эта температура называется температурой инверсии и обозначается Тинв. Следовательно,

Tum = v{dT/dv)p. (1.189)

Геометрическое место точек температур инверсии на рТ-диаграмме дает инверсионную кривую. Так как точки кривой инверсии удовлетво­ряются уравнением (1.189), то, используя его и уравнение состояния данного рабочего тела, можно построить для него инверсионную кри­вую. В качестве примера на рис. 1.39 приведена инверсионная кривая для азота. Во всей области, заключенной внутри инверсионной кривой, а > 0 и, следовательно, в ней при дросселировании азот будет охлаж­даться. Вне этой области а < 0 и поэтому здесь при дросселировании азот будет нагреваться. Таким образом, дросселирование газообразного азота при всех значениях начальной температуры Т< Tlim будет сопро­вождаться его охлаждением, а при Т> ТШІВ, наоборот, нагреванием. Поскольку для других рабочих тел кривые инверсии имеют аналогич­ный характер, можно утверждать, что для всех веществ, находящихся в газообразном состоянии, при Т< Тшв дросселирование сопровождает­ся охлаждением, а при Т> Тпп„ — нагреванием вещества. Если для дан­ного рабочего тела справедливо уравнение Ван дер Ваальса, то, как показывают соответствующие расчеты, в точке максимума инверсион­ной кривой итах = ук, Ртах = 9рк и Ттах = 37І-. Кривая инверсии при дав­лении р = 0 пересекается с осью температур в двух точках: слева — при Год = 0,75 Тк и справа — при Тол = 6,75 Тк. Значения Т0,2 для реальных газов хорошо согласуются с величиной 6,75 Тк при атмосферном давлении.

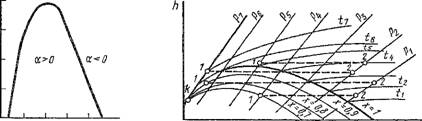
У водяного пара Тк = 647 К, и поэтому температура инверсии его должна быть равна примерно 4400 К. При этой температуре водяной пар полностью диссоциирован, и поэтому дросселирование водяного пара всегда сопровождается понижением его температуры. На рис. 1.40 представлены процессы дросселирования водяного пара различного состояния в координатах H, S. Эти процессы, как необратимые, проведены

P-10sПа

Рис. 1.40. Графическое изображение процесса дросселирования водяного пара в коорди­натах h, s

Условно пунктирными линиями. Из рисунка видно, что: 1) во всех случаях в результате дросселирования температура пара понижается; 2) влаж­ные пары невысокого давления при дросселировании подсушиваются и становятся перегретыми; 3) перегретые пары высокого давления остаются перегретыми после дросселирования; 4) влажные пары высо­кого давления при дросселировании сначала увлажняются, а затем подсушиваются, становясь перегретыми; 5) перегретые пары высокого давления и невысокой температуры перегрева при дросселировании сначала превращаются в сухой насыщенный пар, далее увлажняются, затем подсушиваются и снова становятся перегретыми, но низкого давления и температуры.

Теория циклов. Исторически второй закон термодинамики возник как рабочая гипотеза тепловой машины, устанавливающая условия прев­ращения теплоты в работу с точки зрения максимума этого превращения, т. е. получения максимального значения коэффициента полезного дей­ствия тепловой машины. Анализ второго закона термодинамики пока­зывает, что малая величина этого коэффициента является следствием не технического несовершенства тепловых машин, а особенностью теплоты, которая ставит определенные ограничения в отношении вели­чины его. Теоретически тепловые машины работают по круговым термодинамическим процессам, или циклам. Поэтому для того, чтобы шире раскрыть содержание второго закона термодинамики и провести детальный анализ его, необходимо исследовать эти круговые процессы.

Процесс, в котором рабочее тело, выйдя из некоторого начального состояния и претерпев ряд изменений, возвращается в то же состоя­ние, называется круговым процессом или циклом.

Для осуществления цикла необходимо наличие трех элементов: нагревателя или геплоприемника со средней температурой Ті, холодиль­ника со средней температурой Т2 <Т и рабочего тела, которое, последовательно вступая в теплообмен с нагревателем (или тепло - приемником) и холодильником, передает энергию от одного к другому. Как будет показано ниже, циклы бывают прямые и обратные, обрати­мые и необратимые.

Из определения цикла следует, что во всех без исключения циклах изменение в нем внутренней энергии, энтальпии и энтропии равно ну­лю. Отсюда следует, что первый закон термодинамики для циклов математически представляется в виде

«ц = /ц, (1.190)

Где Qn и U — алгебраическая сумма соответственно теплот и работ всех термодинамических процессов, из которых состоит цикл.

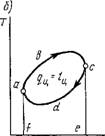
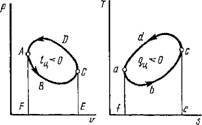
Прямой цикл есть цикл тепловой машины, в котором осу­ществляется превращение теплоты в работу. В координатах р, v этот процесс протекает в такой последовательности (рис. 1.41, а). На участке АБС рабочее тело, получая внутреннюю энергию в форме теплоты от нагревателя, совершает работу расширения H = Un.ABCEFA. После этого путем сжатия на участке CDA оно возвращается в первоначаль­ное состояние, причем часть полученной от нагревателя внутренней энергии в форме теплоты рабочее тело передает холодильнику. Работа сжатия 12 = пЛ-CDAFEC и, следовательно, работа цикла = H — 12 = — Wi.ABCDA > 0, поскольку по абсолютной величине положительная работа расширения рабочего тела h больше отрицательной работы сжатия 12. В координатах Т, S этот процесс протекает следующим образом (рис. 1.41, б). На участке Abc к рабочему телу подводится теп­лота из нагревателя qi = пл.Abcefa. Однако только часть этой теплоты превращается в работу, так как невозможно возвращение рабочего тела в первоначальное состояние без отвода от него в холодильнике в процессе сжатия части теплоты Q2, равной пл. Cdafea. Таким образом, количество теплоты, превращенной в цикле в работу (или, иначе, теплота цикла), будет

Qll = qx — q2 — пл. abcda > 0,

Поскольку количество теплоты <ji, подведенной к рабочему телу, боль­ше количества теплоты Q2, отведенной от него.

Таким образом, при анализе прямого цикла обнаруживается новое специфическое свойство теплоты: в круговом процессе теплота нагре­вателя не может быть полностью превращена в работу. Эта форму­лировка второго закона термодинамики принадлежит С. Карно.

В прямом цикле мы заинтересованы в том, чтобы максимум под­веденной к рабочему телу теплоты превратить в работу. Поэтому эффек­тивность прямого цикла оценивается отношением работы цикла /ц к количеству теплоты Qu подведенной к рабочему телу. Это отношение называют термическим коэффициентом полезного действия (к. п. д.) цикла и обозначают буквой г|,. Следовательно, термический к. п. д. прямого цикла

^-A.^-iL^-i-Ii.. (1.191)

4і Яі Яі Чх

Из рис. 1.41 и формулы (1.191) следует: невозможно создать тепло­вую машину, термический к. п. д. которой был бы равен единице. Этот вывод является другой формулировкой второго закона термодинамики, предложенной С. Карно.

Рис. 1.4.1. Графическое изображение прямого цикла в координатах /?, V И Т, S

Рис. 1.42. Графическое изображе­ние прямого цикла Карно в ко­ординатах р, V и Т, S

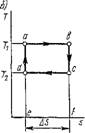
Идеальным циклом тепловой машины является прямой обратимый цикл Карно. Процесс в цикле Карно течет в такой последователь­ности (рис. 1.42). На участке Ab к рабочему телу подводится теплота Qx = ш. аЬ/еа = AsTi (рис, 1.42, б) из нагревателя при постоянной темпе­ратуре Ті, вследствие чего газ совершает на этом участке работу изотер­мического расширения It = пл. Abfea (рис. 1.42, а). На участке Be происхо­дит дальнейшее расширение газа, но уже адиабатно, за счет его внутрен­ней энергии. В последующем сжатии газа на участке Cd рабочее тело входит в соприкосновение с холодильником, куда от него отводится при постоянной температуре Т2 теплота Q2 = Im.Cdefc = AsT2 (рис. 1.42, Б). На участке Da происходит дальнейшее адиабатное сжатие газа, в ре­зультате чего рабочее тело возвращается в первоначальное состояние. В соответствии с первым законом термодинамики работа цикла Карно:

'ц — h — h — Qi — ch — пл - abeda = (Tj — Т2) As.

Подставляя выражения работы цикла и теплоты Q2 в формулу (1.191), получим

IiL_ M- _ 7 - Т2 ^ _ Т^

Т'

(1.193)

Ч

Из формулы (1.193) следует, что термический к. п. д. цикла Карно для газа не зависит от его природы и однозначно определяется темпе­ратурами нагревателя и холодильника. Нетрудно показать, что терми­ческий к. п. д. цикла Карно для вещества в любом физическом состоянии не зависит от его природы и определяется формулой (1.193). На рис. 1.43 в координатах Т, S изображены циклы Карно для двухфазной системы «твердое тело + жидкость», влажного и перегретого паров. Из этого рисунка видно, что для каждого из этих трех циклов работа цикла опре­деляется формулой (1.192) и, следовательно, термический к. п. д. - фор­мулой (1.193).

Необходимо иметь в виду, что выведенный нами термический к. п. д. цикла Карно относится к обратимому круговому процессу, состоящему из обратимых термодинамических процессов. Необратимость процесса связана с потерей работы, и поэтому термический к. п. д. необрати-
мого цикла Карно г)" всегда меньше обратимого т}", определяемого формулой (1.193). На рис. 1.44 условно изображен необратимый цикл ABCDA, в котором участки ВС и DA представляют соответственно необратимые адиабаты расширения и сжатия, протекающие с возраста­нием энтропии. Рабочее тело получает от нагревателя теплоту qi = = пл.АВМКА и отдает холодильнику теплоту q'{ = пл.CDNHC. В обрати­мом цикле Карно Q° = пл.FEKMF < q" и поэтому

(1.194)

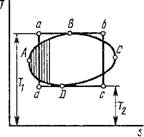
Докажем далее, что в заданном интервале температур 7 и Т2 об­ратимый цикл Карно обладает максимальным термическим к. п. д. по сравнению с любым произвольно взятым циклом. Для этого в заданном интервале температур 7 и Т2 рассмотрим два цикла (рис. 1.45): произвольный цикл ABCDA и цикл Карно Abcda. Оба цикла - прямые и обратимые. Проведя ряд адиабат, расположенных друг от друга на бесконечно малых расстояниях, разобьем цикл ABCDA на бесконечно болышое число элементарных циклов, состоящих каждый из двух адиабат и двух элементарных отрезков контура цикла ABCDA. Пренебрегая бесконечно малыми величинами высшего порядка, эти отрезки можно считать изотермами, и тогда эти элементарные циклы будут циклами Карно. Совокупное действие этих циклов одинаково с циклом ABCDA. Для всех элементарных циклов Карно Tu < Ті, а Т2І > Т2, и, следова­тельно, к. п. д. каждого элементарного цикла т^ = 1 — (Т^/Тн) будет меньше к. п. д. цикла Карно Abcda, равного г]к = 1 - (Тг/Тх). К. п. д. про­извольного цикла ABCDA равен среднему значению элементарных циклов Карно, к. п. д. которых каждого меньше к. п. д. цикла Карно Abcda. Следовательно, цикл Карно будет иметь больший к. п. д., нежели к. п. д. произвольного цикла ABCDA.

В заключение отметим три признака прямых циклов: 1) направление термодинамических процессов, из которых состоит цикл, в координа­тах р, v И Т, s — по часовой стрелке; 2) линия расширения в координатах

Р, V и линия процесса подвода теплоты в координатах Т, S должны быть выше линии сжатия и линии отвода теплоты в соответствующих коор­динатах; 3) алгебраическая сумма работ и теплот цикла больше нуля.

Обратный цикл есть круговой процесс холодильной машины и теплового насоса, в котором затрачивается работа извне для того, чтобы теплоту Q2 передать из холодильника в теплоприемник. Процесс осуществляется в такой последовательности. При расширении рабочего тела по линии ABC (рис. 1.46) к нему подводится количество теплоты Q2 от холодильника со средней температурой Т2. При последующем сжатии рабочего тела по линии CD А от него отводится в теплоприем­ник со средней температурой Тх > Т2 количество теплоты Qx, большее Q2. Таким образом, в обратном цикле теплота цикла Qlx = Qx — Q2 < О и работа цикла /ц = 1Х — 12 <0. Другими словами, в обратном цикле линия расширения ABC в координатах р, V и линия процесса подвода теплоты Abc в координатах Т, s лежат ниже линии CD А сжатия и Cda отвода теплоты. Другими признаками обратного цикла являются: 1) направле­ние процессов в цикле против часовой стрелки; 2) алгебраическая сумма работ и теплот цикла должна быть меньше нуля.

В обратном цикле, так же как и в прямом, Аи = 0 и, следовательно, для него первый закон термодинамики напишется так: — <?і = —/ц, где Q2, Qx и /„ — абсолютные величины. Отсюда следует, что

Qx=q2 + hb (1-195)

Т. е. отводимая рабочим телом в теплоприемник теплота равна сумме теплоты, полученной им из холодильника, и теплоты, эквивалентной работе, затраченной на осуществление цикла.

В машинах, работающих по обратному циклу, мы заинтересованы в минимальной затрате работы извне для передачи теплоты от менее нагретого тела к более нагретому. Поэтому эффективность обратного цикла оценивается отношением Q2 к /ц. Это отношение называют холо­дильным коэффициентом и обозначают буквой є:

Итак, осуществление обрат­ного цикла без затраты рабо­ты извне невозможно. Эта осо­бенность теплоты является од­ной из формулировок второго закона термодинамики, кото­рая гласит: теплота не мо­жет переходить от холодного тела к более нагретому сама собой даровым процессом (без компенсации). Эта формули­ровка принадлежит Ю. Клау - зиусу (1850). Одновременно с ним У. Томсон дал иную фор­мулировку второго закона, идентичную по содержанию, но отличную по форме: теплота наиболее холодного тела в данной системе не может служить источником работы.

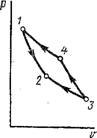
Идеальным циклом холодильной машины и теплового насоса является обратный обратимый цикл Карно, изображенный на рис. 1.47. Рабочее тело, которое в холодильной технике называется хладагентом, от началь­ного состояния 1 расширяется адиабатно на участке 1-2, причем темпе­ратура его падает от Г до Тх. Далее, по изотерме 2-3 оно расширяется, получая из холодильника с постоянной температурой Тх количество теплоты Q2. Затем на участке 3-4 происходит адиабатное сжатие хладаген­та, при котором температура его повышается от Тх до первоначальной температуры Т. На участке 4-1 происходит дальнейшее сжатие хладагента, но уже при постоянной температуре Т, вследствие чего он отдает тепло - приемнику с постоянной температурой Т количество теплоты Qx. В результате осуществления цикла на него была затрачена работа извне 1п = пл.12341, при этом от холодильника с температурой Тх получена теплота Q2, а теплоприемнику с температурой Т передана теплота Q{. Для цикла Карно холодильный коэффициент определится следующим образом (рис. 1.47):

_ Д2 _ Пл.23562__________________ AsTx __ Тх

S ~ Ш ~ Чг ~ Ші.41654 - пл.23562 ~ AST- AsTx ~ Т^7У

(1.197)

Аналитическое выражение второго закона термодинамики. Дадим аналитическое выражение второго закона термодинамики для обрати­мых и необратимых процессов.

Для обратимого цикла Карно можно написать, что - qK = 1 — Q2/Qi — = 1 - T2/Ti, откуда Q2/Qt = T2/Ti или Q2/T2 = QJT. Так как Q2 есть отводимое количество теплоты и, следовательно, его алгебраическое значение по смыслу отрицательно, то вместо Q2/T2 напишем { — Q2/T2). Тогда

I(g/T) = 0, (1.198)

Т. е. для обратимого цикла Карно алгебраическая сумма частных,

Полученных делением количества теплоты на абсолютную температуру, при которой эта теплота подводится или отводится, равна нулю.

Покажем, что это утверждение справедливо для любого обратимого кругового процесса. Как было показано выше, любой произвольно взятый цикл можно представить как сумму беско­нечно большого числа элементарных циклов Карно. Для каждого такого цикла J^(Bq/T) — О и, следовательно, для всего цикла ABCD А (см. рис. 1.45):

Ф (1.199)

J abcdЛ 1

Где §Abcda — интеграл, взятый по замкнутому контуру ABCD А.

Уравнение (1.199) называется интегралом Клаузиуса. Следовательно, для любого обратимого цикла интеграл Клаузиуса равен нулю.

Введем для подынтегральной функции интеграла Клаузиуса следую­щее обозначение: Bq/T = ds. Тогда уравнение (1.199) можно написать так:

§abcda DS = 0.

Из математики известно, что если криволинейный интеграл равен нулю, то дифференциал подынтегральной функции есть полный дифференциал. Следовательно, ds есть полный интеграл некоторой функции S. С термодинамической точки зрения функция S, изменение которой не зависит от процесса, а только от начального и конеч­ного состояний, есть параметр термодинамического состояния ве­щества и, как уже было показано выше, была названа Клаузиусом Энтропией.

Таким образом, для любого обратимого цикла можно напи­сать, что

Іавспа = §авспа Ds = 0, (1.200)

Или

5 Q = Tds. (1.201)

Уравнения (1.200) и (1.201) представляют собой аналитическое выражение второго закона термодинамики для обратимых процессов.

Для необратимого цикла Карно т]" = 1 — Q2/Qi < г|® = 1 — Т2/Ти Откуда следует, что — Q2/Qx < — Т2/Ти или Qz/T2> Qi/Tlt или

Ai- JLL. < о, т. е. Tt Т2

Любой произвольно взятый необратимый процесс ABCDA можно представить как сумму бесконечно большого числа элементарных не­обратимых циклов Карно, для каждого из которых ^(бд/Г) < 0, и поэтому для необратимого цикла ABCDA

Цг< 0. (1.202)

Abcda 1

З А. В. Чечеткин, Н. А. Заиемонец

Но для рабочего тела, совершающего цикл, <j>/1BaM ds = О и, следовательно,

5 Q

<ф ds = 0. (1.203)

Abcda * jabcda

Отсюда можно написать, что 8Q/T < ds, или необратимость процесса связана с увеличением энтропии по сравнению с обратимым.

Отсюда следует, что

8Q < Т ds. (1.204)

Уравнения (1.203) и (1.204) представляют собой аналитическое выражение второго закона термодинамики для необратимых про­цессов.

Свойство изолированной термодинамической системы. Физический смысл энтропии. Толкование второго закона термодинамики. Рассмотрим изолированную термодинамическую систему, состоящую из источника теплоты с температурой Ти холодильника с температурой Т2 < Тх И рабочего тела, которое совершает обратимый цикл Карно между источником теплоты и холодильником. В этом случае максимальная работоспособность системы равна

Ьі = біЛк = Qi (1 — Тг/Ті).

Количество теплоты, которое будет передано в холодильник рабо­чим телом,

Qz = Qi - Li = бі - Qi [1 - т2/т^ = Q, (Т2/Тх).

Изменение энтропии рассматриваемой системы будет равно алгебраи­ческой сумме уменьшения энтропии источника теплоты ASi = —QxjTx и увеличения энтропии холодильника As2 = Q2/T2, т. е.

AS = AS1 + AS2= --Q+-+ -

12 Тх т2 Тг Тх Т2

Теперь представим, что Qt источника теплоты сначала передается промежуточному телу, имеющему температуру Т < Тх. Тогда энтропия источника теплоты уменьшится на величину As І = — Qx/Tx, а энтропия промежуточного тела увеличится на As2 = Qi/T. В этом случае энтропия рассматриваемой системы вследствие протекания в ней не­обратимого процесса теплообмена между источником теплоты и про­межуточным телом возрастает на величину

AsIieo6p = As! + AS2 = — ~~ + (1.205)

После этого теплообмена источником теплоты в рассматриваемой системе будет промежуточное тело с температурой Т. Если теперь осуществить обратимый цикл Карно между этим телом и холодиль­ником, то получим максимальную работоспособность системы

Тг

L2 = QX4K = Q1[ 1

Уменьшение работоспособности системы AL вследствие протекания в ней необратимого процесса теплообмена составит

AL= L, - L2. а, (і - _ е, (t _ = fil І-) г2.

(1.206)

Сопоставляя между собой выражения (1.205) и (1.206), можно написать:

AL = Т2 As,.собр. (1.207)

Это уравнение называется уравнением Ги — Стодолы. Таким образом, Уменьшение работоспособности изолированной термодинамической систе­мы (вследствие протекания в ней необратимых процессов), т. е. дегра­дация энергии в этой системе, пропорционально увеличению в ней энтропии. Другими словами, энтропия является мерой деградации энергии в изолированных термодинамических системах. Энергия систе­мы, оставаясь неизменной количественно (в вышерассмотреииом случае Qt = Const), ухудшается качественно, переходя в теплоту низкого температурного потенциала.

Второй закон термодинамики по существу является статическим законом, характеризующим необратимость процессов, протекающих в конечных изолированных системах, и определяющим преобладающее направление макроскопических процессов, т. е. процессов, протекающих в системах с весьма большим числом молекул.

Этот закон неприменим к отдельным молекулам или к малому числу их. Нельзя сказать, что в этом случае он неверен, так как­ой вообще ничего не говорит по поводу поведения отдельной молекулы или малого числа их, ничего не утверждает по той причине, что к отдельной молекуле неприменимо понятие теплоты, ибо понятие это, равно как понятия температуры и энтропии, имеет смысл только по отношению к весьма большому количеству молекул. Это вытекает из феноменологического метода, который положен в основу термодинамики. Феноменологический метод заключается в том, что рабочее тело рассматривают не как дискретное физическое тело, состоящее из отдельных молекул, а как некоторый континуум, т. е. как сплошную среду, физические параметры которой непрерывны и из­меняются на бесконечно малую величину при переходе от одной точки пространства к другой. Это дает возможность изучать совокуп­ность действия молекул, проявляющуюся в том, что нами названо параметрами состояния рабочего тела. Так, совокупность импуль­сов всех молекул газа дает параметр давления; совокупность кинети­ческих энергий молекул — внутреннюю энергию газа, совокупность объемов, занимаемых молекулами в их движении, — удельный объем газа. Статистический метод является лишь дополнением к феноменологи­ческому методу и дает свои поправки в тех случаях, когда возможно судить о закономерности поведения отдельных молекул. Примером таких поправок является уравнение состояния реального газа.

Феноменологический метод применим только к системам, состоящим из большого числа молекул.

3*