ПОКАЗАТЕЛИ НАДЕЖНОСТИ ТЕПЛОВЫХ СЕТЕЙ
Выведем показатель надежности тепловой сети, представленной на рис. 10.1. Сеть состоит из трех участков, каждый из которых характеризуется своим значением параметра потока отказов соі. При отказе участка его отключают и часть потребителей лишается теплоснабжения.
|
Xj=(011) |
Так, например, при отказе участка 2 система недоподает 0,3 Q0 тепла, где Qo — расчетный расход тепла через систему. Неотключен - ные потребители, присоединенные к участкам 1 и 3, получают лимити-
Источник тепла
Xl = (101)
|
Сгг to Су > " Car |
|
<5г Н N с>Г |
|
—□ |
|
4j Xj = (no) |
|
Q- |
|
□-- |
Рис. 10.2. График состояний системы теплоснабжения
|
ТХЬ |
-схн
Гт
Рис. ГОЛ. Схема тепловой сети
|
ТАБЛИЦА 10.1. СОСТОЯНИЕ СИСТЕМЫ ТЕПЛОСНАБЖЕНИЯ
|
Рованное количество тепла и в отказовом состоянии находится не будут.
Рассмотрим возможные состояния системы, связанные с отказами участков теплопроводов. В целях упрощения отказы задвижек учитывать не будем. Вектор состояний системы будет иметь вид:
|
(0 |
||
|
X (0 = |
(0 |
|
|
(0 |
Транспонировав вектор-столбец X в вектор-строку Хт напишем граф состояний системы (рис. 10.2). Считаем, что во время ремонта одного элемента вероятность отказа другого ничтожно мала, поэтому возможны только четыре состояния: система исправна, т. е. XI = (111), или у системы отказал один из участков.
Каждому состоянию системы X (t) противопоставляем характеристику качества функционирования Фх {і). Для систем теплоснабжения она будет равна расчетному расходу теплоносителя за вычетом недоподачи тепла:
Qj it) = Qo — A Qf (t),
Где / — аварийное состояние.
Составим табл. 10.1 состояний систем, расположив их в порядке невозрастания характеристики качества функционирования.
Переходы системы из исправного состояния в отказовое характеризуются значениями параметра потока отказов соь сог и ю3. В результате ремонта система из состояния отказа возвращается в исправное состояние. Но, имея в виду социальное значение отказа системы теплоснабжения, оцениваем ее как неремонтируемую. Считаем, что при отказе система не выполнила задачу и остается в отказовом состоянии, т. е. переход системы из состояния отказа в работоспособное состояние невозможен. Такой подход ужесточает оценку надежности системы.
Таким образом, система может быть в двух состояниях: в исправном с вероятностью Рі (>t) и в состоянии отказа с вероятностью Рк (t). При этом возможны переходы системы только из исправного состояния в отказовое. Вероятность такого перехода за промежуток dt равна сOidt. Отметим на графе состояний (см. рис. 10.2) против каждой стрелки параметры потока отказов со*.
Переходные вероятности из исправного состояния в состояние отказа равны:
PZk = оо/ dt = dt. (Ю.8)
Вероятность остаться системе в исправном состоянии (не совершив за время dt ни одного перехода) определяется как вероятность события, дополнительного к совокупности всех возможных переходов из исправного состояния в отказовое, т. е.:
(10.9)
(10.10)
(10.11)
Свяжем вероятность состояния системы в момент t - f - dt с вероятностью ее состояния в момент t и переходными вероятностями. Если в момент t система находилась в исправном состоянии с вероятностью Pi (t), то за время dt она могла перейти в состояние отказа или остаться в исправном состоянии, не совершив ни одного перехода.
|
(10.12) |
Вероятность первого события — перехода системы за время dt из исправного состояния в отказовое—будет равна:
2 H <*> ®t* dt>
Где dt—условная вероятность перехода из состояния £ в состояние k при условии, что система находилась в состоянии
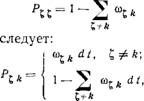
|
Из изложенного |
|
Dt. |
Вероятность второго события, когда система за время dt остается в исправном состоянии, £ будет равна
|
2> |
|
(10.13) |
|
Dt |
|
Tk |
Рг (0 1
В момент t система могла находиться в состоянии отказа с вероятностью Ph (0- Мы считаем систему неремонтируемой, поэтому, если система находится в состоянии отказа, то за время dt она не может совершить никакого перехода и с вероятностью в единицу остается в отказовом состоянии.
Теперь можно написать вероятности состояния системы в момент t - f dt. Вероятности нахождения системы в исправном состоянии в момент t -+- dt соответствует случай, когда она в момент t была исправна и за время dt не вышла из этого состояния, следовательно:
|
Dt |
|
(10.14) |
|
U |
Pt (t + dt) = Pt (t) 1
Вероятность нахождения системы в момент t dt в состоянии отказа равна сумме вероятностей: а) находиться в момент t в состоянии отказа и за время dt не выйти из него. Условная вероятность не покинуть состояния отказа равна единице; б) быть в момент t в исправном состоянии и за время dt перейти в состояние отказа.
Таким образом, вероятность Ph ~ (t - f dt) равна
Pk (t + dt) = Pk (о 1 +2 h W dt• (10Л5)
L+k
|
Момент |
Уравнения (10.14) и (10.15) составляют полную систему уравнений, определяющую состояние системы теплоснабжения в t -+- dt. Преобразуем эту систему следующим образом:
Pt (t + dt)-pl (О
Dt
|
DPz (t) Dt DPk (0 dt |
|
(10.16) |
Pk (t+dt)-Pk (О dt
= (0 2 t+k
Где k = 0, 1, 2, ..., т. е. уравнения записываются для всех состояний системы
Дл я решения системы дифференциальных уравнений необходимо задать начальное условие в виде вероятности (0) состояния системы теплоснабжения в начальный момент t = 0.
Напишем систему уравнений для рассматриваемого примера. Состоянию £ соответствует состояние 0, состоянию k — состояния 1, 2 м 3:
Р'о (0 =-Ро (о (соі + соз + соз); ] Р[ (t) = P0 (0 ал; Р'2 (t) = P0 (0 со2; ^з (0 = ро (0 «е.