ТЕПЛОПЕРЕДАЧА В СТРОИТЕЛЬСТВЕ

УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ ТЕПЛОТЫ ЧЕРЕЗ СТРОИТЕЛЬНЫЕ ОГРАЖДЕНИЯ

Глава 1

ОСНОВНЫЕ ФОРМУЛЫ И КОЭФИЦНЕНТЫ

»

Теплопроводность

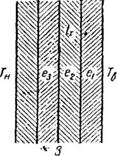
1. Возьмем строительное ограждение нз однородного материала, например в виде вертикальной стены, представленной на рис. 1. Если под влиянием прилегающей среды (например воздуха) на одной ее поверхности держится температура tn (в градусах Цельсия), а на другой то по закону физики (Фурье) количество теплоты, про­ходящей через стену в единицу времени' (1 час), пропорционально площади стены и разности двух ука­занных температур ее поверхностей и обратно про­порционально ее толщине. Обозначив площадь в квад­ратных метрах через F, толщину в погонных метрах через е и коэфициент пропорциональности через имеем для количества Q — проходящей через стену теплоты (в шал):

А [1]

1

Представим себе, что данная стена разделена на слои равной толщины Длг. Пусть Д/„ Д(2, Д/3 и т. д. Рис. J.

будут разности температур на двух разделительных плоскостях каждого из слоев: первого, второго и т. д.- Тогда, приняв во внимание, что при установившемся режиме через каждый слой проходит в 1 час то же количество теплоты, как и через всю стену, получим:

—1„ Л/.

IF—--------

е Ах

из чего заключаем, во-первых, что Д(1 = Д(2 = ... и затем что линия,

выражающая высоту температур во всех слоях плиты и на ее поверх­ностях, есть наклонная прямая:

At dt

— —- — const.

Ах dx

Таким образом характерной особенностью рассматриваемого типа движения теплоты является то, что помимо неизменяемости внутренних температур стены во времени нх диаграмма по ее толщине с пред­ставляет собою наклонную прямую.

Приняв в уравнении (1) F — 1 ж2, с= I м и /„ — — 1°, имеем

), = <2; таким образом коэфициеит пропорциональности ). представляет собою количество теплоты, которое стена из данного материала спо­собна пропустить через 1 м'~ своей площади в 1 час при разности температур на ограничивающих поверхностях в 1° и при толщине стены 1 м. Эта величина называется коэфициеитом теплопро­водности материала стены; подробнее о нем будет сказано ниже в связи с другими коэфициентами.

2. В предыдущем мы предполагали, что температуры обеих поверх­ностей стены tB и ta известны. Между тем в строительной практике обычно бывают известны не эти температуры поверхностей, а лишь температуры спеды, прилегающей к той и к другой поверхности, т. е. температуры воздуха внутри помещения и вне его.

Обозначив их соответственно через Тп и 7'„, выведем закон пере­дачи теплоты через ту же стену, исходя из этих величин.

Очевидно, в данном случае кроме прохождения теплоты через массу стены надо учесть процесс перехода ее от внутреннего воздуха на внутреннюю поверхность стены и затем переход от внешней поверх­ности стены к наружному воздуху. Пэ закону физики (Ньютона) количество переходящей таким образом теплоты при каждой поверх­ности в 1 час пропорционально площади стены и разности темпера­тур поверхности и среды (воздуха).

Обозначив коэфициенты пропорциональности соответственно через ап и а„ и приняв во внимание, что в обоих процессах проходит в 1 час одно н то же количество теплоты Q, имеем:

Q = auF (Тв — ta) = a„F (tu — Ttt). (2)

Величина ав есть так называемый коэфициеит тепловосприятия от среды (воздуха) к поверхности стены, а величина аи — коэфициеит теплоотдачи от поверхности стенок среде (наружному воздуху); тот и другой означают количество теплообмена в 1 час на 1 м2 поверх­ности стены при разности температур между поверхностью и средой в 1СЦ.

Взяв уравнения (1) и (2) совместно, представим их в следующем виде:

Q-~r^FV» — *н),

Q-~ = F(TB — tB

Q • — F(t„~ 7',,).

О = *7 1------------------------ г-р(7°— Tu) = k-F(TB — Тв), (3)

V+^-+„n

где

1 (4)

Из этого видно, что общая теплопередача через степу также про­порциональна ее площади н разности температур воздуха по обе ее стороны, но коэфициент этой пропорциональности k отличается от всех предыдущих н пыражается через них по уравнению (4). Он назы­вается коэфициентом общей теплопередачи через данную конструкцию (стену) и означает, очевидно, то количество теплоты, которое проходит через 1 м2 стены (от воздуха к воздуху) в 1 час времени при разности температур в обеих зонах воздуха в 1°.

3. Величины, обратные всем указанным коэфициентам X, ав, <*н, k, носят обычно название термических сопротивлений. Такие вели­чины— —, - І-, у — означают, очевидно, время (в часах), необходимое

в соответствующем процессе для передачи 1 ккпл теплоты через 1 м2 и при Дг — 1°, т. е. нечто противоположное способности (проведения теплоты), выражаемой коэфицнентами k, а, X. В частности величина

у = 8 [уравнение (1)], выражающая, очевидно, коэфициент теплопро­водности (не материала, а слоя) из данного материала толщиной е, будет иметь в качестве обратной сопротивление этой теплопровод­ности в слое, т. е. у или у. Такие определения, правильные и

по существу дела, находят себе наглядное подтверждение в уравнении (4), если перепишем его в следующем виде:

1 * • 1 _1_ 1

¥ = ТТ-^ + --- (5)

Это значит, что общее сопротивление потоку теплоты через конструк­цию в целом равно сумме сопротивлений по отдельным составляющим элементам этой конструкции—двум поверхностям и внутреннему мате­риалу. Это обстоятельство дает чрезвычайные удобства при расчетах теплопроводности ограждений, позволяя легко учитывать роль каждой части их в общем сопротивлении, „набирать" общее термическое сопротивление из его частей и т. п., как это будет видно в последую­щем изложении.

После всего вышеизложенного применение уравнений (3) и (4) к обыч­ным расчетам теплопотерь в практике становится понятным. Тем не менее некоторые более сложные случаи подобных расчетов должны быть рассмотрены здесь отдельно. Важнейшим из таких случаев является расчет теплопроводности ограждения, состоящего из несколь­ких слоев разных материалов (рис. 2).

4. Если все упомянутые слои состоят из твердых тел (в плотном или же рыхлом, сыпучем состоянии), то расчет теплопроводности такой системы мало отличается от выясненного выше. Пользуясь только что рассмотренным законом сопротивлений [уравнение (5)], можем уста­новить, что в формулу (4) для теплопередачи отдельные слои кон­

струкции будут входить совершенно так, как входит единственный

слой однородной стены, г. е. в виде членов типа у (сопротивлений

д теплопроводности); разница будет лишь в том,

что вместо одного слоя (всей прежней стены) с характеристиками с и X будет ряд слоев

с соответствующими им характеристиками е,

и Хр е, и Х2 и т. д. Таким образом для этих

случаев имеем формулу:

Т = ^+-^+Г+Г + ---+Т’

R “б “u 'і 2 'n

из которой найденное к используем для урав­нения (3).

5. Не представляет больших затруднений и Рис. 2. определение температур, создающихся внутри

составной стены, например в разделительных плоскостях между слоями. Для этого определения нами может быть использован уже упоминавшийся ранее принцип равенства количеств теплоты, проходящих в единицу времени (I час) через всю толщину стены и через какую-либо часть ее за то же время. Пусть например требуется определить температуру tx в разделительной плоскости АВ применив указанный принцип, имеем:

SHAPE * MERGEFORMAT

1 ііі’Дц/2 , ,еп а. + а„ + А, + X, +•••+ X.,

k. F(TB-TK) = k, F(TK-tx);

t —Т -

а: в

Для Поверхности стенки имеем, очевидно: для внутренне» k., — a и для наружной

1

1’ ij ■

— - L iL - L fK 4.Л4.ІІ

п 1 і * * * * »

Как видим, коэфициеит k2 есть частный коэфициеит теплопередачи от внутреннего воздуха к сечению, в котором ищется температура.

Для стены в 2,5 кирпича при 7^ = -]-20°, Ти~ — 30°, е —0,64 м, X = 0,7, ав == 7,5 и а„ = 15, получим:

t =20 — 5,85 = 14,15°, t = 20 — 46,85:

Аналогично поступаем и при многослойных стенах.

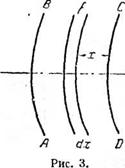
6. Рассмотрим тот же вопрос о теплопередаче стенок в более общем виде — для ограждения с произвольным очертанием поверхно­стей. Пусть имеем поверхности АП и CD (рис. 3), из которых первая воспринимает теплоту, а вторая отдает ее. Со­храняя прежние обозначения и называя через FB и F площади поверхностей на 1 йог. я их длины, нормальной к плоскости чертежа, имеем для установившегося теплового состояния стенки (равенства входа и выхода теплоты) уравнение:

Q = WTB-tB) = Fa(ta-TB),

t т Q и і —т і О

ти +

Возьмем теперь слой dx с поверхностью / в ограждении, находящейся в расстоянии х от поверхности CD и имеющей температуру t.

По общей теории теплопроводности имеем количество проходящей здесь теплоты на 1 ног. м:

Q — —ft'

откуда имеем падение температуры в слое

dt ~ —dx.

Интегрируем последнее равенство в пределах х = 0, х = е и t — tu, t = tB; тогда получим:

в и Л J /

О

Вставив сюда найденные выше выражения для tB и /н, имеем оконча­тельно:

тв~та Q =--- 5 !L—

1 rdx f

Для рассмотренного выше частного случая плоской стенки с парал­лельными сторонами следует принять:

тогда

х

dx г

T~~F’

О

f {Т — Г )

1 * В Н'

~Т Т р ’

J-4- —-1-4-

“и ^ к

7. Для цилиндрических труб с течением теплоты изнутри при вну­треннем и наружном диаметрах d и D имеем в общей формуле:

х = ^-~ и f=(d--2x)K.

Поэтому

п-а

2

TOC o "1-5" h z Г йх Г dx 1 . D

J ~f J (d + 2x)V ' 2n d

Qa= _______________________________ ■ (7)

4 1_ ,____ J, D_ ’ 1’

da„ + Da„ + 2X d

что дает нам формулу для расчета теплопотерь горячими трубами на 1 пог. м длины.

Представим ее в обычном виде:

Q = k(TB—Гв), причем, положив еще D — D0, имеем:

_1_ _ _1_____ .____ 1__ , _1_ Д)

k ~d'J-v _ r. D( aR "T~2irX" П d

Как видим, правая часть этого равенства представляет сумму тер­мических сопротивлений рассматриваемой теплопередачи — два на поверхностях трубы и одно в виде материального слоя стенки. Отсюда следует, что в случае многослойной стенки (с изоляцией) к указанной выше сумме термических сопротивлений прибавляются

-f УоЛ-In-

TOC o "1-5" h z 1 2 ял л 2 it).,, і

k Tirfa ~ л/)ма ' 2п). ,i XJ 2icXm Д„_, ' j

я=1

і

Таким образом для многослойном стенки будем иметь формулу: !

------------------------ -(Гв—4--------------------------------------------- (8)

А) . ^ і А.

+ огіп ->- + У«г-1п

rfaB Z)nan 2Х ’ d 2Х„

Если заданы не температуры среды (внутренней и внешней), а тем­пературы обеих поверхностей стенки, то в формулах (7) и (8) отпа­дут дроби, содержащие aD и an (так как указанное условие равносильно заданию a = оо = a ). Подобным же образом поступаем, если одна из заданных температур относится к поверхности стенки, а другая к среде.

8. При изоляции труб часто бывает нужно определять темпера­туры в разных разделительных поверхностях между слоями изоляции, например для проверки какого-либо слоя на перегрев, возгорание или плавление (гудрона). В этом случае поступаем совершенно аналогично тому, как и при плоской стенке, т. е. приравниваем:

Q — k(TB 7^) = ft, ( Гв х),

где х — искомая температура разделительного слоя;

ft —коэфициеит теплопередачи всей стенки и

ft,— лишь той части, которая расположена между внутренней сре­дой и данной разделительной поверхностью; - оба эти коэфн - циеита определяются, как было указано выше.

Утолщение изоляции, с одной стороны, уменьшает внутреннюю теплопроводность стенки, а с другой — увеличивает теплоотдающую внешнюю поверхность. Поэтому такое утолщение не всегда выгодно в смысле уменьшения теплопотерн. Возьмем случай с одним изоляцион­ным слоем, т. е. положим в формуле (8) и = 1. Наименьшая или наи­большая теплопотеря Q будет, очевидно, в том случае, когда знаме­натель правой части достигает максимума или минимума. Приравняв нулю производную этого знаменателя по D., получим:

TOC o "1-5" h z і_____ 1

2>-А V?

или

1 1

= 0,

2Х, аЛ откуда

D,=^.

ан

Так как вторая производная левой части предыдущего уравнения дает нам величину "Г-rj всегда положительную, то, очевидно,' при г, 2Х,

Dl мы имеем дело с минималЬным значением знаменателя и сле­
довательно с максимальным значением теплоиотери Q. Таким образом при толщине изоляции, равной е = ~ — —, и при близких к ней мы

“н [2]

имеем худшие условия изоляции. Из последнего выражения легко видеть, когда преимущественно будут такие условия: при малом диа­метре основной трубы D0 будут опасны толстые изоляции (особенно при больших X,), при больших трубах — изоляция всегда выгодна *.

Уравнения (З) и (8) являются основными для тепловых расчетов при установившемся движении теплоты, в частности для расчетов теплопотерь отапливаемых помещений при проектировании системы их отопления, равным образом для расчетов внешнего нагревания охла­ждаемых помещений (холодильников, некоторых фабричных помещений при проектировании их искусственного охлаждения) и наконец для трубопроводов. Поэтому необходимые для применения этих уравне­ний коэфицненты, т. е. k и составляющие его X, ав и ан, должны быть рассмотрены более подробно.