Теплопередача и оконные заполнители
Конвективный теплообмен в межстекольном пространстве окон
Рассмотрим вертикальную замкнутую герметичную воздушную прослойку, причем ее высота Н намного превышает ее ширину L. Температуры на внутренних поверхностях прослойки равны t{ и І2 и будем считать, что они постоянны по высоте. Теплопередача в такой воздушной прослойке зависит от температур tj и t2 и относительной ширины прослойки H/L. Ограниченное пространство накладывает определенные особенности на теплообмен, заключающийся в том, что циркуляция воздуха в замкнутом пространстве возможна только при определенных физических условиях [35]. Режим течения в прослойке зависит от критерия Грасгофа GrL-g/3(t/-t2)L3/^.
По данным экспериментов [113] критическое число Грасгофа равно
щ
|
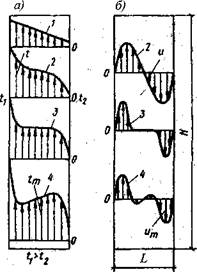
Рис.1.14. Развитие температурных (а) и скоростных (б) профилей в воздушной прослойке |
т
U/B g
Рис. 1.13. Профили скорости и температуры в пограничном слое около поверхности остекления
|
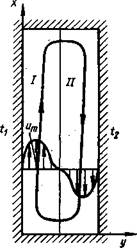
Рис. 1.16. Схема движения воздуха в замкнутой воздушной прослойке I - пристенный пограничный слой |
|
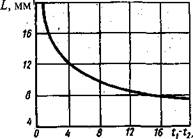
Рис. 1.15. Предельные значения ширины воздушной прослойки, при которых во всей полости отсутствует конвекция |
II - ядро течения
GrLKp=l400. Таким образом, при GrL < Grtp конвекция в прослойке отсутствует, передача тепла осуществляется только теплопроводностью и излучением, температура в прослойке изменяется по линейному закону (прямая 1 на рис.1.14). Приняв физические параметры воздуха при температуре 0°С, можно найти в зависимости от температурного перепада предельное значение ширины воздушной прослойки, при которой не происходит конвективного движения:
LKp<0,019(tj -12)'1/3 . (1.22)
На рис.1.15 приведены численные значения при различных перепадах
температур. При значении GV=1400, возникает ламинарная естественная конвекция. При Gri>Grip изменение температуры вдоль ширины прослойки отклоняется от линейного закона (кривые 2,3,4 на рис. 1.14). При этом в прослойке образуются два пограничных слоя [36]. Около стенки с большой температурой tj воздух движется вверх, а с меньшей t2 - вниз и профили скоростей у стенок имеют вид параболы (рис. 1.16). Ширина пристенного пограничного слоя растет сверху вниз у стенки с большей температурой t/ [21]. У стенки с меньшей температурой Ь наоборот. Рассмотрим два случая развития пограничных слоев у стенок.
Первый случай: ширина прослойки L велика. При этом около холодной и теплой стенок образуются независимо друг от друга свободноконвективные потоки воздуха, и взаимодействия их не наблюдается. Изменение скорости и температуры для такого случая показано на рис. 1.14 кривая 3. Локальные коэффициенты теплоотдачи можно рассчитывать по формулам (1.19) и (1.21), отсчитывая расстояние снизу вверх у теплой поверхности и наоборот у холодной. Здесь должно соблюдаться условие Sx+Sr >L, где Sx и 5т - толщина пограничных слоев, образующихся около теплой и холодной поверхностей остекления. Значения Зх и бт можно определить по формулам:
для ламинарного режима при Рг=$,1 [112]:
|
(1-24) |
|
для турбулентного режима [7]: |
3I/x=3,68Gr;i/6
Второй случай: пограничные слои взаимодействует друг с другом, т. е. дх+&г<Ь. Вследствие взаимодействия пограничных слоев, между ними возникают циркуляционные вихри [121]. Установлено, что при небольшой разности температур возникает одно циркуляционное движение, симметричное относительно центра прослойки. С увеличением перепада 0-ґ2 количество циркуляционных зон растет. Профили скоростей и температур в прослойке показаны на рис. 1.14 кривыми 2 и 4. Температурный профиль (кривая 2) говорит о том, что в центральной части ядра теплообмен происходит теплопроводностью (линейный участок распределения температуры).
Следует отметить, что температура в ядре прослойки не постоянна по высоте, а увеличивается снизу вверх. На рис. 1.17 в безразмерном виде нанесены экспериментальные данные [111], которые можно аппроксимировать кривой:
|
(1.25) |
(t - tj/(ti - t2)=0,83~ 0,6(x/L)
Характер развития пограничного слоя зависит не только от значения числа Грасгофа Gri, но и от отношения высоты прослойки к ее ширине Н/L. Анализ и обобщения опытных данных позволяют найти критическое число GrLKp:
|
(1.26) |
GrLKp=1 OO(WL)lJ.
Формула (1.26) получена для отношений H/L-5-40: при числе (7/у<1000 во всей воздушной прослойке отсутствует конвекция; при 1000<GrL<GrLKp конвекция существует в верхней и нижней частях воздушной прослойки, а в средней части она отсутствует; при Gr^Gr^ в воздушной прослойке наблю-
|
а)
|
|
trh |
|
Рис.1.17. Зависимость изменения температуры t„, в ядре прослойки (у/И=0,5) от х/Нпри trtr 19°С (1); 33°С (2); 46°С (3); 61 °С (4;) 75°С (5); 88°С (6) а) H/h = 20; б) H/h = 10 |
|
f |
Г |
|||
|
і |
Г |
|||
|
Xf и b |
|
л и to as в* я? |
|
б) |
|
о яг |
|
я* |
|
as |
to trt& t,-u
|
- |
||||
|
•А" |
.т1" |
|
Пил |
|
т 60 м. 20 Ю- ь к 7 |
Рис. 1.18. Зависимость Nuc от Grv (сплошной линией показаны расчеты по формуле (1.27), точками - опытные данные при i,-t2 от 5,5 до 88'С); H/h-20
|
■£gMtL
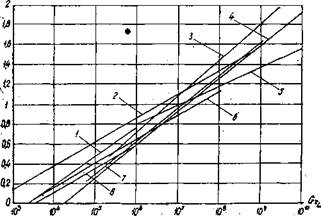
Рис. 1.19. Конвективный теплообмен в плоских вертикальных щеляхи прослойках по данным разных авторов: 1 - М. А. Михеев, A4=0,0947G/yw; 2 - Макгрегор, Р. Эмери, NuL=0,229GrLQ2S(H/Ly02 H/L= 1; 3 - Де Грааф, NuL=0,0317Gr/’A 4 - Макгрегор, Р. Эмери, 7'/wi=0,041Gri°’533; 5 - М. А. Михеев, NuL=Q,3&4GrL0'; 6 - Р. Эмери, П. Чу, Nu^OaSiGr^iH/L)4^; 7 - Д. Дропкин, Е. Соммерскейзл, NuL=0,0426Gr°’m; 8 - Макгрегор, Р. Эмери NuL=0,229GrLb'2H/LT'2i H/L=�. |
дается ламинарное конвективное движение.
Анализ экспериментальных и теоретических работ [108, 109, 114-124] показывает, что в интервале изменения критерия GrL от 103 до 107 существует ламинарный режим течения, при Grj> 107 - турбулентный. Ламинарный режим течения рассматривается в нескольких работах [43, 47, 60, 111], где приводится локальное распределение коэффициентов теплоотдачи вдоль высоты прослойки. Локальные коэффициенты теплоотдачи на теплой и холодной сторонах прослойки непостоянны по высоте, также как и при естественной конвекции у вертикальной поверхности они растут снизу вверх около холодной поверхности и падают около теплой стенки. На рис. 1.18 представлены результаты экспериментальных исследований [111] локальных коэффициентов теплопередачи для значения H/L=20. Температурные перепады при этом составляют /у-Ь=(5-88)°С. Экспериментальные точки, показанные на рис. 1.18, аппроксимируются зависимостью:
Nux=0,231Grx03 (1.27)
Уравнение (1.27) справедливо для теплой стенки. Координата х отсчитывается от нижней грани прослойки. Для расчета локальных коэффициентов на холодной поверхности необходимо координату х отсчитывать от верхней грани, а температурный напор в критерии Грасгофа следует брать tm-t2. На нагретой стенке локальные коэффициенты теплоотдачи уменьшаются с увеличением х.
Средний коэффициент теплоотдачи по толщине прослойки можно найти из уравнения (1.27) после интегрирования по х:
NuLcp = 0,119GrL0i(L/H) °'1. (1.28)
где Nulp=o£pL//I - критерий Нуссельта; аср - коэффициент теплопередаче в прослойке.
Соотношение (1.28) можно применять при 5<H/L<20 и 103<GrL<106. В
приближенных расчетах при значении 103<(лу<1010 и Н/Ь>5 М. А. Михеев [55] рекомендует использовать следующую зависимость:
NuLcp = 0,18(GrLPrf25 (1.29)
|
Коэффициенты С, А, т в формуле NuL~C(Gr[)A(H/L)'m |
Результаты работ разных авторов, исследовавших теплообмен конвекцией в плоских вертикальных щелях и прослойках, можно представить в виде таблицы, если Nui аппроксимировать зависимостью NuL=C(GrJA (H/L)'m. Данные о коэффициентах С, А, т [93] представлены в таблице 1.8, а часть зависимостей представлена на рис. 1.19.
|
Источник |
С |
А |
т |
H/L |
GrL |
Режим теплообмена |
|
М. А. Михеев |
0,0947 |
0,3 |
0 |
- |
1,5-103—1,5-106 |
ламинарный |
|
0,384 |
0,2 |
0 |
- |
1,5-Ю3-1,5-Ю10 |
турбулентный |
|
|
Мулль, Райер |
0,18 |
0,25 |
0,111 |
3-42 |
1,5 104-1,5 105 |
ламинарный |
|
0,065 |
0,333 |
0,111 |
3-42 |
1,5-105-8-106 |
турбулентный |
|
|
Макгрегор, Р. Эме |
0,229 |
0,25 |
0,25 |
2-40 |
2-Ю4 |
ламинарный |
|
ри |
0,381 |
0,25 |
0,3 |
1^10 |
1,5 Ю4—1,5 107 |
ламинарный |
|
0,041 |
0,333 |
0 |
1^10 |
1,5-107-1,5-109 |
турбулентный |
|
|
Д. Дропкин, Е. |
0,0426 |
0,333 |
0 |
4,4-16,6 |
7-104-109 |
турбулентный |
|
Соммерскейзл |
5-Ю3—106 |
|||||
|
В, И. Полежаев |
0,108 |
0,32 |
0 |
1-10 |
103—5-105 |
ламинарный |
|
Мунет, Диксбури |
0,2 |
0,263 |
0,21 |
1,25-20 |
103-108 |
ламинарный |
|
Р. Эмери, П. Чу |
0,258 |
0,25 |
0,25 |
- |
1U 1 v 103-5-106 |
ламинапрный |
|
Э. Эккерт, В. Карл |
0,119 |
0,3 |
0,1 |
2,3-46,7 |
ламинарный |
|
|
сон |
104-3 • 1 о5 |
|||||
|
Де Вааль Девис |
0,135 |
0,315 |
0,204 |
2,5-35 |
7-Ю5 |
ламинарный |
|
Де Грааф |
0,0317 |
0,37 |
0 |
19-63 |
JL* 1U 103-105 |
турбулентный |
|
М. Ньюэл, Ф. |
0,155 |
0,315 |
0,265 |
2-20 |
ламинарный |
|
|
Шмидт |
105-108 |
|||||
|
Ниман |
0,0236 |
0,393 |
0 |
- |
3,5-103—107 |
турбулентный |
|
Э. М. Литицкий, |
0,118 |
0,27 |
0 |
- |
переходный |
|
|
Э. А. Сидоров |
5-Ю6 |
|||||
|
Лэндис, Яновиц |
0,111 |
0,279 |
0 |
20 |
ламинарный |
|
|
Е. Польгаузен |
0,202 |
0,25 |
0,25 |
- |
ламинарный |
|
|
О. А. Саундерс |
0,0359 |
0,333 |
0 |
- |
турбулентный |
|
|
М. А. Михеев |
0,0539 |
0,333 |
0 |
- |
1,4-104 |
турбулентный |
|
Э. А. Сидоров |
0,0534 |
0,333 |
0 |
18-96 |
турбулентный |
|
Таблица 1.8 |
Анализ приведенных зависимостей показывает, что в области ламинарного режима течения и теплообмена некоторые авторы указывают на зависимость Nu от критерия H/L в степени -0,25. Таким образом, если свободная конвекция происходит в вертикальной плоской прослойке, то формирование и развитие ламинарного пограничного слоя, а следовательно, и теплопередача конвекцией определяется, помимо величины GrL, еще и величиной Н.
В случае вертикальной прослойки, ограниченной снизу и сверху (герметичной), вблизи верхнего основания происходит переход от подъемного движения к опускному, а вблизи нижнего - от опускного к подъемному. Это приводит к образованию вверху и внизу прослойки зон поперечных течений воздуха, которые интенсифицируют процесс теплообмена. С уменьшением величины H/L зоны поперечных течений занимают все большую часть общего объема прослойки, благодаря чему увеличивается среднее значение NuL. Очевидно, что при большом значении параметра H/L влияние концевых зон на NuL уменьшается.
Некоторые авторы отмечают, что граница перехода от режима теплопроводности к ламинарному теплообмену Gripl будет зависеть и от параметра H/L, так согласно Эккерту и Дрейку, определяется выражением:
GrLKpl=124Pr7(Pr+20/21)H/L (1.30)
При Pr=0,7 Gripi=409H/L.
Относительно границы перехода от ламинарного режима к турбулентному Grtp2 единого мнения нет. Согласно данным различных авторов, эта величина колеблется в очень широких пределах. Это связано с тем, что кроме L, At еще влияет и высота прослойки Н. Для вертикальной пластины Саундерсом в качестве Grip2 предложено выражение Grip2-109(///L)'3. Аналогичные зависимости, выведенные на основании экспериментальных данных и численных расчетов разных авторов, получены также В. И. Полежаевым и Бэтчелором.