Теплонспользующие установки промышленных предприятий

Полный факторный эксперимент

Каждый фактор в опыте может принимать одно или несколько значений. Такие значения будем называть уров­нями. Фиксированный набор уровней факторов определяет одно - из возможных состояний объекта. Это и есть условия проведе­ния одного из возможных о. пытов. Если перебрать все воз­можное множество различных состояний факторов, то мы по­лучим полное множество состояний объекта.

Чтобы узнать число различных состояний, достаточно число уровней факторов (если оно одинаково для всех факторов) возвести в степень числа факторов.

Так, если Р — число уровнений и /г — количество факторов, тс число различных состояний /V = Рк (15.1). Например, поставив задачу проведения исследования, в котором выбрано пять факторов при пяти уровнях, получим 3125 состояний. Очевидно, в таких условиях мы вынуждены отказаться от эксперимента. Естественно возникает вопрос, сколько и каких опытов нужно- включить в эксперимент, чтобы решать задачу.

За отказ от полного перебора состояний нужно платить.. Цена — это допущения, которые мы делаем относительно свойств неизвестной нам до опыта модели явления.

Модель — это вид функции параметра состояния У>={(Хи Х2..., ХК). Выбрать модель, значит, выбрать вид функции, за­писать ее уравнение. При многих факторах функция отклика (параметр состояния) представляется некоторой многомерной поверхностью. При экспериментальных задачах основные допу­щения относительно поверхности отклика,— непрерывность, гладкость и наличие естественного оптимума. Эти постулаты позволяют рассматривать изучаемую функцию в виде степен­ного ряда в окрестности любой точки факторного пространства:

А ■ ( и

У = + £ ^х + £ ^,Х{Х/ Б р, Х? + (15.2)

1 = 1 1=1 1=1

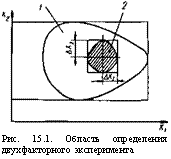
После выбора вида функции отклика следует установить границы области определения факторов. Для многофакторного эксперимента — это многомерная поверхность, в случае двух­факторного эксперимента область определения факторов пред­ставляется на плоскости (рис. 15.1).

В области определения необходимо найти локальную под­область для планирования. Процедура включает выбор основ­ного уровня и интервалов варьирования факторов. В боль­шинстве случаев после предварительного эксперимента коорди­наты наилучшей точки неизвестны, но уже есть сведения о под­области, где процесс идет хорошо. Тогда основной уровень вы­бирается в случайной точке этой подобласти. После того, как выбран основной уровень, переходим, к выбору интервалов варьирования. Интервалом варьирования ДХ называется неко­торое число, прибавление которого к основному уровню дает верхний уровень фактора, а вычитание — нижний (табл. 15.1).

Для упрощения записи уровней эксперимента и обработки данных масштабы по осям подобласти определения выбирают­ся так, чтобы верхний уровень соответствовал +1, а ниж­ний — 1.

При выборе интервалов варьирования факторов необходимо иметь в виду, что интервал варьирования не может быть мень­ше ошибки, с которой фиксируется фактор, иначе уровни ока­жутся неразличимыми; интервал не может быть настолько большим, чтобы уровни оказались за пределами определения.

При решении задачи оптимизации выбираем такую подоб­ласть, которая бы давала возможность шагового движения к оптимуму. В задачах интерполяции интервал варьирования охватывает всю описываемую область определения.

Полезно вести градацию интервалов варьирования факто­ров: узкий — до 10% области определения; средний — до

30 %; широкий — остальное.

Эксперимент, в котором реализуются все возможные сочета­ния уровней, называется полнофакторным (ПФЭ). Если на первом этапе исследования допустить возможность получения линейной модели, ПФЭ основывается на варьировании факто­ров на двух уровнях и называется полнофакторным эксперимен­том типа 2^.

Условия эксперимента в кодированной форме обычно дают в таблице, где строки соответствуют различным опытам, а столбцы — значениям факторов. Такие таблицы называются матрицами планирования эксперимента.

Введем следующие символы для табл. 15.2 1 — все факторы находятся на нижнем уровне; буквы латинского алфавита оз­начают, что в данной строке фактор соответствующего после­довательного столбца был на верхнем уровне.

Матрица планирования в символической форме может быть записана так: с, b, а, abc, (1), cb, са, ab. Такая форма записи особенно удобна для матриц многих факторов.

15.2.

Матрица планирования эксперимента 2к при k = 3

При большом количестве факторов возникает необходимость в формулировании приема построения матрицы планирования. Простейший прием состоит в том, что при добавлении нового фактора каждая комбинация уровней исходного плана встреча­ется дважды в сочетании с верхним и нижним уровнями нового фактора. Например, матрицу ПФЭ 24 в символической форме запишем так: cd, bd, ad, abed, d, cbd, cad, abd, c, b, a, abc, (1), cb, ca, ab. Полный факторный план обладает рядом важных свойств:

1. Симметричность относительного центра плана, выражаю

N

Щаяся условием £Х/, =0 (/ = 1, 2, k).

/=!

N 0

2. Нормировка, означающая, что =^ (у = 1, 2, ..., k).

I= I

3. Ортогональность, выражающаяся в том, что

%X-,tXul = 0 {j Фи, и = 1,2, k).

I=i

Это означает, что сумма почленных произведений любых двух векторных столбцов матрицы планирования равна нулю.

4. Рототабельность, т. е. точки в матрице планирования, подбираются так, что точность предсказания значений парамет­ра оптимизации одинакова на равных расстояниях от центра плана и не зависит от направления.

Ортогональность и симметричность плана позволяют полу­чить независимые друг от друга оценки коэффициентов регрес­сии:

N

= (/ = 0,1,2, к). (15.3)

Полные факторные планы дают возможность выявить влия­ние на функцию отклика не только каждого фактора, но и их взаимодействий. Для этого в матрицу планирования включают вектор-столбцы, содержащие фиктивный фактор Х0.

Матрица планирования эксперимента 23 с учетом взаимо­действий принимает вид табл. 15.3. Проанализировав матрицу планирования с учетом взаимодействия, увидим, что она обла­дает всеми свойствами матрицы ПФЭ. Это позволяет опреде­лить коэффициенты парных взаимодействий

В1т = —----- ^ ЦФт, }, т = 1,2, А). (15.4)

В условиях отсутствия эффектов взаимодействия коэффициенты регрессии Б, т будут очень малы, а функция отклика будет опи­сываться полиномом первой степени.

15.3. Матрица планирования эксперимен - 15.4. Матрица планирования