Теплонспользующие установки промышленных предприятий
Планы второго порядка
Двухуровневое планирование эксперимента с использованием матриц полнофакторного или дробнофакторного эксперимента позволяет при минимальном объеме эксперимента получить линейное уравнение регрессии (функции цели).
Методы планирования предполагают не только минимизацию объема эксперимента, но и отыскание оптимума (экстремума) функции цели. В таком случае уравнение регрессии должно аппроксимироваться полиномом второго порядка вида
У = Ро + Е № + Е Р//ВД + & (15.6)
1=1 , /—1 I—!
Для определения коэффициентов регрессии в уравнении (15.6) двухуровневые факторные эксперименты не пригодны, так как вектор-столбцы X* и Х в матрице планирования неразличимы. Поэтому для построения полинома второй степени необходимо варьирование факторов хотя бы на трех уровнях.
Двухуровневый эксперимент и линейную форму уравнения регрессии целесообразно использовать при отыскании подобласти экстремума (оптимума) функции цели. Переход к трехуровневому эксперименту и квадратичной форме уравнения регрессии следует осуществлять лишь после установления неадекватности линейной функции связи в подобласти экстремум а.
Согласно результатам исследований [58] наиболее рациональным является центральное композиционное планирование. Центральный композиционный план второго порядка получают достройкой некоторого количества точек к ядру линейного двухуровневого эксперимента. Если количество факторов /г менее пяти, за ядро плана принимают полнофакторный план эксперимента типа 2*, если же более пяти — то полуреплику от ПФЭ типа 2*. Такой выбор ядра обусловлен тем, что от ядра требуется раздельная оценка всех линейных эффектов и парных эффектов взаимодействий.
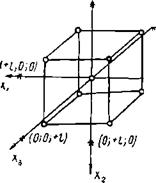
Для трех факторов схема центрального композиционного плана второго порядка изображена на рис. 15.2. Чтобы получить центральный композиционный план второго порядка для трех факторов, к полнофакторному эксперименту 23 добавляют шесть «звездных» точек с коэффициентами (/, 0, 0); (—I, 0, 0); (0, I, 0); (0, —/, 0); (0, 0, I); (0, 0, —/) и некоторое число п0 точек в центре плана. Центральный композиционный план для трех факторов можно представить матрицей вида (табл. 15.8).
|
15.8. Матрица центрального композиционного плана второго порядка для трех факторов
|
Ортогонализация матрицы планирования осуществляется преобразованием квадратичных членов X? новой переменной х[
N
Х = Х]-!-=^- = Х*-ХТ2: (15.7)
После замены Х на X,- сумма построчных произведений столбцов
2 Ха, Х'ц = 2 X?/ — АГХГ2 - 0. (15.8)
/=| =і
Так, в матрице центрального композиционного плана (см. таблицу 15.8) получим
Е Хо, Хи = 2 х0,{хЬ-хт2) = Е *?/- 15ХГ2 - 1=1 /=1 ,=|
Аналогично находим для переменных Хг и Хз. Ортогонализация соотношения
ЕХ?/Хи, Ф0 (I Ф и, I, и= 1, 2, к) (15.10)
/=!
Достигается выбором звездного плеча I (табл. 15.9).
|
Количество факторов |
Ядро Плана |
Количество дополнительных опытов |
«Звездное» плечо 1 |
|
2 |
2а |
5 |
1,000 |
|
3 |
2» |
7 |
1.215 |
|
4 |
24 |
9 |
1.414 |
|
5 |
25—1 |
11 |
1.547 |
|
15.9. Значения звездного плеча I, вычис - (діОі'І) ленные для различного числа факторов |
|
1-1,0,01 •* |
|
(0, -1,0) |
![]()
|
Рис. 15.2. Схема центрального композиционного плана второго порядка для трех факторов |
![]()
Если ортогональность выбрать за достаточный критерий оптимальности плана, то на число опытов в центре плана не накладывается никаких ограничений и /г = 1.
Подставляя I = 1,215 в уравнение (15.9) и в аналогичные для Хч. и Х3, получаем ортогональный центральный композиционный план второго порядка для трех факторов в виде матрицы (табл. 15.10).
Ортогональность, однако, не есть [58] достаточно сильный критерий оптимизации композиционного плана второго порядка. Наиболее эффективно использование центральных композиционных планов, отвечающих требованию ротатабельности, т. е. планов, позволяющих получать модель, способную предсказывать значения параметров оптимизации с одинаковой точностью независимо от направления на равных расстояниях от центра плана.
|
Содержание Плана |
ЛЬ Пп. |
*0 |
*1 |
*2 |
*3 |
Х, Х2 |
*2*3 |
*1*3 |
*1 - 0.73 |
А:|—о,7з |
Х£_о,73 |
У |
|
План 23 |
1 |
+ 1 |
+1 |
+ 1 |
+ 1 |
+ 1 |
+1 |
+1 |
+0.27 |
+0,27 |
4-0,27 |
Ух |
|
2 |
+ 1 |
-1 |
+ 1 |
+ 1 |
—1 |
+1 |
—1 |
+0.27 |
+0,27 |
+0,27 |
У 2 |
|
|
3 |
+ 1 |
— 1 |
+ 1 |
—1 |
—1 |
+1 |
+0,27 |
+0,27 |
+0.27 |
Уг |
||
|
4 |
+ 1 |
—1 |
— 1 |
+ 1 |
+ 1 |
—1 |
—1 |
+0,27 |
+0,27 |
+0,27 |
У* |
|
|
5 |
+ 1 |
+ 1 |
+ 1 |
—1 |
+ 1 |
—1 |
—1. |
+0,27 |
+0.27 |
+0,27 |
Уь |
|
|
6 |
+1 |
— 1 |
+ 1 |
— 1 |
— 1 |
—1 |
+1 |
+0,27 |
+0.27 |
+0,27 |
У6 |
|
|
7 |
+ 1 |
+ 1 |
—1 |
—1 |
+1 |
—1 |
+0,27 |
+0.27 |
+0,27 |
У 7 |
||
|
8 |
+ 1 |
—1 |
— 1 |
— 1 |
+ 1 |
+1 |
+1 |
+0,27 |
+0,27 |
+0,27 |
Уа |
|
|
«Звездные» |
9 |
+ 1. |
+ 1,215 |
0 |
0 |
0 |
0 |
0 |
+0,746 |
—0,73 |
—0,73 |
У9 |
|
Точки /= 1,215 |
10 |
+ 1 |
—1.215 |
0 |
0 |
0 |
0 |
0 |
+0,746 |
—0,73 |
—0.73 |
У10 |
|
11 |
+ 1 |
0 |
+ 1.215 |
0 |
0 |
0 |
0 |
—0,73 |
+0,746 |
—0.73 |
У XX |
|
|
12 |
+ 1 |
0 |
— 1.215 |
0 |
0 |
0 |
0 |
—0.73 |
+0,746 |
—0,73 |
У12 |
|
|
13 |
+ 1 |
0 |
0 |
+1,215 |
0 |
0 |
0 |
—0,73 |
—0.73 |
+0.746 |
Ух 3 |
|
|
14 |
+ 1 |
0 |
0 |
—1.215 |
0 |
0 |
0 |
—0,73 |
—0.73 |
+0,746 |
Уи |
|
|
Нулевая Точка |
15 |
+ 1 |
0 |
0 |
0 |
0 |
0 |
0 |
—0,73 |
—0,73 |
—0.73 |
Ухъ |
|
327 |
Ротатабельность достигается выбором значения «звездного»
Плеча для ядра, содержащего полный факторный эксперимент, из к
Соотношения 1 = 24 (15.11), а для ядра, содержащего дробную
К—р
Реплику,— из соотношения / = 2 4 (15.12). Для ротатабельного планирования второго порядка важное значение имеет выбор
Числа опытов в центре плана, так как оно определяет характер
Распределения получаемой информации о поверхности отклика (уравнении регрессии). Число опытов в центре плана выбирается так, чтобы обеспечить так называемое униформпланирование. Униформпланирование возможно, если
} _ й (пс + По) /.г 104
* - (Г+2К • (15ЛЗ)
Где п:, — количество опытов в центре плана; пс = N — п0; N — общее количество опытов; к — число факторов. Необходимо, чтобы X было немного меньше единицы (табл. 15.11).
|
15.11. Данные для построения матриц, центрального композиционного ротатабельного планирования второго порядка
|
Коэффициенты уравнения регрессии определяем, используя известные выкладки 158]:
2Цк +2) £ -2 ХС 2 £ Ху У;
|
(15.14) (15.15) (15.16) |
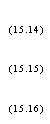 Ьо =
Ьо =
N
|
/=1 |
![]() £=1 1=1
£=1 1=1
&. = -£-£ ХцУп
Л /■= I
Г2 N
Ь, и = дД X, ХчХщУг,
Ьи = - ы - |с2 [(/г + 2) X - к £ Х2ЦУ, +
+ С* (1-Х) І £ ХїіУ і —2С £ У,, (15.17)
(=1 /=1 •=!
Где