Теплонасос

ЦИКЛ КАРНО

В 1824 г. Карно впервые использовал термодинамический цикл для описания процесса, и этот цикл остается фундаментальной основой для сравнения с ним и оценки эффективности тепловых насосов.

Тн

///////

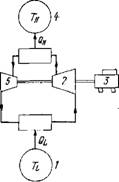
Рнс. 2.1. Термодинамическая схема теплового насоса н теплового двига­теля.

1 — тепловой иасос; 2 — тепловой двига­тель; Тн — высокая температура; Tl — низкая температура.

/ — источник тепла; 2 — компрессор; 3 — приводной двигатель; 4 — потребитель теп­ла; 5 — расширительная машина.

Тепловой насос можно рассматривать как обращенную тепло­вую машину. Тепловая машина получает тепло от высокотемпера­турного источника и сбрасывает его при низкой температуре, от­давая полезную работу. Тепловой насос требует затраты работы для получения тепла при низкой температуре и отдачи его при бо­лее высокой (рис. 2.1).

Можно легко показать, что если обе эти машины обратимы (т. е. термодинамические процессы не содержат потерь тепла или работы), то существует конечный предел эффективности каждой из них, и в обоих случаях это есть отношение Qh/W. Если бы это

Было не так, то можно было бы построить вечный двигатель, про­сто соединив одну машину с другой. Это отношение очень важно. В случае тепловой машины оно записывается в виде W/QH и на­зывается термическим КПД, а для теплового насоса оно остается в виде Qh/W и называется коэффициентом преобразования (КОП). Его следует отличать от аналогичного отношения Ql/W, приме­няемого в холодильной технике и называемого в дальнейшем КОПохл. Поскольку получается КОПОХл = КОП—1.

Цикл Карно на рис. 2.2 изображает рабочий процесс идеаль­ной тепловой машины, работающей в заданном интервале темпе­ратур. Стрелки показывают направление процесса для теплового насоса. Тепло изотермически подводится при температуре TL и изотермически отводится при температуре Тн• Сжатие и расши­рение производятся при постоянной энтропии, а работа подводит­ся от внешнего двигателя. Используя определение энтропии и за­коны термодинамики, можно показать, что коэффициент преобра­зования для цикла Карно имеет вид

КОП = TlI(Th—Tl) + 1 - THJ(TH-TL).

Никакой тепловой насос, созданный в пределах нашей Вселен­ной, не может иметь лучшей характеристики, и все практические циклы реализуют стремление максимально приблизиться к этому пределу.