Уравнение теплопроводности для анизотропного тела с источником энергии и переменными теплофизическими параметрами
Из обширного класса анизотропных тел рассмотрим такие, в которых тело имеет различные коэффициенты теплопроводности 2jc, Ху, Xz в трех взаимно перпендикулярных направлениях, принятых за оси координат х, у, z. Если принять это ограничение, то останется справедливой запись закона Фурье в форме (1.2). Предположим, что в объеме AV= AxAyAz могут находиться источники тепла, удельная мощность которых в момент
л
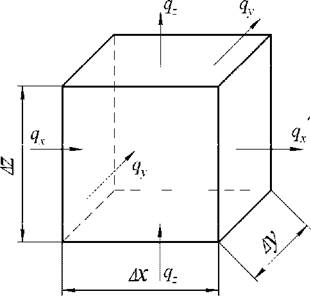
времени г равна W(x, у, z, г), Вт/м (рис.2.1).
Рассмотрим изменение теплового состояния объема AV за промежуток времени dx. При этом будем базироваться на двух законах: законе сохранение энергии и законе Фурье.
Количество тепла, поступающего в объем слева через поверхность AyAz за время dr, обозначим dQx, а количество тепла, выходящее из объема AV через правую поверхность AyAz, обозначим dQ'x. Аналогично введем обозначения dQy, dQ’y, dQz, dQ’z, Пусть за время dr температура t( х, у, z, т ) объема А V повысилась на dt градусов, тогда количество тепла, поглощенное объемом, равно cpAVdt; действие источников тепла вызовет дополнительное поступление энергии, равное WA Vdr.
На основании закона сохранения энергии:
|
|
|
|
dQx + dQy + dQ, + WAVdr = dQ'x+dQ'y +dQ'z+cpA Vdt, (2.1)
|
|
|
Рис. 2.1. К выводу дифференциального уравнения теплопроводности На основании закона Фурье имеем |
|
dt_ удху |
|
dr, |
|
(2.2) |
|
dQ 'x —q AyAzd т = ~ЛХ AyAzi — ) dr, SxJx+Ax |
|
dQx = qxAyAzdr = — AxAyAz |
где qx, q'x - удельные тепловые потоки в направлении оси х. Аналогично записываем выражения для направлений у иг:
|
dr, |
|
ду |
|
J |
|
dQ = q AxAzdr = - Л AxAz |
|
(2.3) |
|
dr, |
dQ'y —q'yAxAzdv = ~Л AxAz
|
dQ_ = q_AxAydr = — AzAxAy |
|
ґділ |
|
dz |
|
dQ'z =q': AxAyd г = ~AzAxAy |
|
dr; |
|
dt V ^ / z+Az |
|
Jr. |
Подставим (2.2) и (2.3) в равенство (2.1):
|
rdt_^ убХу (ск_л |
|
■ AxAyAz • AxAyAz |
|
dr — AyAxAz |
|
dr + WAxAyAzd т |
|
(2.4) |
|
№ |
|
d г AyAxAz |
|
/ XT Дх |
|
dr ~ ДДхЛуІ — I dr + cp AxAyAz dt. dz)7+iz |
|
— j dr-AzAxAy дУ У ^ |
|
v |
Заметим, что t есть функция х, у, z, т, а следовательно, произведение
есть функция х, у, z, т; здесь г = х, у, z.
Обозначим последнее произведение через Ф[, т. е.
|
*) |
|
Ф |
|
(2.5) |
|
НГ |
|
Л іУАі |
Используя обозначение (2.5), перепишем равенство (2.4):
|
(2.6) |
Дх Ау Az дт
Переходя в (2.6) к пределу при Аі—*0 и используя определение производной
Ф,+А,“Ф, дФ,
lim
|
ді |
ді-fO Зі
|
w dt ■Н - + Ж = С/7---------------------- & Эг |
бФ, ЙФ, сФ
Получим -
дх ду
на основании определения (2.5)
|
& dz |
|
dt |
|
ы_ дт |
|
л. |
|
д. |
|
+ W = ср |
|
(2.7) |
|
+■ |
|
+ ■ |
|
дх |
|
ФЧ дУу |
|
dz |
|
йх |
Это и есть дифференциальное уравнение теплопроводности для рассматриваемого класса анизотропных тел с источниками тепла и теплофизическими параметрами, зависящими от температуры.
Рассмотрим класс анизотропных тел в цилиндрической системе координат. Пусть коэффициенты теплопроводности в направлениях х и z равны Ах и А-. Тело ограничено плоскостями, перпендикулярными оси z.
Для таких тел уравнение теплопроводности с учётом осевой симметрии имеет вид
|
dt |
|
dt & |
|
dt а7 |
|
і а |
|
, ^хХ хдхУ дх |
|
Я |
|
+ W = ср |
|
(2.8) |
|
dz |
Замечание. Как уже отмечалось, в общем случае для анизотропной среды направление вектора теплового потока в какой-либо точке, вообще говоря, не совпадает с направлением нормали к изотерме, проходящей через эту точку, а закон Фурье записывается в ином виде:
, dt. dt. dt -qx _ +Л - 2 +A, _ :
dx dy dz
_ . dt, dt dt w
7У — ^21 _ + ^22 - + ^23 - ’
dx ay dz _ . dt dt dt щ
4z ~ ^11 - + ^32 - + ^ЗЪ - ’
ax dy dz
где Лп -коэффициенты теплопроводности (компоненты тензора второго
ранга). Общая теория переноса тепла через анизотропные среды изложена в [10].