Тепловое сопротивление плоской, цилиндрической и сферической стенок
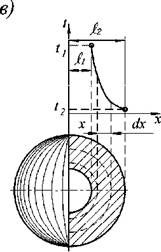
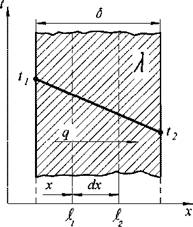
На рис. 1.7 изображены однородные стенки различной конфигурации, поверхности которых X=h И Х=12 являются изотермическими с температурами t} и t2 , а торцы плоской и цилиндрической стенок являются адиабатическими; внутренние источники тепла в стенке отсутствуют; коэффициент теплопроводности материала - X. Найдем выражение для стационарного теплового потока Ф через эти стенки.
Воспользуемся зависимостями (1.14) и (1.15), связывающими разность температур (ti - ti) с тепловым потоком Ф, а значение теплового коэффициента F найдем для каждого конкретного случая с помощью выражения (1.19).
Элемент длины dn пути теплового потока для плоской (п), цилиндрической (ц) и шаровой (ш) стенок равен dn = dx, а аналитические выражения А(х) изотермических поверхностей имеют вид Ап =Lj L2 , Ац =2жхЬц, Аш=4жх2, где L] и L2-длина и ширина плоской стенки; L4— длина цилиндрической стенки.
Поскольку по условиям задачи между изотермическими поверхностями отсутствуют источники и стоки энергии, коэффициент F имеет смысл теплового сопротивления, которое для плоской, цилиндрической и шаровой стенок обозначим через R„, RH, Rm.
Учитывая неизменность потока тепла Ф(х)=соп$і и подставляя значения dn и А(х) в выражение (1.19), получим
|
JLL^Lj |
ЛЬХЬ2 ЛАп |
|
дх |
1 г dx |
|
Л2 лхЬа |
ІяЛЬ • х ц ^ |
|
■ дх |
і 1 |
|
Л4лх2 |
4пЛ Xі 1 |
|
Rm=) |
|
vO>y |
|
а) б) (1.22) в) |
где 8 = І2~ h~ толщина плоской стенки.
|
а) |
|
б) |
|
|
|
{, |
|
|
|
|
|
Si |
|
а- |
|
/4-' |
|
t'4.J |
|
А |
|
|
Рис. 1.7. К расчёту теплового сопротивления стенок различной
конфигурации