Температурное поле стержня с источником тепла
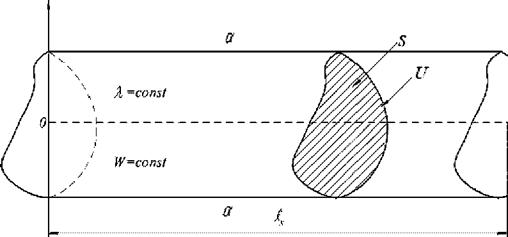
Пусть стержень имеет постоянное поперечное сечение S и периметр U. Теплообмен стержня со средой описывается законом Ньютона, средний коэффициент теплообмена равен а. Материал стержня имеет постоянный коэффициент теплопроводности А. На одном торце стержня * = 0 задан тепловой поток Р, а на другом торце х = 1х теплообмен происходит по закону Ньютона с коэффициентом теплообмена аТ. Температура окружающей среды всюду постоянна и равна tc.
Полагая в (2.99) W* = const = w и принимая Ь2 по формуле (2.103), получим дифференциальное уравнение, описывающее температурное поле стержня (рис. 2.10):
12л ^ П I 2 aU п, ч
-Ъ9 + — = 0, b =-^г, 9 = t(x)-te
|
dx |
|
Л |
IS
Условия на границах имеют вид
|
йЭ_ dx |
|
■Л |
■S = Р
с=0
dx Я
|
Рис. 2.10. Стержень произвольного сечения Общий интеграл равен |
х
W
|
(2.115) |
3(х) = Cychbx + C2shbx + —j.
ЛЬ
Из граничных условий находим
С2=-— С, =-^—А---------- с^—
Я5Ь ЯЗЬ Я2Ь2(Ь$}гЫх + —chblx)
Я
Окончательное решение примет вид
р W ITchbx
$ = ——(Achbx-shbx) + — (l -------------- ). (2.116)
Ш ЛЬ shbl + — chbl
х ЛЬ
Рассмотрим частные случаи.
а) Теплообмен с торца х = 1х отсутствует (адиабатический торец). Это означает что ат = О и (2.116) примет вид
<9 = —— (Achbx ~ shbx) + -^-г-, А - cthbl
XSb ЛЬ2
или
Р chb(l - я) W
~ XSb shbl. +Jb2’ (2.117)
б) То же, что и (а), но отсутствуют внутренние источники энергии W = 0.
. Р chb(lx - х)
~ IbS shblx ' (2.118)
Обозначим температуру торца х = 0 в этом случае через &0 и найдём связь между i9(l и Р
9 = — cthbl х Р = 30ASbthblx. (2.119)
XSb
Условие (2.119) позволяет записать формулу (2.118) для случая, когда задана на границе х = 0 не мощность Р , а перегрев 30; действительно,
|
,9 = 9, |
chb(lx - х)
0---- Г71—•--------------------------------------- (2.120)
chblx
Из сопоставления (2.116) и (2.117) следует, что расчётная формула существенно упрощается, когда соблюдено условие ат = 0. Покажем, как
для аг ф 0 можно решение (2.116) привести к приближенной формуле, имеющей структуру (2.117), из условия сохранения общего теплового баланса. Для того, чтобы в (2.117) учесть теплоотдачу с торца стержня (снять условие ат = 0 ), следует условно увеличить площадь боковой поверхности стержня путем увеличения длины стержня. Тогда условная длина стержня станет равной 1'х . Эти параметры связаны очевидными
соотношениями:
(lx-lx)-U а = Sa7
Откуда
и a v '
Подставив в уравнение (2.117) вместо 1Х условную длину /’ , учтём теплообмен торца с окружающей средой.
в) Полуограниченный стержень 1Х= да. Выражение для А примет вид
TOC o "1-5" h z Р W
9 =--------------------------------------------------------- (2.122)
XSb п1 у - )
Здесь использованы известные зависимости
chx - ^(ех + е~х); shx - “ е *)-
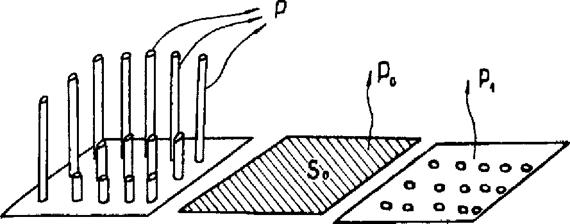
Пример 1. Для увеличения рассеяния тепловой энергии с поверхности S0 торца функционального микроминиатюрного элемента выведено п медных (А, = 400 Вт/м-К) жил диаметром 2Д = 10~3 м, длиной / = 10 мм (рис. 2.11). Пусть 50=1 см, коэффициент теплообмена между поверхностью и средой при отсутствии жил а0=Ю Вт/м К, коэффициент теплообмена
одной жилы с окружающей средой а = 20 Вт/м - К.
Найти, во сколько раз увеличится отток тепла с поверхности при наличии жил. При решении задач считать, что наличие жил не изменяет значений коэффициентов теплообмена а и а0.
Решение. Обозначим мощность, рассеиваемую с поверхности жил, - Р; мощность, рассеиваемую оставшейся поверхностью (при наличии жил), ~Р{.
Р + Р
Требуется вычислить отношение L.
^0
|
Рис. 2.11. Увеличение интенсивности теплообмена с помощью медных жил |
Найдём
Здесь через 90 обозначен перегрев над средой поверхности 50 . Если пренебречь количеством тепла, рассеиваемым с открытого торца жилы в среду, то на основании (2.119)
Р = п 90ASbthbl
Значение Рх найдем из очевидного равенства
Рх = айЭ0(80-плИ2)'
Итак,
nR2
nXbSthbl+ a. nS(i(l-n )
TOC o "1-5" h z Р + Р{ S0 nXbS,,, , 7iR2
1 - 0 - - thbl + l-n
P0 ао*^о S0
6i = ot/ = 2a= 2.20 _1_
XS XR 400 0,5 10 m м
Ы = 0,14; thbl * 0,14;
P + P L = 1 + «- 0,62.
P0
Если n = 10, то рассеяние увеличивается в 7 раз.
Замечание. Вывод (2.119) сделан в предположении, что основание жилы
имеет температуру 90, а коэффициент теплоотдачи на поверхности жилы а остается неизменным. Однако с увеличением количества жил, если не принимать специальных мер, интенсивность теплообмена на их боковых поверхностях будет снижаться и последняя формула дает завышенный результат. Дальнейшее увеличение количества жил приведет к противоположному эффекту.
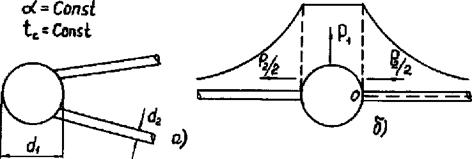
Примет? 2. Полупроводниковое термосопротивление типа бусинки имеет следующие параметры (рис. 2.12): диаметр бусинки d{= 1 мм, диаметр медных проводников d2 = ОД мм, их коэффициент теплопроводности Я2 = 400 Вт/мК, длина проводников во многом превышает их диаметр, т. е. можно считать 12 = со. Бусинка находится в воздухе, коэффициент теплообмена проводов и бусинки со средой а = 40 Вт/м К.
|
|
|
Рис. 2.12. Полупроводниковое сопротивление бусинкового типа |
|
X |
Необходимо найти величину измерительного тока, при котором погрешность измерения температуры tc воздуха из-за перегрева
термосопротивления не превысит 0,1% ; tc = 40 °С. Электрическое сопротивление R =2500 Ом при tc= 40 °С.
Решение. Обозначим допустимый измерительный ток через 1$ , он связан с рассеиваемой допустимой мощностью Р$ зависимостью
|
|
где R - электрическое сопротивление термистора. Погрешность измерения б за счёт перегрева термосопротивления равна
|
(а) |
<у = ^-А = —= 0,001 = io_3,5d =io_3f<
t „
Это значение 0 будем считать допустимым и обозначать 9д. Установим
связь между 9д и Рд. Для этого представим термистор в виде бусинки с равномерным полем температур и двумя стержнями (рис. 2.12 б). В стержни отводится поток Р2 , а со свободной поверхности ПТС рассеивается поток Р1. Полная мощность Рд равна
Рд=Р,+Р2 (б)
Найдём Р{:
Р{ = a&dSx = а9д ^ • 2) = 9д ■ 1,25 - КГ4 Вт
Полагая, что Р2 /2-поток, входящий в один торец бесконечного стержня с температурой основания 9д, по формуле (2.119) найдём
Поток, входящий в оба проводника, равен
Р2 =29A2b2S2 =9д -2-4-102J 440 *Л0 =4-10~4^ Вт.
й й V 400 10“ 4
Итак,
Рд = (1,25 + 4) • 1(Г4 Эй = 5,25 ■ 10~4 &д Вт.
Из (а) и (б) находим
Рд =5,25-КГ4 -1(Г3 ■40 = 2,Ы0""5 Вт.
Из (а) также следует, что перегрев термосопротивления при этой мощности будет равен
<9 = 10~3fc = 0,04 К,
т. е. электрическое сопротивление следует брать при температуре t = 40,04 °С; будем считать его мало отличающимся от заданного R =2500 Ом при t = 40 °С. Тогда
|
|
|
= 92 мкА |