Составные стенки. Применение законов Кирхгофа
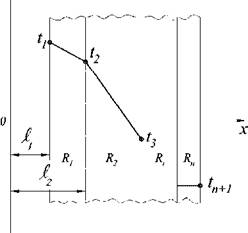
Рассмотрим теперь последовательно составленную плоскую стенку, состоящую из п разнородных, ориентированных перпендикулярно потоку тепла слоев, ТОЛЩИНЫ И коэффициенты теплопроводности которых - £>г и 2, .Температура наружных поверхностей стенок равны t} и tn+1 (см. рис. 1.8 а).
Изотермическими поверхностями в этом случае являются плоскости, параллельные поверхности стенок. Между изотермическими поверхностями отсутствуют стоки и источники энергии и тепловой поток, не изменяясь, проходит через все стенки. Следовательно, каждой стенке
|
б) |
а)
|
|
R= I R;
|
ln I I |
t,* ПИ С
R, R2
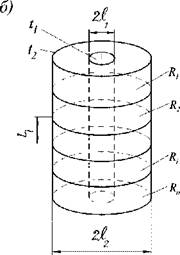
Рис. 1.8. Последовательное соединение стенок
можно приписать тепловое сопротивление Ri, все тепловые сопротивления, как это видно согласно рис. 1.8 б, соединены последовательно, т. е. суммарное тепловое сопротивление:
(1.23)
На основании (1.14) между температурами ti и tn+1 и тепловым потоком Ф справедлива зависимость
|
(1.24) |
PR = E^L_
s ti4
Проведём аналогичные рассуждения для тепловых сопротивлений последовательно составленных цилиндрической и сферической неоднородных стенок, состоящих из п неоднородных слоёв, расположенных перпендикулярно потоку тепла:
|
(1.25) (1.26) |
|
і г |
|
1 _ 1 X~~L |
|
4 тгІҐА, |
|
z=l /iji li *7+1 J |
где It - радиус z'-го цилиндрического или сферического слоя; Ьц - длина цилиндра.
Найдём выражение для теплового сопротивления параллельносоставной стенки, образованной системой плоских стенок, расположенных параллельно потоку тепла (рис. 1.9 а).
|
в) |
|
Рис. 1.9. Параллельное соединение стенок |
|
R; |
а)
|
h p |
|
|
ІШІ |
|
|
A |
6 |
Ограничивающие поверхности с температурами ti и І2 являются равноотстоящими плоскостями, ориентированными перпендикулярно тепловому потоку. Для определения теплового сопротивления параллельно-составной стенки введем допущение, что разнородные стенки отделены одна от другой бесконечно тонкими адиабатическими (не проводящими тепла) прослойками. Тогда температурное поле в каждой стенке становится одномерным, и ее тепловое сопротивление может быть рассчитано по формуле (1.22 а). Тепловые сопротивления отдельных стенок соединены параллельно (см. рис. 1.9 в), поэтому их общее тепловое сопротивление потоку тепла равно
|
1 R |
|
R |
|
(1.27) |
|
У, ^ і а і г-1 |
|
1=1 |
Принятое допущение о наличии адиабатических прослоек позволило существенно упростить вывод выражения для теплового сопротивления параллельно-составной плоской стенки. Нетрудно получить выражение и для теплового сопротивления параллельно-составной цилиндрической стенки (рис. 1.9 б). Полагая, что разнородные стенки отделены одна от другой адиабатическими прослойками, из формулы (1.22 б) для Кц и схемы соединений сопротивлений (рис. 1.9 в) получим
In —
|
(1.28) |
R = ^JL^' R=^J:—R = lA
Z - 2nXik h V,
і=і Ri i=i
где Lr длина z-ro участка цилиндрической стенки.
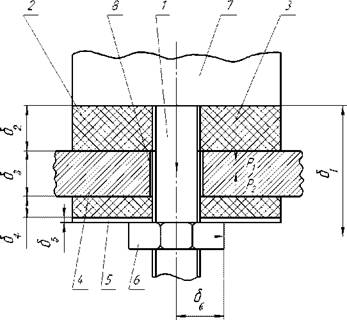
Сложное соединение стенок. При расчете тепловых сопротивлений различных технических устройств чаще встречаются случаи сложного соединения, в которых тела в системе соединены как последовательно, так и параллельно. Примером такого соединения может служить крепление некоторых деталей к шасси с помощью болта (рис. 1.10 а). В этом случае корпус детали электрически изолирован от шасси шайбами 2 и 4 из электроизоляционных материалов, которые одновременно являются и теплоизоляцией.
|
а) |
|
|
|
Рис. 1.10. Пример сложного соединения стенок |
|
R, |
|
Я, |
|
Я* |
|
R, |
|
б) |
Болт 2 отделен от шасси воздушной прослойкой 8, поэтому теплообмен через прослойку между болтом и шасси практически отсутствует. Тепло от детали к шасси поступает двумя потоками Ф/и Ф2 Поток Фj идет непосредственно через изоляцию 2, поток Ф2 - более сложный путем: от детали 7 через болт 1, гайку 6, шайбу 5 и слой изоляции 4. На рис. 1.10,а пути тепловых потоков обозначены стрелками. В данном случае тепловые потоки Ф/ и Ф2 движутся параллельно, преодолевая тепловое сопротивление R2 участка 2 и тепловое сопротивление нескольких последовательно соединенных элементов. На рис. 1.10,6 представлена общая схема соединения тепловых сопротивлений для рассматриваемого случая. Если предположить, что тепловой поток, проходящий через отдельные участки системы, не рассеивается, то результирующее тепловое сопротивление R крепёжного соединения найдем на основании закона Кирхгофа, а именно:
Параметры дА и А6 в данном примере довольно условны, приближенные методы их определения устанавливаются в каждом конкретном случае.