Обобщенное решение уравнения Бесселя
Постановка задач теплопроводности в цилиндрической системе координат часто приводит к уравнению Бесселя. В частности, уравнение теплопроводности (2.109) для диска является уравнением Бесселя. Уравнение этого типа путём преобразований обычно приводится к канонической форме, для которой известны решения. Иногда бывает довольно сложно найти такую замену независимой переменной, которая позволила бы преобразовать (если это вообще возможно) заданное дифференциальное уравнение в обычное уравнение Бесселя или же такое уравнение, общее решение которого содержало бы линейные комбинации функции Бесселя. Однако простое сравнение заданного дифференциального уравнения с приводимым ниже обобщённым уравнением Бесселя позволяет просто ответить на вопросы: сводится ли данное дифференциальное уравнение к уравнению типа Бесселя и каково решение этого уравнения. Одна из форм обобщенного уравнения Бесселя имеет вид [7]:
х2^ + [(1 -2А)-х - 1Bx2]^ + [C2D2x2c +В2х2 - В( 1 -2А)х + А2 -С2п2]у -0, (2.123)
dx dx
где п определяет порядок уравнения Бесселя. Обобщённое решение имеет вид [7]:
|
(2.124) |
y = xAe*[ClJ„(Dxc) + C2Y„(Dxc)l
где Сі и Сг - постоянные интегрирования; Jп и Yn - функции Бесселя
первого и второго рода порядка п.
Рассмотрим простейшую форму уравнения Бесселя вида
|
|
Его решение имеет вид
|
(2.125) |
У ~ CXJо (т) + C2Y0 (х),
где J0(x) и У0(х) - функции Бесселя вещественного аргумента нулевого порядка, вторую из них иногда называют функцией Неймана.
Напомним некоторые свойства функций Бесселя.
Первые производные функций нулевого порядка JQ(x) и Г0(х)
являются функциями Бесселя первого порядка
|
J, |
|||||
|
г-7/ д \ |
|||||
|
/Л /1 |
V л |
А, |
|||
|
1 1 / 1 1 1 |
V Л А х |
1 I / |
/ // |
^ ч / . |
* |
|
! |
Л * / Л к V |
// 4Jи у |
/ / |
||
|
'1 1 о 1 ! і і |
|||||
|
I! і і |
|||||
|
і1 |
|||||
|
| 1 ! і |
і |
|
./'„(*) = -/,(*), Y'0(x) = - Yl(x) |
|
О -0,2 ] -0,4 |
|
(2.126) |
|
0,1 |
|
X |
5 10
Рис. 2.13. Функции Бесселя и Неймана вещественного аргумента нулевого
и первого порядков
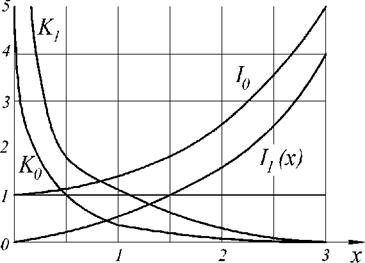
На рис. 2.14 представлен вид функций Бесселя /0(х),АГ0(х) нулевого порядка и первого порядка АГ,(х) и /,(х) . Функция Kv(z) называется функцией Макдональда.
Функции Кй(х) и ATj(x) при малых значениях аргумента могут быть представлены в виде
|
(2.127) |
АГ0(х)«1п(-)-0,577
X
АГ, (х) « х~' х < 0,5
|
Рис. 2.14. Функция Бесселя мнимого аргумента К0(х), К](х), Іо(х), 11 (х) |