Нагревание или охлаждение тела в среде с постоянной температурой
Пусть Р=0 , и тело помещено в среду с постоянной температурой tc = const. Тогда F0=F = tc = const, и зависимость (2.70) примет вид
© = —^ = £гт»(г~г»), (2.71)
*0 ~ К
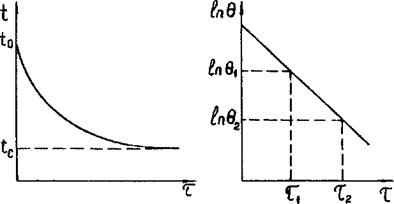
Из последнего выражения следует, что разность температур тела и среды изменяется по закону экспоненты (рис. 2.5 а).
Прологарифмируем формулу (2.71):
In 0 = ~т0 (г ™ г0) = ~м0т + пг0т0 = ~т0т + const. (2.72)
|
|
|
Рис. 2.5. Охлаждение или нагревание тела в среде с постоянной температурой |
а) б)
На рис. 2.5, б дано графическое представление этой зависимости в полулогарифмических координатах. Из рис. 2.5, б и формулы (2.72) следует, что
in 0. - In 0, 1п(т - tA - ln(f 2 -1 )
тn =---- !------------------- 2- = ^^^ (2.73)
Тг Г, т2 Г[
Последнее выражение позволяет определить параметр тй, который в
дальнейшем будем называть темпом охлаждения (нагревания) тела, опытным путём.
Пусть из опыта получена зависимость (t~te) = f(r); построив её в полулогарифмических координатах 1п(г-*с) = fx(r) и выбрав два каких-либо момента времени и г2, находим по формуле (2.73) величину т0. Полезно аналитическое представление темпа охлаждения тела т0 в иной форме: дифференцируя (2.72), получим
d п0
~т0 или
dr
d® d(t~tc) (2<74)
®dr (t-tAdr
Рассмотрим теперь простое нагревание тела в среде с температурой tc >tQ.
Вычтем из правой и левой частей уравнения (2.71) по единице. После преобразований получим
(2.75)
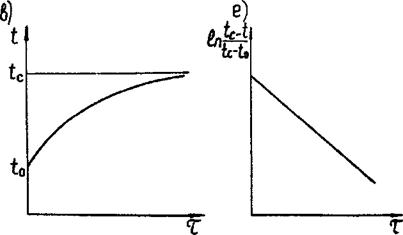
Графическая зависимость представлена на рис. 2.5.
Сделаем следующие тождественные преобразования с выражением
(2.75):
t-t0 =t-t0 + tc - tc
tc-t=(tc~tQ)e^4).
Представим, наконец, это выражение в виде
t ~t
In = - т0т + const
tc ~ t0
и изобразим последнюю зависимость графически (рис. 2.5). Если имеется экспериментальная зависимость t = /(г) по нагреванию тела в среде с температурой tc >t0, то можно определить темп нагревания тела по аналогии с темпом охлаждения тела. В этом случае результаты опытов следует обрабатывать в форме
1п(^ ~t2)
то=—— _ —(2.76)
Т2 г,
При простом нагревании или охлаждении тела с равномерным полем температур темпы нагревания и охлаждения, как это видно из всех предыдущих выводов, равны между собой.