Тепломассообмен

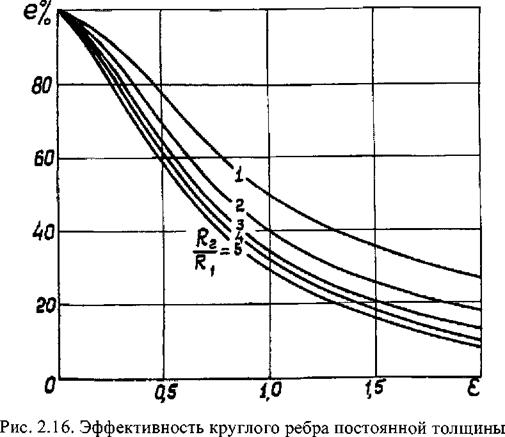
Эффективность круглого ребра постоянной толщины

Рассмотрим дальше частный случай W = О, т. е. круглый диск без источников тепла, и найдём эффективность ребра е: отношение полного количества тепла, рассеянного ребром, к тому количеству, которое рассеивалось бы в случае, если бы вся поверхность ребра находилась при температуре to основания ребра (или X = оо), т. е.

P0=(a'z+aMR22-R?)(t0-t сзф).

Эффективность ребра является важной технической характеристикой при выборе параметров ребра.

Обозначим

Іі(гЖі(п)-^і(7)Іі(7і) тогда эффективность ребра

В:

2Шу, В _ 2 В

+ (1 + R2/Rl)s Я,

(2.131)

s = (S2-R,)Ja'' + an'

ад

Зависимость е = е(є,—) приведена на рис. 2.16. Если Д2-»со, то

Ri

A (bR2) —> оо и решение (2.129) принимает вид

Р К0(Ьх)

3 =------------------------------------------------------ (7 1321

2nR{XSb Kx{bRx)

Покажем в заключение, что решение (2.129) можно обобщить, учтя приближенно отвод тепла с торца х = К2. Пусть толщина ребра значительно меньше (R2 - J?,), тогда некоторым увеличением радиуса R2 до /г20 можно учесть дополнительный отвод тепла с торца в среду с температурой гсэф.

Величину R10 найдём из равенства

2яК10 = 2кЩ + 2 kR2S,

Откуда