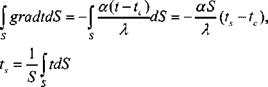Тепломассообмен

Дифференциальное уравнение процесса

Рассмотрим тело произвольной конфигурации, которое имеет мощность источника W(r). В начальный момент времени т = 0 тело имеет температуру t0

*L='o. (2.61)

и вносится в среду, температура tc(т) которой изменяется во времени; теплообмен тела со средой подчиняется закону Ньютона (2.24). Задача состоит в определении температуры тела в любой момент времени. Температурное поле такого тела описывается дифференциальным уравнением (2.10)

vh+W=cpBt_'

X X дт

граничным условием (2.24) и начальным условием (2.61).

Приведём эту систему уравнений к иному виду, применив ко всем членам системы уравнений следующую операцию:

Рассмотрим сначала (2.10):

J V~rdV = J gradtdS

s

и преобразуем первый член (2.62), при этом будет использовано граничное условие (2.24):

Тогда

По определению

где Р - полная мощность источников тепла в теле; t - средняя объёмная

температура тела.

В этих преобразованиях предположено, что коэффициенты а, Л, с не зависят от температуры. Используем полученные результаты и перепишем (2.62) в виде

dtv, . Р(т)

— + m„ts = m0tc (т) + ——, dt С

С = cpV, m

Если предположить, что поле температур в теле равномерное, то tv=ts= t, и уравнение (2.63) примет вид

Система уравнений (2.61) и (2.64) полностью описывает температуру тела с равномерным полем температур.