Анализ ошибки измерения температуры
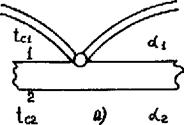
Ошибки за счёт оттока тепла по проводам термопары могут быть полностью устранены только в случае равенства температур пластины и окружающей среды. Такой предельный случай встречается редко, поэтому рассмотрим реальный процесс измерения температуры термопарой (рис. 2.17 а).
Пусть поверхности 1 и 2 тонкой пластины омываются средами с температурами tcl и tc2 с коэффициентами теплообмена а, и а2 ; термопара прикреплена к поверхности 1 пластины и находится в среде 1.
Рассмотрим случай, когда > *С2 , тогда термопара становится источником, а разность между тепловым потоком Pi, подводимым к спаю,
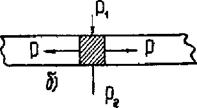
и потоком Р2, рассеянным на лицевой стороне круглого источника, равна р^.рх~р2 мощности источника. Выразим Рх и Р2 через термические проводимости (рис. 2.17 б)
|
|
|
|
Рис. 2.17. К оценке погрешностей измерения температуры с помощью
термопары
Рх — СГ1Г (fc] — t{ ) , Р2 — <72 (tx — tc2 ) ,
где ахт- тепловая проводимость термопары между спаем и средой 1, сг2- тепловая проводимость между лицевой поверхностью 2 источника и средою 2. Тогда
Р = (crXTtcX + <j2tc2) - {<гхт + сг2Х (2.133)
Для вычисления температуры tx можно воспользоваться соотношением
(2.132)
f =t і р K^bR^
1 "ф 2rtBLxSM> Kx(bRx) ’
* _ «7,1 + U2 _ «1 + «2
ax + a2 xd
Подставим в последнее выражение значение Р:
р _ («17^с1 «2^с2 ) ~ («1Г «2 )^1 ^0 (^^1 )
1 сэф_ 2жЯхШ Kx(bRx)
Заметим, что tx - температура, зарегистрированная термопарой; tc. i<p -
характеризует или температуру пластины в точке х = оо, или температуру пластины при отсутствии термопары. Разность (г, - ісзф) представляет собой
абсолютную ошибку измерения температуры контактным способом
с помощью термопары. Обычно а]Г »<т2, поэтому можно положить а2 =0, и последняя формула примет вид
Г ~Кзф _ 1
О ~КэФ і + 2л-j^bR, (2.134)
<т1Г K0(bR{)
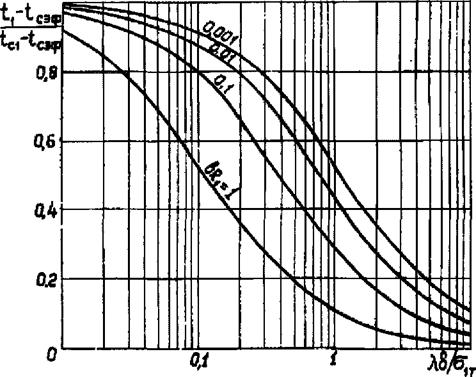
На рис. 2.18 приведена зависимость
т—-=/(—№,), « = ((.,-к»т—м, х
VI с эф &Т ^1Т
где по оси абсцисс отложено отношение проводимости диска к проводимости термопары.
|
Рис. 2.18. График зависимости —— |
Г-1 — Г эф &1Т
Для определения <т1Г можно воспользоваться результатами решения задачи о стержне (2.119). Обозначим теплопроводность термопары Д, площадь её поперечного сечения - ST, параметр Ь для термопары - через Ьт, её длину - /г; учтём также, что термопара состоит из двух электродов 1 и 2, поэтому (2.119) запишем в виде
Ру — — (^cl ^1 ^){^AjybjySjythbjyljy T A-^2Ь^2Sy^tbbj^^^T1 ^r
Далее примем во внимание, что длина термоэлектродов значительна, так что thbTlT ~ 1. Тогда
(J|jr ^Т^Т1^Т ^ ^7'2^7'2^'
2 _ аті^ті і2 _ ССтг^ті Т л ҐУ 5 Т2
Г25
*nSn 2ST2
Окончательно получим
(J j jr ” jf/'j4 I 2^^у2>^22 *
Если провода термопары изолированы, то изоляцию можно представить по формуле для плоской стенки. В последнюю формулу в этом случае следует вместо ап подставить а,, найденное из формулы
1 1 Лг
+ ^ (/=1,2),
ОС O'. J2 /(
где Лг и А - толщина и теплопроводность изоляции электрода. Вычисления по формуле (2.134) можно упростить, если вместо K^bRy) и K0(bRy) подставить асимптотические выражения, справедливые для малых x = bR{:
Ку(х) - х~ (х < 0,05); К0(х) = Inf-1 - 0,577, (х < 0,05).
х)