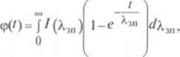Теория и практика экструзии полимеров
ЗАВИСИМОСТЬ ВЯЗКОСТИ ОТ ТЕМПЕРАТУРЫ
|
Хорошо известно, что температура оказывает значительное влияние на реологические свойства материалов. Это утверждение особенно справедливо дтя высоко полимеров. В данном разделе рассматривается влияние температуры на вязкость. Предметом |
|
Для частного случая, при п = I, уравнение (1.49) приводит к результату, полученному для ньютоновского течения в примере 1.1. |
|
(1.49) |
п. к тшцсго обсужления являются инженерные методы исследования юмпературной зависимости вязкости неньютоновских жид - ■ опей; эта задача особенно важна для процессов переработки ночи мерой.
< )бычно вязкость жидкостей уменьшается, а вязкость газов увеличивается с возрастанием температуры, что указывает на заметши различие в механизмах течения жидкостей и газов. При низ-
• их плотностях вязкость газа может быть определена теорегичес - - им анализом обмена количеством движения между смежными
• ноями молекул, движущихся с различными скоростями. В жид - MiM состоянии проблема является значительно более сложной: в ной области не было сделано попыток дать молекулярную интср - ирпаиию течения полимеров.
Поведение ньютоновских жидкостей при течении зависит от ишетвенной характеристики — вязкости, которая является толь - ю функцией температуры. Наиболее часто используемое выражение для зависимости вязкости от температуры — уравнение Аррениуса [1, 5):
= AeE! RT, (150)
| I К газовая постоянная; Е - энергия активации течения; А - коэффициент. 1Н1КШПИЙ от природы жидкости.
Уравнение (1.50) можно исследовать, используя графическую миисимость Igp от (1 /Т). Для большинства жидкостей в темпе - р. мурной области выше 40 °С можно получить довольно четкую прямолинейную зависимость. Вне этой области график обычно и и ибается, указывая на то, что изменения величин А и Е с ini' пением температуры становятся существенными. Иногда для 10ЧПСНИЯ данных зависимости вязкости от температуры полезно применить другое уравнение:
i = ae~bT, (1.51)
' и ii и h — эмпирические константы.
()по имеет почти гу же область применимости.
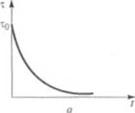
При очень низких скоростях сдвига большинство неньюто - ппнеких жидкостей обнаруживают ньютоновское попедение. )ин >ффект представлен на рис. 1.8, где логарифмическая кривая Iечения становится прямой и (в виде графической зависимо - in Igpo от 1/7), как и предполагалось, описывается уравнением < I ’<>). Заметим, что в данном случае точки хорошо ложатся на ч>ямую линию. На рис. 1.9 показаны те же самые данные, пред-
нменные в виде графической зависимости lgp0 от /', описывае - ||>п. как предполагается, уравнением (1.51). Заметим, что сушение г некоторая кривизна линии, проведенной через точки, полу - I иные для полиэтилена, однако в относительно узком интервале
1,8 2,0 2.2 2.4 2,6 2,8
1000/Г. К"1
360 400 440 480 520 560
Г К-1
Рис. 1.8. Зависимость ирслсльной ньюго - Рис. 1.9. Зависимость вязкости от аб*
|
ной температуры: |
мовской вязкости от обратной абсолют - солютной температуры:
а - полиэтилен низком плотности
а - полиэтилен ниткой плотности: б - (П')ВД); 6- поливииилбутираль
полипииплбушраль
температур полученные кривые для большинства технических целей можно принимать за прямые.
Данные по течению для большинства промышленно важных термопластов собраны Вестовсром |3|. Им была изучена зависимость вязкости ti от температуры при постоянной скорости сдвига.
|
р, яехр(-Л,7])
|
|
или в эквивалентной форме: Р1 = р2 ехр[6, (Ъ - Т)] = р2 ехр(й, д Т). Замети м, что когда ДТ =/Ь.(, |
Величина 1/fy показывает, на сколько градусов нужно увеличить температуру полимера при постоянной скорости сдвига, чтобы вязкость уменьшилась в 1/е раз. Чтобы показать это, запишем выражение (1.51) в виде
Следовательно, смысл значения l/fy раскрыт.
11сньютоновская вязкость г| является функцией деформации t пипа (так как характеризуется значениями у или т), так же как и функцией температуры. Это выражается функциональными уравнениями:
|
П = п(с7*); п=л(у.'0- |
|
(1.52) (1.53) |
|
Следовательно, когда известно изменение п с температурой, представляет интерес исследование изменения вязкости при по - » тинной скорости сдвига или при постоянном напряжении сдви - i. i Вообще, (<)?i/c)7')t не должно равняться (^л/д’О Каждый тип п 1менсния дает различные значения энергии активации. Бестуль и Ьельчер |4| теоретически показали, что для псевдопластичных ♦ ид костей ran |
|
fan i)T |
|
Полный дифференциал п. считая, что п является функцией т и / . равен: |
|
(1.55) |
|
Для процесса, протекающего при постоянной скорости сдвига, уравнение (1.55) может быть записано так: |
|
(1.56) |
|
(1.54) |
|
э т |
|
dn |
|
дц дТ |
оно может быть преобразовано:
{Эг/дТ | far
|
(1.57) |
|
дх |
(Эп/ЭГ^ =
Ыфференцируя уравнение (1.11) по п при постоянной у, по - 1УЧИМ выражение
(!).=* (1.58)
• иорос приводит уравнение (1.57) к виду:
|
m |
|
(1.59) |
(Эп/ЭГ) ran
(дц/дТ).
По определению, псеваопластичной жидкостью является жидкость, для которой л уменьшается при увеличении х. Следонательно, ((h/<h)r отрицательно, а правая часть уравнения (1.59) должна быть больше единицы. Таким образом, неравенство (1.54) доказано.
Предполагая, что температурная зависимость ц может быть выражена через уравнение типа уравнения Аррениуса (1.50), имеем:
^AeE'/RT, r) = AeF-i/RT. (1.60)
Первое уравнение относится к изменениям вязкости, которые проявляются при постоянном напряжении сдвига, а второе — к изменениям, которые имеют место при постоянной скорости сдвига. Значения и Щ определены Филипповым и Гаскинсом для полиэтилена в интервале температур от 108 ‘С до 230 *С. Они приведены в табл. 1.2 |1|.
|
Габлки а 1.2. Энергии активации течения для ihmh:>имена я температурном нмкрвале 108—230 ’С
|
Заметим, что при очень малых напряжениях сдвига энергии активации остаются неизменными. Этот результат можно предсказать на основании уравнения (1.59) подстановкой частной производной из (1.60):
in.') finl - п£у
ЭГ JT RT2’ [drjj RT2 <l*6l>
При этом получим выражение
|
|
которое показывает, что £т становится равным Гу, когда у стремится к нулю. Этот общий результат применим ко всем жидкостям. Для ньютоновских жидкостей Ех равно Гу при всех условиях, так как (Эп/Эт)у. =0.
Вязкоупругими называются жидкости, проявляющие как упру - iiie (упругое восстановление формы), так и вязкие свойства (вяз-
• <*о гсчсние). Для того чтобы лучше понять физическую природу (.них жидкостей, можно их условно представить состоящими из «и н п. мых механических элементов, которые в совокупности мо - и- шруют действительное поведение жидкости при течении. Слс - Iус I при этом отметить, что между поведением механических мо - I псп и истинными физическими свойствами жидкостей наблю - ыпся только отдаленное сходство.
11Я моделирования обычно используются три механических
• к-мента:
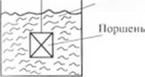
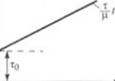
I Модель ньютоновской жидкости - вязкий элемент, пред - « IЩ1ЯЮШИЙ собой сосуд, заполненный ньютоновской жидко - M. KI, в которой перемещается поршень. Поршень перемешается no I юйствисм силы /-'(рис. 1.10, а). При условии, что система об - | i. ii г идеальными свойствами, т. е. что влиянием турбулентности. . н ими тяжести и инерцией, а также концевыми эффектами мож - мо пренебречь, сила Fприведет к возникновению в жидкости напряжения т, которое заставит жидкость деформироваться с постони юн скоростью сдвига. Если F(а значит и т) увеличить в 2 раза, и. скорость сдвига жидкости и скорость подъема поршня также мк'ямчатся вдвое. Если мгновенно снять силу F, то поршень нс - и - пенно остановится и не будет стремиться вернуться в первона - I I п. пое положение. Таким образом, модель обладает основными я ргами чисто ньютоновского поведения: линейной зависимое - н. ю между напряжением сдвига и скоростью сдвига и отсутствием памяти» или какого-либо предпочтительного состояния системы.
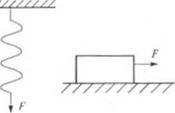
2. Модель Гука. Идеальная упругая пружина моделирует упру - ioe гвердое тело (рис. 1.10, 6). В этом случае инерционными силами глкже можно пренебречь. Под действием силы F пружина ммншенно удлиняется, причем величина растяжения прямо про-
|
|
|
Ш кии безтрснин Г |
|
жидкость |
|
а |
|
Рис. 1.10. Реологические модели различных тел |
|
|
|
п |
|
и |
|
|
|
Низкая ньютоновская |
порциональна /•'. Как только напряжение снимается, пружина мгновенно возвращается в свое первоначальное положение, демонстрируя тем самым прекрасную «память* о своей предпочтительной конфигурации.
3. Модель Сен-Венана (рис. 1.10. в), которая может быть представлена элементом, лежащим на плоскости, иллюстрирует некоторые свойства жидкости. При этом полагают, что элемент не обладает инерцией, а статический и кинетический коэффициенты трения равны.
Характерно, что тело не начнет двигаться до тех пор, пока величина напряжения не превысит некоторого предельного значения.
Вместе с тем рассматриваемое тело может двигаться с любой скоростью, когда приложенное усилие достигнет или превысит величину, соответствующую предельному напряжению.
Простые модели Максвелла и Кельвина—Фойгта. Основываясь на этих трех механических элементах, можно рассмотреть поведение нескольких типов более сложных жидкостей.
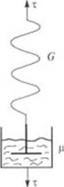
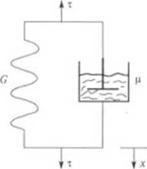
Модель Максвелла. Максвелл в 1884 г. предложил для описания свойств реальных тел модель, состоящую из идеальной пружины и вязкого элемента, соединенных последовательно (рис. 1.11). Как только к такой модели прикладывается напряжение т, пружина мгновенно растягивается. Под действием того же напряжения поршень начинает двигаться в жидкости с постоянной скоростью, пока величина т поддерживается постоянной.
Общая деформация, таким образом, будет равна сумме дефор - мации пружины и деформации, обусловленной перемещением.
Для вывода реологического уравнения состояния рассмотрим геометрический, кинематический и физический аспекты задачи.
|
Рис. 1.11. Простая модель Максвелла |
(.Геометрический аспект. Применим метод сечения. Дтя того чтобы система находилась в равновесии, необходимо отброшенную часть заменить силой. Из рассмотрения равновесия тела имеем (7):
т = тн; (163)
t = tn, (1.64)
где Тц — напряжение элемента Гука; tn. — напряжение элемента Ньютона.
2. Кинематический аспект. Общая деформация тела равна сумме деформации элементов Гука и Ньютона:
Yv=Yh+Yn - (1.65)
3. Физический аспект. Рассмотрим взаимосвязь деформации и напряжения в каждом элементе:
т = 6>„, т„ т. Y” = G=G’
11ч цемента Ньютона
YN=^L = -. (1.67)
И M
Дифференцируя уравнение (1.65) но времени, получим: dvv dy,, dyN
И $ закона Гука для сдвига (уравнение (1.66)] имеем:
dyH 1 dxH 1 dr Yh " d/ G <t * Gdi‘ <L69)
И { уравнения Ныотона получим (см. уравнение (1.67)|:
dyN tn т
(|'70)
< учетом (1.69) и (1.70) из выражения (1.68) получим следую - |||.v реологическое уравнение тела Максвелла:
1 dx т
Yl“cd7+i? (К7|)
I in исследования поведения тела при деформировании необходимо решить дифференциальное уравнение (1.71). Для этого р. ь i мотрим следующие режимы деформирования.
А Постоянная деформация. В этом случае dyv/d/ = 0. Тогда чмннсние (1.71) приводится к следующему виду:
dx <7 .
57=-/'- (1.72)
• v ia интегрированием получаем:
Jdx G'. . х Gf
J —=—/d/; In —=—/;
to T Bo t0 p
T = t0exp(~/1 (I73)
В
напряжение, которое существовало в момент прекращения деформации.
Таким образом, напряжение т уменьшается в е раз (- на 37 %) (рис. 1.12, а) по сравнению с первоначальным значением за время, при котором
|
67/ц |
(1.74)
Выражение Л„=р/6 имеет размерность времени и называется временем релаксации напряжения.
Б. Постоянное напряжение, т. с. т = const и dx/dt = 0. Тогда уравнение (1.71) имеет вид:
|
(1.75) |
dyv т
Интегрирование последнего уравнения даст нам следующее выражение:
Yl=^' + C. (|.76)
Постоянная интегрирования С находится из начального условия у = Yo при t = 0, откуда С = Yo - Тогда
|
(1.77) |
Yi =Yo +—/• й
Графическая иллюстрация уравнения (1.76) приведена на рис. 1.12, б.
Такое поведение рассматриваемого тела объясняется тем, что пружина в момент приложения напряжения немедленно удлиняется до своей конечной длины. После этого движение всей системы зависит только от поведения вязкого элемента.
Если к телу Максвелла приложена знакопеременная нагрузка, то при достаточно высокой частоте изменения напряжения поршень практически не будет перемешаться и тело в целом проявит только упругие свойства, т. с. превратится в идеально упругое тело.
|
|
|
|
'Х&У' I Разгрузка
£
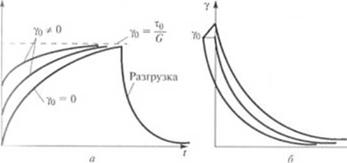
Рис. 1.12. Графическая иллюстрация повеления тела Максвелла при различных режимах .(сформирования:
а - постоянная деформация; Л - постоянное напряжение: в - полное снятие напряжения
В. Полное снятие напряжения. В этом случае т = 0, a dt/dt * 0. Пила из уравнения (1.71) получим:
|
dyv _ 1 dx d / Gdt' Gyv = т. |
|
(1-78) (1.79) |
|
И III |
Уравнение (1.79) представляет собой результат дифференцирования уравнения Гука. т. е.
т
y~G
I рафическая иллюстрация поведения тела Максвелла пред - « имена на рис. 1.12, в.
Пружина мгновенно сокращается до своей первоначальной пипы, а поршень останавливается. В результате тело в целом ос - мстся деформированным на величину, равную перемещению поршня вязкого элемента. Поэтому тело Максвелла иногда называют «жид кообра зн ы м ■».
Модель Максвелла описывает только мгновенную упругость, и«- наблюдаемую в реальных полимерных материалах.
Модель Кельвина— Фойгта. Это тело можно представить состоящим из вязкого и упругого элементов, соединенных не лослсдова - н* п. по, а параллельно.
|
|
|
(180) (1.81) |
|
Рис. 1.13. Простая модель Кельвина— Фойгта |
Под действием приложенного постоянного напряжения тело начнет деформироваться, т. е. вначале пружина растянута незна - штсльно, ее реакция относительно мала и большая часть напри женин приходится на вязкий элемент. Для получения рео- юшчсского уравнения тела Кельвина—Фойгта опять рассмотрим геометрический, кинематический н физический аспекты задачи.
Из геометрического рассмотрения займи имеем (рис. 1.13):
Тг - tn + т„, и I кинематического:
ys=yhsyn; и. фи зического:
=Yh^ = Yj:(?;
|
(1-82) |
dyr
= HYn
С учетом выражения (1.82) из уравнения (1.80) получим:
dv
т, =yhC + HYn =Y^ + H-^-. (1.83)
или
^■Yt + ^Yi - (1.84)
Выражение (1.84) является реологическим уравнением простой модели Кельвина—Фойгта.
Для исследования поведения простой модели Кельвина—Фойгта при произвольных режимах нагружения необходимо решить последнее дифференциальное уравнение. Для этого рассмотрим режим деформирования при постоянном напряжении (ползучесть), т. е. t = tq = const.
Тогда уравнение (1.84) примет следующий вид:
dYv то A. v^ G( to')
или
_d(YE-VG) = --d,. (,.86,
Интегрированием уравнения (1.85) в пределах от у0 до Yx полу
|
откуда |
чим:
In h~Xo/^ = --ine, Чо-Ч/G И
|
или |
|
(1.87) |
-£f 1-е »*
Уравнение (1.87) характеризует изменение величины деформа - ции во времени при постоянном напряжении.
Из этого уравнения следует, что при / = 0, у - уо > а при / = со yv = T0/G, т. с. простая модель Кельвина—Фойгта ведет себя как мЪдель Гука.
Графическая иллюстрация уравнения (1.87) представлена на рис. 1.14.
При разгрузке (мгновенное снятие приложенного напряжения) имеем:
т0 =0.
|
|
|
I «ила уравнение (1.87) принимает вил |
(1.88)
| < «.‘формация определяется первым членом уравнения (1.87) (pm 1.14, 6).
При постоянной деформации Yr = Yo - const, т. с. dyv/dt = 0. I"i i. i уравнение (1.84) принимает вид
|
Т |
"1К 1Л
• ■ реологическое уравнение вырождается в закон Гука. По в от - Iн*11ю or элемента Гука конечная равновесная величина деформации при приложении напряжения достигается не мгновенно, а по им шжении определенного времени. После снятия нагрузки деформация исчезает не мгновенно, а постепенно (рис. 1.14, а).
>io явление называется зопаздывающей да/юрмацией, или упругим последействием, а отношение р/6* = /3, имеющее размерность мргмепи, — временем запаздывания.
ОГмзбтенные модели Максвелла и Кельвина—Фойгта, Простые note «и Максвелла и Кельвина—Фойгта не всегда оказываются ик мточными для исчерпывающего описания поведения реальных полимерных материалов. Чтобы распространить данные мо - н hi на более сложные системы, близкие к реальным жидкостям,
• и мыиастся удобным рассматривать ряд простых максвслловс-
• и «цементов, соединенных параллельно, либо в послело ватсль-
|
!'"• I 14. Графическая иллюстрация повеления просюй модели Кельвина—Фойпа мри |'.i гшчных режимах деформирования: ■сформирование при постоянном напряжении; б - мгновенное снятие напряжения |
|
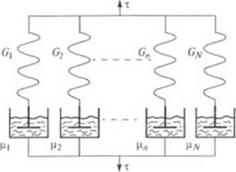
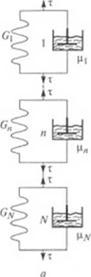
Рис. 1.15. Обобщенные модели вязкоупругих жидкостей: и - Кельвина—Фойгта; б — Максвелла |
|
|
ную цепь фойгтовских элементов (рис. 1.15, а, б). Такое соединение используется потому, что параллельно соединенные максвелловские элементы проявляют те же свойства, что и одиночный элемент Максвелла, и последовательное соединение элементов Фойгта ведет себя подобно простому фойгтовскому элементу.
Реологическое уравнение обобщенной модели Максвелла находится из рассмотрения системы, состоящей из N параллельно соединенных максвелловских элементов (рис. 1.15, б).
Для /»-го элемента связь между напряжением и деформацией выражается в виде
т„ 1 dt„
(1.90)
где т„ - напряжение сдвига л-го элемента; ц„ - вязкость л-го элемента; 6'„ - модуль сдвига л-го элемента.
Полное напряжение т(/) будет суммой отдельных составляющих:
т(0= £>(')■ (1.91)
1»о|
Следовательно, если рассмотреть систему из N элементов, подвергнутую в начальный момент времени (/ =0) деформации у0, остающейся затем неизменной, то убывание напряжения во времени
(1.92)
|
|
|
<»vют происходить в соответствии с уравнением (1.73) п I |
|
/ |
|
| и время релаксации //-го элемента обобщенной модели Максвелла. |
В пределе, когда N = ос, константы G„ и кр„ заменяются функцией распределения С(ЛР), которая представляет собой модуль ум Ругости, связанный со временем релаксации Лр.
( юдовательно, при /V =«> получается зависимость
/
|
(1.93) |
x(/) = Yo?^(ap)^ /pdXp.
о
представляющая собой реологическое уравнение обобщенной максвелловской жидкости. Для обобщенной максвелловской мо - | in вводится понятие функции релаксации у(/) вязкоупругого м. нериала, определяемой как отношение напряжения, выраженной) в виде функции от /, к начальной деформации при условии, •но материал подвергнут мгновенной деформации у0 в момент времени t = 0:
(194)
|
v(/) = t(/)/yo- I огда для обобщенного максвелловского тела получаем:
|
величину (7(ХР) можно определить из релаксационных изме - Р ими. Реологическое уравнение обобщенной модели Кельвина Фойгта получается аналогичным образом. Для этого рас - мофим последовательную цепь из N фойгтовских элементов (рис. 1.15, а).
В модели Кельвина—Фойгта п-й элемент характеризуется мо - iv к’м сдвига G„ и вязкостью ц„. Тогда время запаздывания этого
• « мента л-,,, равно in/G„. Пусть напряжение ти, внезапно прило-
• иное в начальный момент (/ = 0), остается затем неизменным.
I hi п-го элемента из формулы (1.87) с учетом того, что уо = tJG„, получим:
/
|
|
(1.96)
Полное смещение системы у будет суммой деформаций отдельных элементов:
|
( 1 ) |
||
|
1 |
5 г 1 |
|
|
. |
^ / |
|
/V Y(') = t0X л= 1 |
|
(1-97) |
Обычно принято обозначать 1/(7,, = /„, где 1„ — податливость сдвигу.
|
(1 98) |
Тогда
|
1 |
||
|
<п |
S ■< 1 |
|
|
к '4 |
|
N Y(0 = ioX Я=1 |
При Л' =«» приходим к бесконечной цени элементов, для которой времена запаздывания изменяются непрерывно от нуля до бесконечности. Конечное число постоянных для элементов /,„ А31, теперь заменяется функцией распределения /(А,,,). которая представляет собой упругую податливость, связанную с временем запаздывания Азп, рассматриваемым как непрерывный параметр. Обычно эту функцию называют распределением времени запаздывания.
При переходе к пределу Лг-> уравнение (1.49) записывается в виде
I
|
Лл, |
|
|_е |
|
(1.99) |
|
31 г |
|
у(О-т0 И(лзп, о |
Использование понятий функций распределения времени и распределения податливости /(Л,„) весьма упрощает описание реологического поведения материала. Такой метод нашел успешное применение при изучении аморфных линейных полимеров.
Для обобщения фойгтовской модели вводится понятие функции ползучести вязкоупругого материала, определяемой как отношение деформации, выраженной в виде функции от /, к напряжению при условии, что к материалу после релаксации внезапно приложено постоянное по величине напряжение.
Если деформация у (0 получается после приложения напряжения т0 в начальный момент времени (t = 0), то функция ползучести будет равна:
ф(')=—• (1.100)
т0
|
|
|
Гогда из уравнения (1.99) для обобщенной модели Фойгта получим: |
|
(1.101) |
п распределение времени запаздывания /(л,„) можно определить на основе найденной экспериментальным путем ползучести ф(/).
Кроме рассмотренных выше существует еще множество смешанных моделей (тела Бюргсрса, Пойнтинга—Томпсона, Шведова—Бингама и др.), предложенных различными исследователями а 1я описания повеления реальных тел.