Теория и практика экструзии полимеров
УРАВНЕНИЯ НЕРАЗРЫВНОСТИ, ДВИЖЕНИЯ И ЭНЕРГИИ
Уравнения неразрывности, движения и энергии представляют собой математическую формулировку основных физических принципов и не зависят от природы жидкости. Уравнения, описывающие процессы течения, всегда являются следствием этих уравнений, рассматриваемых совместно с реологическим уравнением жидкости. В этом разделе они приводятся без доказательства и используются для краткого математического вывода уравнений течения.
Рассмотрим некоторую область в пространстве, занятом движущейся вязкой жидкостью. Плотность жидкости р, давление Ри температура Тявляются скалярными величинами; скорость жидкости v является векторной величиной, в то время как величина г, представляющая собой результат действия вязких сил, есть симметричный тензор второго ранга. В дальнейшем эти величины рассматриваются как функции времени и пространственных координат.
Рассмотрим произвольный элемент жидкости, расположенный внутри воображаемой замкнутой поверхности, которая движется вместе с элементом, но не оказывает на него воздействия. Элемент жидкости представляет собой термодинамически замкнутую систему. т. е. такую систему, которая может обмениваться с окружающей средой энергией, но не веществом.
Из закона сохранения вещества следует, что масса в замкнутой системе остается постоянной. Уравнение неразрывности 11, 5, 6|
(/ - время) является математическим выражением этого закона.
Согласно второму закону Ньютона, изменение количества движения элемента жидкости равно сумме всех сил, действующих на пего. Математическое выражение этого утверждения есть уравнение движения:
p^- = -(V/>) + (Vx)+px, (1.2)
l ie r — главный вектор массовых сил (сил, приходящихся на единицу массы), ийствуюших на жидкость в рассматриваемой точке.
Из первого закона термодинамики (закона сохранения энер - |ии), примененного к элементу жидкости, следует уравнение мер-
гии:
’Cv^ = -(V «)-4fJ] (V v) + (t:vvyf, (13)
А
Р
l ie Cv — удельная теплоемкость жидкости при постоянном объеме; А —термический эквивалент работы; </ —вектор теплового потока, связанный с градиентом к-мпературы и изотропной среде законом теплопроводности Фурье:
? = -*(VT), (1.4)
i .ic к - коэффициент теплопроводности жидкости.
Компоненты вектора теплового потока в прямоугольной, цилиндрической и сферической системах координат представлены в мол. 1.1.
Векторная форма, в которой были записаны уравнения неразрывности, движения и энергии, имеет перед скалярной преимущество, состоящее в краткости записи и независимости от выбора системы координат. Однако при решении конкретных задач течения необходимо выбрать систему координат и определить в ней компоненты векторных и тензорных величин. Выбор системы координат зависит от геометрии границ жидкости.
|
I а б л и ц а 1.1. Компоненты вектора теплового потока
|
Ниже приведены уравнения неразрывности, движения и энергии в прямоугольных, цилиндрических и сферических координатах.
Уравнение неразрывности Прямоугольные координаты (х, у, г):
t+£(pv'>+£(p‘V)+£(pv‘)=0-
Цилиндрические координаты (г, 0, г):
l+;|;(p^)+;l(p, b)+&pv*)=a
Сферические координаты (г, 0, <р):
— + - у—lpr2v )+ —I——(р^с, sino)+—г------ — (pv ) = 0.
dt г-дг У ' rsinoao rsinoatp1
|
+v |
+ v ^ |
+ V^1- |
dP |
fdXxx |
dlyX |
■ |
|
|
Pi * |
x Эх |
y dy |
<dz) |
Эх + |
dx s. |
dy |
dZ |
|
Уравнение движения в прямоугольных координатах Проекция на ось х: |
|
+ P Их- |
|
dvv dvv £- + v |
dv., + V |
dvy + v f |
dP |
(foxy |
,8t» |
|
|
dt X dx V |
У dy |
z dz У |
dy |
dx |
dy |
dz |
|
Проекция на ось у. |
|
Проекция на ось z'. |
|
My |
|
dvyy + dz^ dz |
|
Mz |
|
dt |
|
dx |
|
Ъ.+„ i^+v ^+v 2V|--^+fe.+ + V" + V'3y+V* Эг ' Эг + Эх + Эу |
Уравнение движения в цилиндрических координатах Проекция на направление г:
TOC o "1-5" h z ' j *
|
dP dr + |
Эу, dvr v0 dvr 'q dv.
—L + V/. _JL + _Li L _ _У_ + Vt _JL
dt dr r dO r dz
|
+ P Xr |
dr r dO r
rdr r dO r dz
|
dva ) I dP |
Проекция на направление 0:
dvn 3v„ vn Эи» vrv,
|
ЭУт ■ + V - —^ - Эг |
ЭР |
|
Эг |
|
|
с |
+Р£г* |
|
Эг |
|
Эу. Эу. у0 Эу. —^- + у-—S - + -2—± Э/ ' Эг г ЭО Г » Э, V 1 Эх0 +Ьэ7^)+7м |
|
р( |
|
Проекция на направление с |
Уравнение движения в сферических координатах Проекция на направление г:
|
ЭР Эг + |
Эуг _ и Oiv, у0Зуг, уф Эу,
■+ У|
Э/ г Эг г 30 г sin 0 Эф
|
I ^лр Т00+Тфф |
|
“Т~(г2т/г)+—г—^-(х^sinO). г2 Эг' / rsinO ЭО rsinO Эф Проекция на направление 0: J ^ + v Jv’° ■ v° dv° i V<p Эу° . V^V,> y»Ctg° I Э/ r Эг r 00 rsinO Эф г г 1 Э / 2 1 ^ / • Л 1 ^Ор х*, ctgO ——(r‘Twi 1 + —:——(xor)Sin0) +—:-------------------------------------------- -22. + - S. —x, r2 Эг' ' rsmОЭ0 rsinO Эф г г Проекция на направление ф: Эуф Эуф v0 Эуф уф Эуф уфу, у0'-ф |
|
+ Р&-- |
|
1Э/>| гэе+ |
|
+ РЯо- |
|
1 ЭР rsinO Эф + Р£р- |
|
- ■+ у-—- + ——^- +—г—г*^” + - z~~~ + ——^-CtgO Э/ Эг г ЭО rsinO Эф г г |
|
ЭТп,, + | Эх, |
|
w | тгф t 2ctg0 ^ |
|
Ор |
|
r2 3/-V г ЭО |
|
rsinO Эф г Уравнение энергии |
|
Э^у L, _____ 1_ О. |
|
|
[эх |
Г I Эд' |
|
Эу |
|
|
1х * Э^ |
|
|
Эу., |
|
|
+ хк ✓ |
~э? + Ч |
|
+ л! т |
|
XX |
|
—±.+—£. Эг Эх |
|
г а Эг |
|
( Э/ Д дх ду Эг |
|
Эу,- ^ Эуу |
|
+ /I Х«, |
|
*4 Э^ Эх |
Цилиндрические координаты (/*, 0, г):
1 а (гп w1 + э<?г
|
аг + г ае |
|
Эг |
|
1Эу. ^dv0 \ |
||
|
[ Щ г ) г ЭО |
дг + Эг J+T°‘ |
г до dz /» |
|
trfap'sftd, V 1 dvG dv*' t ЭГ |> L Г Эт(n> *+ г "00 f IT. |
|
+ Л |
|
8vr I T, r ~дг + т°° г |
|
tbj) 80 |
|
■ + v, +t7 |
Сферические координаты (г, 0. ф):
|
р Cv I д |
(дТ дТ v0 дТ v ЭТ)
— + у — + —------ + —
Э/ дг г Э6 rsinO Эф
|
) rsinO Эф I |
= - - т“-(^г)+—*—-^-(<fosinO) + | г2 3r' r> rsinO 80 '
1 Э
Эи.
(v0sinO) + rsinOЭО rsinO Эф
.[ dvr TI3v0 vr
+А[ъ^+ъ[т£+тг
1 Эи0 УЛ u0c/ge rsinO Эф г г
|
Эи, Эг |
|
0+1^._^|+т |
|
+Л |
|
А? |
|
1 Эу0 ctgQ |
|
+Т, |
|
г ЭО г (Ву г ЭО rsinO Эф г |
|
I dvr Эг rsin 0 Эф |
|
ГЭн» |
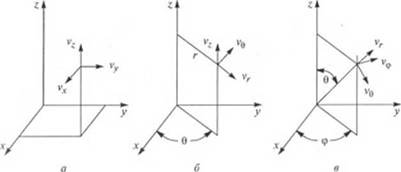
На рис. 1.1 показано, как определяется положение точки к пространстве в каждой из трех указанных выше систем координат, а также направление компонент вектора скорости v в данной точке. Например, в цилиндрических координатах компонента скорости v0 перпендикулярна плоскости, образованной направлениями г и Z-
Девиатор тензора напряжений т, являющийся тензором второго ранга, имеет компоненту т, у, где /' и j независимо принимают значения ху у и z. Второй индекс определяет направление действия напряжения, а первый — направление нормали к поверхности, в которой оно действует. Например, хху представляет собой напряжение, действующее в направлении оси у в плоско-
|
Рис. 1.1. Компоненты вектора скорости V в прямоугольных (о), цилиндрических (й) и сферических («) координатах |
cm, перпендикулярной к оси х. Вследствие симметрии тензора т,
т. е.
xii =туЬ 0-5)
юлько 6 его компонент являются независимыми.
В общем случае движение жидкости не может быть полностью определено только с помощью уравнений неразрывности, движения и энергии. Поэтому возникает необходимость и реологическом уравнении, связывающем компоненты тензора напряжений с компонентами тензора скоростей деформации жидкости, а для случая, когда плотность не может предполагаться постоянной, требуется и уравнение состояния. Дополнительно может потребоваться уравнение, определяющее зависимость температуры и давления от некоторых других свойств жидкости.