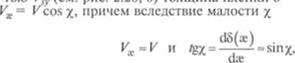Теория и практика экструзии полимеров

СМЕШКИ И К ПОЛИМЕРОВ В ЗОНЕ ПЛАСТИКАЦИИ (ПЛАВЛЕНИЯ)

В работах |13, 49) при экспериментально-теоретическом иссле - ювании процессов смешения в одношнековом экструдере показа­но, что:

1) вклад пленки, в сравнении с жидким ядром, в процессе сме­шения значителен: расстояние между черными полосами в этих областях — одного порядка;

2) степень смешения в жидком ядре чрезвычайно неоднород­на, так что, характеризуя ее, недостаточно пользоваться только одним параметром (например, толщиной полосы г или величи­ной деформации /'{см. формулу (2.236)|; необходимо вводить ха­рактеристику распределения этой величины (например, диффе­ренциальную или интегральную функцию ее распределения 156));

3) расплав, протекающий из жидкого ядра последующего вит­ка через гребень нарезки, проходит сложный путь деформирова­ния (см. рис. 2.28) в пленке, в жидком ядре, затем, перетекая че­рез гребень, снова в пленке предыдущего витка; таким образом, степень смешения его гораздо больше, чем основной массы рас­плава.

>ти особенности следует учитывать при количественной оцен­ке смесительного воздействия переходной зоны.

Процесс плавления полимера в переходной зоне имеет место в основном на границе раздела у = 0 (см. рис. 2.28) между тонкой пленкой расплава и твердым полимером за счет передачи тепла от «зенки цилиндра и диссипативных тепловыделений в пленке.

Поступающий из твердой области в пленку со скоростью Vsy рас­плав увлекается из нес стенкой цилиндра и скапливается у толка­ющей стенки канала шнека, образуя область расплава шириной (IV— К). Вследствие расхода расплава из пленки уменьшается ширина К твердой зоны, перемещающейся вдоль канала со ско­ростью Vr. При z = Zk процесс плавления заканчивается. В соот­ветствии с этой схемой смешение расплава начинается с момента поступления его в пленку и имеет место как в пленке, так и пос­ле выхода из нее в область расплава. Механизм движения и. сле­довательно, смешения области расплава практически аналогичен таковому в дозирующей зоне; приближенная количественная оценка степени смешения по величине деформации полимера /' здесь может быть выполнена, например, по предложенной в (481 формуле (2.239).

Для количественной оценки деформации Г, развивающейся в расплаве за время пребывания его в пленке, определим поле скоростей и траекторий частиц в пленке при следующих допу­щениях:

а) жидкость ньютоновская (р = const);

б) течение изотермическое;

в) давление постоянное;

г) жидкость смачивает стенку цилиндра.

Воспользуемся подвижной системой координат х—у, фиксиро­ванной на твердой зоне, причем ;е лежит в вертикальной плоско­сти, проходящей через вектор скорости цилиндра относительно твердой зоны V = УС-УТ, где VQ — скорость цилиндра относитель­но шнека. При наличии расхода через поверхность у =0 со скоро­стью V (см niir 1 ЭХ /Л тпимиия пприь'м Я = 5 (ж), = Ksill X»

(2.241)

Уравнение движения и неразрывности в этом случае имеют вид:

(2.242)

Интегрирование выражения (2.242) при граничных условиях vs| „ =0> veL - V приводит к выражению для поля скоро­стей уж:

*х(У>*)=У

При допущении Viy = const очевидно также, что

5(х) = Д + 2/;х, (2.247)

| дс к ■ Vgf/V.

Вводя в кинематическое соотношение, определяющее уравне­ние траектории

dx dy,

— = _Z = d/t

(2.248)

выражения (2.244) и (2.246) для полей скоростей vx и vy, получаем:

, dx _ dy

6(х) 1

Вводя переменную и = у/б(х) так, что dy = 6(x)dM + //d8(x), на |►сновании уравнения (2.24/) имеем:

кйх иди

(2.250)

Д + 2 кх I-и2

Интегрирование в пределах "|ви8Со = ®- м1а*«*0 =у/Чх)> где. т0 — координата «старта» частицы (см. рис. 2.28, в), приводит к уравне­нию ее траектории:

у«./52(*)-«(*Ж*о). (2.251)

где 5(.т) и 8ц(а-) определяются из формулы (2.247).

Величина деформации сдвига может быть определена выраже­ниями (2.236), (2.237). При учете (dv^,/d;e«dv. e/dy) для рас­сматриваемого случая можно считать y = dv/dr, так что, принимая во

внимание выражение (2.248), величину деформации на выходе из пленки х = К можно определить выражением:

г ?<ЫУ) da-

<2252>

Вводя в формулу (2.252) выражения (2.244), (2.249) и (2.251), получаем:

r,.± f --------------------- ----------- ОХ»

иьы^2(х)-а(х)&(х0) 2к К ) (2-253)

гле ; St

М*о)

Видно, что величина деформации частицы на выходе из пленки зависит от координаты ее «старта», так что истекающий из пленки в область расплава полимер характеризуется целым спектром де­формаций — от Гх j, =0 до Гх 0 = /'пш. Вычислим среднеин­тегральную деформацию на выходе из зоны плавления как

I Г/(У)''х(х>У%е1,к<1У .

Г, =-5-------------------- = -±

5f, о j2 (2.254)

Вводя в У/ и У? выражения (2.253), (2.244) и (2.251), при учете граничных условий (см. рис. 2.28)

т

получаем:

Inf 26-1+2>/б2-б"|^ =

1 к

<&*

у2=_(б*-д).

Из выражения (2.254) видно, что Гг существенно зависит от длины пути, на котором она накапливается в материале, т. е. от величины А', которая, в свою очередь, зависит от координаты дли­ны канала z, отсчитываемой от места начала скопления расплава перед толкающей стенкой канала. Таким образом, полимер, ис­текающий из пленки в область расплава, характеризуется целым спектром Fj (x, z), особенностью которого являются точки rfL0 = ^max и Г А = 0. где Zk — полная длины зоны пластика­ции* г-г*

Элементарная порция расплава, приобретая в пленке деформа­цию попадает в область расплава при координате z и там

накапливает дополнительную деформацию Гор на пути до выхода из переходной зоны (z* - z) таким образом,

(2.258)

Количественную оценку Гор(г) можно производить по формуле (2.240), в которой L — Zk — z и которая для конического канала может быть представлена следующим образом:

те о» - тангенс половины угла конусности шнека.

Степень неоднородности деформации расплава на выходе из переходной зоны удобно характеризовать интегральной функцией распределения типа |F = Q/Q0-Г^, которая определяет долю расхода Qв полном расходе из переходной зоны (?0, имеющую на­пор деформаций от If™ до /V. В данном случае (см. рис. 2.28, а)

Qo — полный расход через канал шнека в направлении z, Q — рас­ход в направлении z через сечение области расплава при коорди­нате z. равный расходу из пленки на участке от z = 0 до z-z, так
что F = F[z), a /V(z) определяется выражением (2.258). Величина (Xz) может быть определена как

0(z)«j^syA(z)dz. (2.260)

о

Значение Q, получим из (2.260) при подстановке в него в каче­стве верхнего предела 1к = *|*-=o*

В общем расходе Q(z) велика доля расплава, перетекающего че­рез гребень нарезки и прошедшего как бы дополнителы1ЫЙ_путь деформирования. Величину этой доли Qul(z), а также ее /V(^) можно определить, пользуясь полученными здесь формулами и несложными соображениями о кинематике движения этой доли.

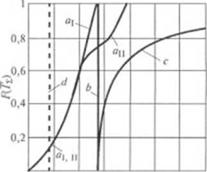
На рис. 2.54 показана функция распределения рассчи­

танная* по формулам (2.260), (2.258), (2.259), (2.254) (кривая а). Для сравнения представлены функции /■(/), определенные для этой же переходной зоны но методам работ |55| (кривая с) и |48| (кривая Ь), не учитывающим влияние процесса плавления на ме­ханизм смешения. Видно, что последние два метода, давая суще­ственное завышение величи­ны /'. не могут быть использо­ваны для прогнозирования степени смешения полимера в переходной зоне. Вместе с тем вклад переходной зоны, более конкретно — областей плен­ки и зазора между гребнем и цилиндром (см. о и с/Ц на рис. 2.54), в общий смеситель­ный эффект одношнекового экструдера значителен (срав­нение кривых а и (I) и должен учитываться при прогнозиро­вании качества смешения.

Наиболее удобной (с точки зрения обобщенности и вмес­те с тем наглядности, «физич - ности» представления) мерой смешения является не величи­на деформации Г, не толщина полосы г (2.235), а «степень утолщения начальной поло-

касчст оыл выполнен для шнека с и = 36 мм, h = 2 мм. и = 17*40'. 1=4 мм. Л = 0,1 мм, при температуре цилиндра 150‘С, частоте вращения шнека N = 70 об/мин.

см», оцениваемая отношением г =г/гц, где г0 — начальная тол­щина полосы. Величина г показывает, во сколько раз уменьши - шсь начальные размеры неоднородностей в материале. Аналити­ческая взаимосвязь между г, г0,г и Г приведена в работе |4|.

Разработанный метод позволяет оценивать степень смешения расплава и характер се распределения в любом сечении потока жидкого ядра в зоне плавления одношнекового экструдера.

Наиболее экономично и наглядно эта информация может быть представлена, например, в виде дифференциальной функции рас­пределения относительной толшины полос г :

M-qT? • <2-261>

1 а* - часть расхода (?(г) » любом ссчснии жидкого ядра, содержащая в себе материал с набором толщин полос от г до г ♦ dr.

Сущность опытной проверки заключалась в сопоставлении эк­спериментально измеренных и рассчитанных спектров для 10 се­чений жидкого ядра переходной зоны.

Толщина полос в сечениях измерялась визуально, с помощью шмерительного окуляра микроскопа при увеличении в 175 раз 49].

Эксперименты в указанных работах проводились на одношнеко - иом экструдере с гладким цилиндром в зоне загрузки и коническим шпеком диаметром D = 36 мм и длиной I. = 20 D, с глубиной канала и и>не дозирования h = 2 мм, а в зоне загрузки h = 5,5 мм. Ширина I ребня нарезки 1=4 мм, а зазор между наружным диаметром шнека и внутренней поверхностью цилиндра Д = 0,1 мм.

Параметры экструзии: температура зоны загрузки Т = 65 С, юмпература стенки цилиндра в зоне плавления Тц. = 130 *С, а час - юга вращения шнека /V = 30 об/мин. Применение конического шнека обеспечивало пленочный режим плавления полимера. Пос - 1с снятия цилиндра со шнека (для этого после выхода на стацио­нарный режим работы экструдер останавливался, а цилиндр со шнеком охлаждался) определялась длина переходной зоны г (зоны п ыстикации), занимающая 6,75 витков шнека и начинающаяся на l. S-м витке (отсчет — от загрузочной воронки, полная. длина шне­ка 20 витков). Срезы выполнялись с шагом z, примерно равным

0,1 г*. Дополнительный срез был выполнен в дозирующей зоне на 19-м витке. На срезах в вертикальном направлении последова - н - и. но измерялись размеры г, каждой толщины полосы. Все г( пе - I«сводились в г{.

Весь диапазон толщин *}(!£/£/) от rmin до разбивался на А интервалов до 16Д^, в которых определялись средние значе-

г-/=ч Г1 г.-ьл-_ bQir-Ги)

• Для /(г)имсстся первообразная функция г'r> )JWr= ,ис.

нм H. ioiuHitc которой возможно, олнако менее наглядно. г*

ния /у, где 1_< j < к. Затем из общего массива г, выделялись груп­пы толщин rij, укладывавшихся в соответствующий интервал

Ary (число гу в интервале Агу обозначим/и,). Величины представлялись дискретно для каждого А Гу как

1 сКЗ I A Sj Q dr S Щ '

Результаты представляли для каждого сечения в виде графика

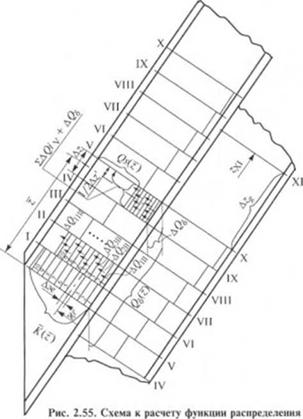
Функция распределения /(г) для условий описанного выше

опыта также рассчитывалась дискретно |13|: вся переходная зона разбивалась на участки длиной &z (рис. 2.55), так что сечения I, II. X, XI примерно совпадали с расположением выполненных срезов. Область твердого полимера в пределах каждого Дz разбивалась на ряд ячеек (от 13 до 4), в зависимости от размеров А'ЫиАа.*. Значения А (г) для сечений I—Vизмерялись на срезах. Для каж­дой //-ячейки с площадью (дг/хЛжу) определяли Д(),. по формуле Vsy(Az х Д;е) и rij по формулам (2.235), (2.258), (2.252) и (2.259). Ве­личину ft определяли как расход через кольцевой канал по фор­муле:

(&(z)=-HcAzsina.

При этом в качестве начальной г на входе в зазор между греб­нем и цилиндром принималась функция распределения /(г) для сечения j + 1, определенная приближенно без учета перетекания

Массив материала / ячеек с участка Дг>, имеющий свою функ­цию распределения, в дальнейшем перемешается в жидком ядре к и мению j + 1, накапливая, в соответствии с уравнением (2.259). юиолнитсльную деформацию на пути Дz и внося вклад в функ­цию распределения для сечения и т. д. Эта особенность также учи­ма валась в расчетах. Таким образом, в этом расчете был прослс - кен деформационный путь каждой /./-ячейки во всей переходной <и дозирующей), вплоть до сечения XI (см. рис. 2.55), зоне.

Дробный niar Да; позволял при графическом построении вы­численной /(г) представлять ее не в виде дискретной, а в виде монотонной функции, как это и есть в действительности.

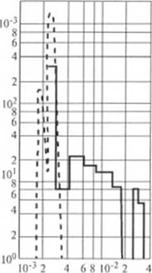
На рис. 2.56 показаны расчетные и опытные функции распрс - к'ления относительных толщин полос f{r). График «Сечение II» соответствует начальной области переходной зоны К = 0,69.

Рис. 2.56. Расчетная и nm. iтан функции распределения толщины полосы г по длине канала (см. рис.

2.55):

I — расчетная: 2 — опытная

«Сечение VIII» — концу ее (Л" = 0,04), «Сечение XI» — концу до­зирующей зоны. Графики для прочих сечений отражают анало­гичную закономерность (13).

Расчетные /(г) имеют две области на ранних стадиях пласти­кации, имеющие разрыв (см. / и 1а на рис. 2.56). Область / с ши­роким набором г и их долей характеризует расплав, деформиро­ванный в пленке и продолжающий деформироваться в жидком ядре; область 1а — расплав, прошедший через зазор между ци­линдром и гребнем шнека и вторично побывавший в пленке. В свя­зи с тем, что величина г у частиц, попавших в жидкое ядро на ран-

них стадиях, продолжает уменьшаться но время пребывания их в жидком ядре, разрыв между областями уменьшается и на поздних стадиях пластикации исчезает совсем. Вместе с тем и правая часть /(/•) по мерс продвижения смешается влево очень слабо, а г ос - 1лются практически неизменными, так как из пленки (более точ­но — из элементарных площадок Дz х Дав со значениями ге, близ­кими к К (см. рис. 2.55)|, продолжает поступать плохо перемешан­ный расплав. После переходной зоны поступление прекращается, и вследствие этого спектр 7 начинает интенсивно сужаться в ос­новном за счет исчезновенияболыиих г.

Сравнивая расчетные /р(г) и опытные f0(7)функции, можно оIметить, что, несмотря на исключительно сложную реальную картину процесса деформирования в пленочном режиме, разрабо - I ап пая методика прогнозирования качества смешения учитывает все ее особенности. Действительно, в тех сечениях, которые нахо - 1М1СЯ в области до начала естественною вырождения пленочного режима (начало — между IV и V сечениями), совпадение /р(г) и /,,(>) вполне удовлетворительное как по г, так и по их долям. На /„(г) можно лаже наблюдать минимум, соответствующий разры - ву /р('‘). Несоответствия в области больших г имеют место не по причине некорректности теории, а вследствие того, что абсолют­ные размеры 7 здесь соизмеримы с глубиной витка и намного больше толщины среза; поэтому вероятность попадания окрашен­ною материала в срез резко уменьшена. Попадание же в срез дает их долю, во много раз большую, чем действительная.

В области вырождения пленочного режима и. особенно, в до - шруюшей зоне, наблюдается несоответствие f0(r) и /р(г). Это вы шало разрушением твердой области на крупные агломераты. Интенсивность их плавления резко падает, и они, будучи плохо перемешанными, достигают области выхода из канала шнека б м. сечение XI на рис. 2.56). На этом графике видно, насколько |инороднее по 7 был бы экструдат, если бы пленочный режим со­хранился до конца плавления.