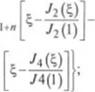Теория и практика экструзии полимеров
РЕШЕНИЕ В НЕНЬЮТОНОВСКОМ ПРИБЛИЖЕНИИ
Процесс плавления полимера в переходной зоне имеет место в основном на границе раздела у = 0 (рис. 2.28, а) между тонкой пленкой расплава ///и твердым полимером, имеющим температуру Г за счет передачи тепла от стенки цилиндра и диссипативных тепловыделений в пленке. Поступающий из твердой области / расплав увле-
I'm 2.28. К анализу процесса плавления полимера в переходной зоне одношнекового
инмрулера:
а - поперечное сечение виитопого камаза: б - развертка винтового каната с векторной •о н раммой скоростей потока: в схема плавления патимера
► дсгея из пес стенкой цилиндра и скапливается у толкающей стен-
► и канала шнека, образуя область расплава //шириной | W АГ(г)|. Кследствие расхода расплава из пленки уменьшается ширина K(z) | вердой зоны, перемещающейся вдоль канала со скоростью У, (рис. 2.28, б). При z = Zk процесс плавления заканчивается.
При рассмотрении движения расплава полимера в пленке примем прямоугольную систему координат х—у (см. рис. 2.27, а, в) с оординатой х, фиксированной на поверхности раздела, которую пт кдствие малости се кривизны будем считать плоской, причем ма юсть углов х |реальные соотношения б(х)/АГ(г)<<10 *| позволя - < I ввести допущение о параллельности поверхности и стенки mini ндра.
Ось х лежит в вертикальной плоскости, проходящей через век - • >р скорости цилиндра относительно твердой зоны v = Vr - VT, где скорость цилиндра относительно шнека. При наличии расхо - I I через поверхность у = 0 со скоростью Уху (рис. 2.28, а) толщина
пленки 5 = Э(х) и Vsy = V sin ж, Vcx = V cos ж, причем вследствие малости х^х =Ktga’ = d6(x)/dx «бшж, так что Vxy = Vd5(x)/dt.
|
(2.32) |
Основные уравнения гидродинамики и теплообмена в этом случае принимают следующий вид |32, 33): уравнение неразрывности:
Эх By
уравнение движения:
|
др |
|
(2.33) |
иг _ дхху _0. Эх ду
реологическое уравнение (при очевидном для данного случая условии Bvx /By »dVy /дх):
|
dvX ду |
|
(2.34) |
|
т |
|
‘ду |
|
т = щ ехр |
|
Т-Т |
( ЭТ ВТ)
уравнение энергии | при учете условия
|
ВТ |
|
Эу% |
|
(2.35) |
|
рСу>'э7=Хэ7+Жду э7 |
|
д2Т |
при граничных условиях
1) З' = 0, vy = V^., v,=0, Т ~ Г (2.36)
2) у = 5(х), vy = 0, vx - К Т= Ть. (2.37) В уравнениях (2.13)—(2.17) приняты следующие обозначения: vx, vy — компоненты линейной скорости расплава полимера
вдоль осей х и у, р — давление расплава; т^ — напряжение сдвига по оси х в плоскости, перпендикулярной оси у, b, т, п — реологические константы; гп0 - значение т при Т = Т Т — текущее
значение температуры расплава; 7" — температура твердой пробки полимера; b = ДЕ/R, ДЕ — энергия активации вязкого течения; R — универсальная газовая постоянная; к — коэффициент теплопроводности расплава; А - термический эквивалент работы; Ть — температура стенки цилиндра; V - скорость цилиндра относительно твердой пробки.
Совместное решение уравнений (2.14) и (2.15) приводит к следующим выражениям для т,,. и vx :
|
■МО М*)‘ |
|
(2.38) |
|
у,(1)6 |
|
и '.(6) |
(лесь и далее J,(J) обозначает /-кратный определенный интег - i*.i I по переменной j с пределами от 0 до j от функции вида
-Ь
схр
я|Г(ф)-7**|* пРичем ПРИ Ф = У»У =^иу = 8, а при р = £ = у/8, / s и j = 1.
Введя выражение для у, (у) в уравнение неразрывности (2.32) и выполняя интегрирование помири граничном условии (2.36) для г, получаем выражение для vy:
|
1 |
|
Му) |
|
dy = |
|
'■(«) |
|
■'.(в) |
|
Эх |
|
*-гМу£ |
|
(У) ,,Ш( d8 (2.39) |
|
1 |
|
,У± Эх |
|
д_ Эх |
|
Э(х) |
|
У,(1) |
|
',(8) |
Определив величину (d6/dx) введением граничных условий ( *7) для vy в уравнение (2.39):
|
м У2(>) |
da ^
dLv V
моаучасм
|
I- |
|
(2.40) |
■Ml)
Введение выражений для vv, хху и dVd, (уравнений (2.40), ( V?8) и (2.34)|, приближенная замена в первом слагаемом
эт ть-Г ду " 5
и допущение о том, что интенсивность диссипативных тепловыдс - КЧ1ИЙ приблизительно зависит от усредненной по площади поверхности раздела толщины пленки
5 = JdzJ5(z, x)dx, о о
приводят к следующему виду уравнения энергии:
|
1+я |
|
ш -ь |
|
I- |
|
■/.О) |
|
(2.41) |
|
^У = о;,(7'4-Г')8К Эуг х ' |
|
х/^61 "схр |
Решение уравнения (2.41) при граничных условиях (2.36) и (2.37) имеет вид:
|
■'i(I) АК) АО) |
|
Т.-Т |
|
■ЛО) АО) |
|
(2.42) |
|
511 |
|
5- |
|
АО) |
|
1+л |
|
где (3 = |
Л V
|
Тепловой поток qy от пленки к границе раздела обеспечивает прогрев полимера, ноступаюшсго из области твердого материала, от Гц до Г*, что математически выражается в виде: |
|
.if") .*(211 |
|
:РСК„(Г*-Г*). п |
|
43) |
|
*У)у-о H^J Определяя из уравнения (2.42) величину (дТ/dt) I ^ 0 и вводя в выражение (2.43), подучаем соотношение между viy и 6: |
|
Л'-О |
|
i+я |
|
МЧ |
|
г - г0 п-т* |
|
Vsy =T°S’ V = |
|
; й = |
|
W |
|
(2.44) |
2 АО)
Интегрирование выражения (dS/dx) по х, где ^(6) определяется формулой (2.44), в которой не зависит от х, при граничных условиях
|
(2.45) |
^>=°-*U=«(*)• «U=8*
приводит к выражениям для 6Х и 6Л-:
|
(2.46) |
_ l2ya3xJi( 1).
[2чгД.^ - МО ^ МО'
|
Из формулы (2.46) можно получить выражение для срсднеин - шральной по х тол шины пленки 6: |
|
2 V«, |
|
|
V |
^C)j |
|
_ | К 2 S = jf8(x)dx = ± |
|
Массовое соотношение, заключающееся в том, что скорость уменьшения расхода твердого полимера через сечение h(z)xK(z) («м. рис. 2.28) в направлении оси z равна расходу расплава из II н ики в область жидкого ядра //, имеет следующий вид: ^г[рЛ(А/0] = - Рт / vxMd* (2.49) d................. ; ...... (2.50) |
|
р Oz о |
|
1 " i»i, р плотность тверлой пробки полимера и его расплава. 11а значительной длине z материал твердой области, будучи до - • точно прогретым, столь уплотнен, что практически монолитен. Мри учете слабой зависимости плотности от температуры будем i. i ice считать, что pr/p = 1. Зависимости vx (£) и 5* (АО представлены формулами (2.38) и Г* 47). Интегрирование (2.50) по z в пределах |
|
У», f 1 |
[ 1 1 |
Z. K = — G = - |
[■/HOI |
|
[21Vj G |
l/Hbj |
w у |
LynoJ |
|
I ш шнека с постоянной глубиной канала h = h0 приводит к зависимости, позволяющей определить длину зоны плавления 'А 'I А' - о' |
|
(2.51) |
|
Однако прежде необходимо определить величину 5, входящую и выражение (2.44) для у. Получив из формулы (2.51) соотношение между dz 11 dA7 d£ = -2_I и »оответствии с определением 5 при учете выражения (2.48) имеем: Дг |
|
(2.48) |
|
•МО ■МО |
|
I < 2Was A V |
|
5 = J5(AT)dz = о |
|
А/щ (2asW |
|
;£= |
|
А = |
|
х(г'-Го) |
|
Т* - Т( |
|
Ц - г _т 2 V 2 ; f = !A |
|
Т' - Гп (2-53* |
(причем Е зависит только от свойств материала) решение задачи, включая формулу (2.51), принимает окончательно следующий
вид:
|
2 W /20) |
|
|
|
0 = /0 = /^+5,-я£ Jl^ |
|
(2.54) |
|
—уЕ |
|
«МО |
|
0). |
|
V = |
|
(2.55) |
|
I+I M) F 2 7,(1) |
|
1 + S|W£ |
|
I 1 + Я J |
|
8j |
|
(2.56) |
|
*>(*) |
где подинтегральная функция в 7, (/) имеет вид exp
|
9Р |
безразмерная переменная 5| связана с ее физическим аналогом соотношением
2Was
> /
Порядок численного решения с использованием ЭВМ сводится к итеративной операции по определению 5| и но (формулам (2.54)—(2.56) при принятии в первом приближении 0(q) = F£ и к последующему вычислению множителя G в формуле (2.51).
Для вычисления значений V и VT (см. рис. 2.28), зависящих от расхода Q, рассмотрим сечение канала шнека плоскостью, пер пендикулярной оси z. Расход через это сечение равен:
|
(2.57) |
Q=vr к.
cos а )
где (/ — е/сош) ширина канала шнека; Л,> - глубина канала шнека в зоне загрузки.
Отсюда находим выражение для Vт:
V - Q
Т (2.58)
^ cosa J
Для определения скорости V цилиндра относительно твердой юны воспользуемся выражением, записанным в векторной форме
п т в скалярном виде:
cosa - (2.59)
Гаким образом, уравнение (2.58) совместно с (2.59) дает иско - мую связь V и Q.
И уравнении (2.54) первое, второе и третье слагаемые представ - ииот собой вклады, вносимые в распределение температуры в и и нке теплообменом за счет теплопроводности, диссипативных и м ювыделений и конвективного теплового потока в направлении у, идущего на прогрев расплава, который поступает от гранимы раздела в пленку расплава.