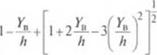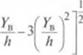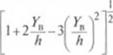Теория и практика экструзии полимеров
РАСЧЕТ СМЕСИТЕЛЬНОГО ВОЗДЕЙСТВИЯ ЗОНЫ ДОЗИРОВАНИЯ одноншккового ЭКСТРУДЕРА С УЧЕТОМ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ВРЕМЕН ПРЕБЫВАНИЯ И НАПРАВЛЕНИЯ СДВИГА В ВИНТОВОМ КАНАЛЕ
Реальный профиль скоростей потока в винтовом канале обус - минивает различие времен пребывания частиц полимера в одно-
• IIисковом экструдере, в свою очередь определяющее спектр тол-
шин полос в готовой смеси. При проектировании экструдеров и математическом описании процессов смешения требуется учет широкого спектра распределения времени пребывания. Для анализа функции распределения времен пребывания обратимся к циркуляции жидкости в плоскости хоу сечения винтового канала (см. рис. 2.57).
Из соотношения (2.266) с учетом, что а| = YJh, а2 — YJh (Yit Уп — координаты положения частиц по оси У в нижней и верхней областях сечения винтового канала), получим:
|
(2.301) |
ПК 0sl'Hs^*,|*sr, s*.
Решение уравнения (2.301) приведено в работе |45| в виде:
|
1 + |
1+3^* Л_
|
(2.302) |
|
1 + |
i+з1; л_
Как уже отмечалось выше, при координате у = (2/3)Л, ямяю - щейся фаницей раздела областей с положительным и отрицательным направлениями v* (см. рис. 2.57), ско|юсть поперечного циркуляционного потока обращается в нуль. Время пребывания частиц полимера в верхней области (с положительным направлением vx) поперечного сечения винтового канала равно
У
(2.303)
|
W |
|
;н = |
|
(2.304) |
|
а в нижнеи |
Тогда время одной поперечной циркуляции находится из выра-
Относительное время пребывания частиц полимера в верхней области канала равно:
W
|
I |
|
в / |
|
МП,) |
|
(2.306) |
|
W W |+ |
|
МП) |
С учетом выражения (2.69) для vx (после соответствующей под-
11. ПЮВКИ Ун и Ув) из последнею уравнения получим:
|
1- |
(2.307)
С учетом тою, что общее время пребывания частицы полимера II олношнсковом экструдере
I средняя ее скорость в осевом направлении \ равна
ic осевая составляющая \ скорости потока находится из выражения |4|
^ = Зл([1]" Л )1 + (P)sinacosa (2-308)
< чесь Vc — пDN — скорость стенки цилиндра), получим:
L
t
(2.309)
Совместным решением (2.302), (2.307) и (2.309) получим общее время пребывания частицы полимера в зоне дозирования одно - шнсковою экстоудепа в виде: I
|
3-Ч--1+3 L h |
,+2H*)T |
|
|
3VC (1 + <p)sinacosa |
1 Г ITT |
|
|
Ll |
, Ун --Я - + |
,+2^-3 (iff |
|
ll |
/I |
h I /» J |
|
L v ' J |
|
/ = • |
|
(2.310) |
t-
|
ЗКС(1 + q>)sinacosa |
■ + SJ I»"* 1 UJ £5 к> 1 |
I |
|
|
1 >и ■ |
2 |
||
|
h |
/» |
h I h J |
|
(2.311) |
|
Функция распределения времен пребывания рассчитывается как |45|: |
П‘)Ч/т (2.312)
причем /■(») =* 1, a tm — минимальное время пребывания.
Для нахождения выражения Д/)с1/ рассмотрим элементарный расход d@ в верхней области на участке Кв и KH + dKB (см. рис. 2.44):
d(?„ = vzlVd Уъ = v. lVhdi ~
|
de»-v^|l + 34»-3^(pjd(^j. |
С учетом выражения (2.77) для v - последнее уравнение приводится к виду:
ТI,+Зф-З^-ф PI ^f-l - (2.313)
Аналогично находим элементарный расход на отрезке К„, Yn + +d)/M в нижней области:
<1QH = МК1КИ =у.1Ш ^
)
После подстановки выражения v. (уравнение 2.77) получим:
d(?„ =K„lW,^l + 34>-3^jd^j.
|
(2.314) |
|
■*{ |
|
+^, + 3ф-зй.<рШ |
|
глс Ус - = nDN cos а — компонента скорости с гонки илоль оси г 206 |
Так как обе указанные выше точки Кв и У„ связаны с тем же временем пребывания частиц полимера между / и / + d/, то распределение времен пребывания является функцией y(/)d/, т. е.
Связь между Yu и YH устанавливается выражением (2.302), дифференцируя которое находим: I
|
+2Нт |
|
1-3^- + п |
|
Y 4 'н |
|
(2.315) |
Совместным рассмотрением уравнений (2.302), (2.314) и (2.315)
|
i уметом, того, что |
|
dlT |
|
получим:
|
|
|
|
1 + 2 |
(2.316)
11равая часть последнего выражения является функцией только YJh, и она же связана со временем пребывания уравнением < 2.311). Поэтому из этих двух уравнений может быть рассчитано распределение времен пребывания и представлено в виде графика инисимости
|
I ■ |
+ ф)
(.' учетом минимального времени пребывания tm частицы с координатой y/h = 2/3, которое легко находится из (2.311), можно и». |учить следующее выражение для относительного времени прерывания любой частицы в винтовом канале одношнскового экструдера: ,
212
|
1 +2-А-3 |
З-^-1+З
И
Y
1 + 2-^ п
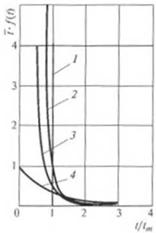
Рис. 2.63. Распределение времен пребывания (РВИ) в смеси гелях различных типов:
|
|
/ — н аппарате идеального вытеснения; 2 — в одно - шнековом экструдере; 3 — при изотермическом течении в трубе; 4 в реакторе непрерывного действия
На рис. 2.63 представлено распределение времен пребывания в зависимости от i/t„ для различных типов проточных реакторов. Видно, что одношнековые экструдеры по распределению времен пребывания занимают промежуточное положение между основными типами реакторов.
Функцию /•(/) распределения времен пребывания можно получить путем подстановки выражения (2.316) в (2.312):
|
1 |
|||
|
3^ |
2 |
||
|
и |
А |
Л [ A J |
|
dl ~h L |
|
(2.318) |
|
|
Интегрированием (2.318) находим:
|
(2.319) |
|
|
На рис. 2.64 представлена графическая зависимость /•(/) от t/tm для различных типов проточных реакторов, откуда видно, что по ti) одношнековый экструдер при t/tm> I приближается к трубчатому изотермическому реактору.
Наличие спектра времен пребывания в сочетании с реальным профилем скорости потока предполагает и различие в величине на-
Гис. 2.64. Заннсимосгь функции РВИ «рот l/lm:
кривые 1—4 - см. рис. 2.63
копленной каждой частицей полимера деформации сдвига. По - иому при расчете деформации сдвига, реализуемой в одношнеко - иом экструдере, необходимо наряду с направлением поля скорое - leii сдвига учитывать также и распределение времен пребывания. II этом случае полная (средневесовая) деформация сдвига, накапываемая расплавом полимера в зоне дозирования одношискового •кструдера, равна 111 :
|
- К Г |
|
(2.320) |
Произведение^ YJh)d( YJh) в правой части последнего уравнения представляет собой долю частиц жидкости, имеющих координату YJh.
В случае двухосного сдвига в направлениях осей х и z деформация сдвига /(YJh) равна:
(2.321)
I! соответствии с картиной циркуляции частиц полимера (см. рис. 2.58) и методикой расчета деформации сдвига с учетом поля скоростей сдвига (см. раздел 2.11.3) имеем:
|
И 1 У, п |
|
Г.( К Л |
|
(2.322) |
|
где |
|
У, • / у„, У, I У,„ |
|
ж |
|
«I Pi |
Тогда с учетом знаков rjYJh) и /'.(Кв/Л), согласно методике расчета, приведенной в разделе 2.11.3 находим:
У, I «1= /
У, п I
+ 1 Dx
|
У".г г + V Их + 1 Шх У, п |
у, и
Если уравнение (2.323) для а] действительно но всех» интервале параметра ф (0 < <р < 1), то, ввиду разнонаправленного поля скоростей сдвига (см. рис. 2.58), необходимо значение р| выводить отдельно для интервалов 0 £ ф £ 1/3 и 1/3 < ф < 1. Тогда согласно рис. 2.58 получим:
1) для режима работы 0 < ф < 1/3
2) для режима работы 1/3 й ф <, 1
Значения Г, х и Гцх, ГШх, Г, Ух находятся так же, как и в разделе 2.11.3, но с учетом координат Кн и Y„. После соответствующих преобразований получим:
|
2tgoLz h |
|
1-3 “I |
|
-2--3 "2 |
|
|2 - 3fl| | -- |
|
|2 - 3«2 |
|
(2-324) |
|
J' _ p ___________________________________________ lx lVx [17 Зф(я2 -1 )]|2 - Зя, I + [ 1 + Зф( я I -1 )]P - 3 a |
|
'1-3]|2-За,|,(1-з)|2-Заг1 |
|
2tg«Z., |
|
h |
|
(2.325) |
|
I 'll* +1II lx ~ ■ |
|
[* +Ma2 " 1 )]l2 - 3«| |+[ 1 + ф( Д, -1 )]|2 - 3a Аналогично можно получить: j. _ L. «2(1 - Зф+6д>ф)|2-3<?2|-tf| О - Зф-6йГ|ф)|2 -3flj| * " T a2a {[1 + 3Ф(а, -1 )]|2 - Зй| |+[1 +3Ф(я, - l)]p -3a2|}' r r Lz a2 О - Зф+6я2ф)|2 -3fl2|-«i (• - Зф+6<7,ф)|2 -3o, | ‘ 2z + 13c - “ “------------------------------------- “• |
|
h a2a {[I + 3ф(а2 -1)]|2 - За, | + [l +3ф(л, -1) i|2 -3«, |}’ L c/2 (1 - Зф+6«2ф)|2-Зд2|-«| (I — Зф—6c/|ф)|2 — 3c/j | h a2a {[l +3ф(«2 — I)]|2 — Зс/, | + [l +3ф(я, - I )]|2 — 3c/21} |
В приведенных формулах Lz — длина винтового канала в зоне позирования.
Полная деформация сдвига в зоне дозирования для режима |) £ ф £ 1/3 равна:
>'//Л
У///к
(2.326)
л для режима 1/3 < ф < 1: - Уп/к
(2.327)
С учетом того, что
|
1 |
|||||
|
3^ |
+ |
1+2-^-3 |
1Уг)2} |
2 |
|
|
// |
и |
А |
|||
|
ту- |
|
dlJI- |
|
(У. |
|
>ГТ |
|
. г* '-f+ |
|
I +2^-3 h |
т
м j выражений (2.326) и (2.327) легко рассчитать величины /’ для различных режимов работы одношнекового экструдера.
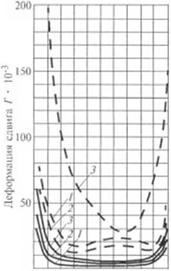
На рис. 2.65 представлены кривые ly/h) =J{y/h), построенные по формулам авторов работ 111. 45, 551. Видно, что для одних и тех же значений коэффициента дросселирования кривые / и 2, построенные по формулам работ |55| и |45], полученным без учета поля скоростей сдвига и циркуляции потока, расположены значительно ниже кривой, построенной по формулам работы (11).
|
0 0,2 0,4 0,6 0,8 1,0 Глубина канала y/h |
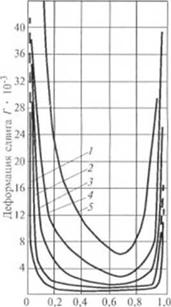
На рис. 2.66 показаны кривые /'(>’//») = Ду/h) для разных режимов (значений ф) работы одношнековых экструдеров. Видно, что наибольшую деформацию сдвига получают частицы, расположенные вблизи боковых стенок винтового канала (y/h равно 0 и I), наименьшую — частицы, которые не участвуют в циркуляции расплава полимера (y/h = 2/3) и, следовательно, характеризуются наименьшим временем пребывания в зоне дозирования одношнекового экструдера. С увеличением коэффициента дросселирования ф величина /'(>’//») резко возрастает. Тот факт, что частицы расплава полимера вблизи стенок канала накапливают наи-
|
Глубима канала y/h |
Рис. 2.65. Сопоставление расчетных Рис. 2.66. Зависимость деформации
шачений /' по формулам Мора |55). сдвига Г от координаты y/h. Значе*
Галмира |45| и Кима |11|: ния ср:
А-0.51 см. /,- 255 см; и-20*С. /-0; 2-0.2: 3-0.4; 4-0.6;
Ф - 0; ф = 0.75 5 - 0.8; L =• 51 см, А — 0.51 см
большую деформацию сдвига, не может существенно сказаться на смешивающей способности одношнскового экструдера, так как их доля в обшей производительности экструдера сравнительно мала.