Теория и практика экструзии полимеров
РАСЧЕТ ПРОИЗВОДИТЕЛЬНОСТИ ЗОНЫ ЗАГРУЗКИ
Основное предположение при анализе работы зоны загрузки заключается в том, что твердые частицы полимера, уплотняясь, образуют эластичную пробку, в которой отсутствуют деформации сдвига. На пробку действуют силы трения, которые возникают между поверхностями пробки, цилиндра и шнека |4, 18—20]. Авторы указанных работ рекомендуют различные формулы для расчета производительности зоны загрузки (питания) одношнсковых экструдеров.
Формула В. А. Силина (19] для случая неравенства коэффициентов трения полимера о поверхности шнека (fs) и цилиндра (/".):
п(D2 - d2 V/ - е)60;У pV
G = —------ -—---------- х
|
(2.3) |
810
|
cos a D cos[ |
ап+(90—р)" |
cos[a,,+(90-p)] |
|
|
:■*) |
cos(90-fi) |
(1 + A)cos(90-0) |
|
|
где G — массовая производительность зоны загрузки; I) — наружный диаметр шнека, (см. рис. 2.13); d — диаметр сердечника шнека; N — частота вращения шнека; t шаг нарезки шнека по наружному диаметру; е — ширина гребня нарез- |
mi шнека вдоль его оси; р — насыпная масса; ц/ — коэффициент заполнения вин - кнюго канала в зоне зафузки; ар — угол подъема винтовой линии по наружному ииметру шнека; urf - угол подъема винтовой линии по диаметру сердечника шнс - ► л. (90 — р) — угол направления движения пробки материала относительно плоскости, перпендикулярной к оси шнека и цилиндра (см. рис. 2.17); к = f-Jf, - отношение коэффициентов трения полимера о поверхности иилинлра и шнека.
Формула В. А. Силина для случая равенства коэффициентов I рения//и/|19|: . .
! я(г> -</ )(/-е)60Л, рч/
С/ ~ ч х
8 -10
|
(2.4) |
cosa^cosfa/, +(90-р)]]_^ cosctj - cosfa,, +(90-P)’J
|
2cos(90 (J) |
(l+^)cos(90-p)
Формула В. С. Рахманова для расчета объемной производи - к-ль мости 0зоны загрузки одношнскового экструдера 118):
TOC o "1-5" h z Q = 2,303lg - nc^- + i(cos2 а0 - cos2 N -
2 sincifl 2' >
sina^ л2 D*tg 3a pig (90 - p)
(2.5)
|
/V. |
^ ^cos(arf + an )sin(arf - a„)+i(arf - a„) Sintt^Sinctj A)
Формула Д. М. Мак-Келви дш расчета объемной производи - 1СЛЫЮСТИ 0 зоны загрузки одношнекового экструдера |4):
|
<? = |
|
IV/u |
|
(2.6) |
|
cosa# + sin(90-p)ctgafl |
|
nDNcosup |
I ie W \ h — ширина и высота винтового канала (см. рис. 2.13).
Формула К. Шнейдера |20| для расчета объемной производи - юльности Q зоны загрузки одношнскового экструдера:
|
(2.7) |
Q. tDHD-kplN ,ea, MZ^
t tga/) + tg(90-p)
Формула Г. Шенкеля |1| для аналогичных целей:
C? = n2Z3/»2(^-/i)Arsina/,cosa/;[l-tgaoctg(90-p)]. (2.8)
89
В. Дарнелл и Е. Мол получили следующее выражение для расчета объемной производительности рассматриваемой зоны |211:
|
(2.9) |
|
|
|
s |
|
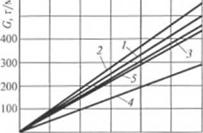
Рис. 2.24. Теоретическая зависимость производи (ельности зоны iaipyзки от частоты вращения шнека |
|
о ю 20 зо об/мин ными исследователями для рас- |
Несмотря на большое число формул, предложенных различ-
чета производительности зоны загрузки одношнековых экструдеров, тщательные экспериментальные исследования это-
го вопроса не проведены. В связи с этим нельзя быть уверенным в том, что выводы этих формул вполне корректны.
Достоверность некоторых из приведенных формул проверена авторами работы |7| на экспериментальном одношнековом экструдере с прозрачным цилиндром (см. рис. 2.15).
Результаты экспериментов с гранулированным ударопрочным полистиролом при свободном выходе (без дросселирования) из зоны загрузки приведены на рис. 2.24. Наилучшее совпадение с экспериментальными данными (график 5) дает формула В. А. Силина (график 3), наихудшее — формула В. С. Рахманова (график 4). Расчеты по формулам Г. Шенкеля (график 2) и Дарнелла—Мола (график /) даюг результаты, завышенные по сравнению с экспериментальными данными (график 5).
П. К. Кленк (22) на основе анализа работы зоны загрузки с цилиндрами различной конструкции получил следующие уравнения для расчета ее объемной производительности:
|
|
I) для гладкого конического цилиндра:
<?= n(D-h)h—+т//) +
глс 5 — радиальный зазор между цилиндром и наружным диаметром шнека (см. рис. 2.13); остальные обозначения — смотри пояснения к формулам (2.3)—(2.9);
выражение (2.10) применимо только для коротких цилиндрических втулок с малой конусностью;
2) для цилиндра с прямоугольными пазами 122):
|
0 = n(D-h)hl-y-+iBH |
SID tgaptg(90-P)
' 2 tgctfl + tg(90-p)’ <2 I1>
где /, В, H — соответственно число, ширина и глубина пазов во внутренней поверхности материального цилиндра в зоне загрузки;
3) для цилиндра с прямоугольными коническими пазами:
0 = л(Я-/,)/,^-£ + я( D+lje + ZOT >v|lgад. (2.12)