Теория и практика экструзии полимеров
РАСЧЕТ ПРОИЗВОДИТЕЛЬНОСТИ ОДНОШНЕКОВОГО ЭКСТРУДЕРА ДЛЯ ПСЕВДОПЛАСТИЧНОЙ ЖИДКОСТИ
Экспериментально-теоретическими исследованиями экструзии псевдопластичной жидкости в одношнековом экструдере в разное время занимались авторы работ [5, 6, 35, 36|. Обобщение публикаций поданному вопросу наиболее полно изложено в монографии Р. В. Торнера |5). Ниже рассматривается разработанная М. М. Балашовым |35| теория одношнековой экструзии, наиболее простая, по нашему мнению, для инженерных расчетов.
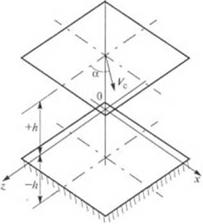
В указанной работе автором рассматривается плоская модель зоны дозирования одношнекового экструдера (рис. 2.33), в которой, как примято во всех известных работах [1—7], шнек (нижняя плоскость) неподвижен, а цилиндр (верхняя плоскость) движется относительно шнека со скоростью Vc. При этом начало неподвижной системы координат расположено в середине канала, ось дг на
правлена поперек винтовою канала, у — по высоте винтового катит, а ось z — вдоль винтового канала, причем ось oz перпендикулярна плоскости постоянного давления, т. е. плоскости xoz.
В предположении, что Р = P(z), vy = 0, v = v(y) и что жидкость несжимаема, смачивает стенки канала, процесс изотермический, а течение установившееся, имеем:
|
I dvx Уху~2~ду' Улг= 0; I 0v. |
|
3vr Л Чхх = ^ = 0; дх dv., Y =^ = 0- Yk dz ' |
|
(2.95) |
|
др. |
<*хх |
||
|
дх |
дх |
ду |
dz |
|
Не.-. |
ух |
дх уу |
& 1 + |
|
ду |
дх |
ду |
dz |
|
др |
дх^ |
bzz |
|
|
д Z |
дх |
а у |
dz |
|
Тогда уравнение движения в компонентах тензора напряжений принимает вид: |
|
(2.96) |
С учетом принятых предположений и уравнений (2.95) получим из формул (2.96):
|
|
|
(2.100) |
|
dу d Р clx. v dz dу Из уравнения (2.97) следует. |
что
Тду - Ci,
л из уравнения (2.98) т
|
Гис. 2.33. К расчету топы дозирования о шошнекового экструдера ятя псевдо - н истинной (степенной» жидкости |
S'*c -
Движение жидкости в элементарном слое толщиной Ду, параллельном плоскости дг0г(см. рис. 2.33), под действием касательных напряжений, определяемых уравнениями (2.99) и (2.100), эквивалентно (при Ау-> 0) движению под действием касательных напряжений т, приложенных к границам слоя, если
|
(2.101) |
* = V + *yz = С,/ + ^У К + С2 К,
глс /, К — единичные векторы, параллельные осям ох и oz соответственно.
Второй член правой части уравнения (2.101) представляет собой вектор касательного напряжения, определяемого изменением давления вдоль оси oz:
|
|
(2.102)
|
(2.103) |
Геометрическая же сумма двух других членов является векю - ром xf, касательного напряжения, определяемого скоростью перемещения подвижной пластины (см. рис. 2.33):
тс = С| / + С2 К.
|
(2.104) |
Направление тс совпадает с направлением движения пластины, что очевидно при dp/dz = 0, т. е. уравнение (2.101) можно представить в виде:
т = тр + тс.
Модуль х равен:
|
|
|
К
|
Для псевдопластичной жидкости с реологическим уравнением вида
• <*v к
II - — /1*ГЛ /Л lA/'V
(где а, к — реологические константы полимеров) из формулы (2.105) получим:
|
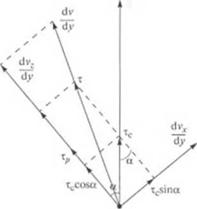
Рис. 2.34. Векторная диаграмма напряжений сдвига в зоне дозирования одношнеко - вого экструдера |
С учетом, что при простом сдвиге
|
(2.108) |
dv к-
dуяа"'
(где? р— единичный вектор суммарного касательного напряжения т), можно найти проекции производной вектора скорости на оси координат (рис. 2.34):
ft-l
dv. dv Тр + тс cosa /2 Л 2ГГ
—£--------------- = tf(tp + 2tpiccosa + Tc J х
dy dy т ' H ' '
(2.109)
x(tp + xc cosa);
|
dv; dv xc cosa dy dy I |
ft-1
i{x2p + 2ipTccosa + ic) 2 xcsina. (2.110)
Для получения уравнения производительности шнека одношнекового экструдера достаточно рассмотреть уравнение (2.109). После его преобразования получим:
d —
^-^/,//(K2+2ATcosa+*2) 2 (K + ATcosa), (2.111)
SHAPE * MERGEFORMAT

где X = * idem; У = —; т/,„ = —Л — напряжение сдвига у
т Ар Л d с
ни (при у Л), определяемое изменением давления вдоль оси *.
Интегрирование уравнения (2.111) дает распределение проекций скоростей частиц потока на плоскость уо?.
Ы
(K2+2mosa+A2)2 +С
|
_ a4ph |
|
V. = |
подвижной пласти
|
1 ft + l |
(2.112)
Постоянная интегрирования С определяется при граничных условиях
|
axLh v7=—32- * к + |
|
ft+l |
Тогда
/, _
(K2+2A'rcosa + A'2) 2 _(| -2ХсскX2) . (2 ||3)
Постоянная АТдолжна быть определена из граничных условий у = Л; V. = Vc cosa.
от* Л
|
Следовательно, |
|
(2.114) |
Ус cos а = — (-Ф, к +1
а в частном случае, когда Vc перпендикулярна плоскости yoz„ т. е. cos а = 0, из уравнения (2.114) получим:
|
(2.115) |
Ус =2(п*рНФт,
|
А-1 |
где
Окончательно получим следующее уравнение для расчета про - и зводитсл ьности:
I Worth2
Q= j tVv. My - F, (2.116)
гле | Ы Ы
(Y2 + 2 AfKcos a + AT2) 2 _ (l _2 Afcos a + X2) 2
|
d Y. |
-1
При cos a = 0 уравнение (2.116) принимает вид:
|
(2.117) |
|
где |
|
dK. |
|
. Г *+1 к+1 F„= /|(к2 + Х2)2 -(l + X2) 2 |
|
* + 1 *+i |
|
Q = |
Расчет интегралов Fи Fm в общем виде не представляется возможным, за исключением некоторых случаев, например при к = 1:
f = 4^ АГ cosa-lj; Fm=-%.
Поэтому для совместного решения уравнений (2.114) и (2.116) должны быть применены численные методы интегрирования с помощью компьютеров.