Теория и практика экструзии полимеров

ОСОБЕННОСТИ ПЛАВЛЕНИЯ СМЕСИ ГРАНУЛИРОВАННЫХ ПОЛИМЕРОВ С ДИСПЕРСНЫМ НАПОЛНИТЕЛЕМ ПРИ ПЕРЕРАБОТКЕ НА ОДНОШНЕНОВОМ ЭКСТРУДЕРЕ

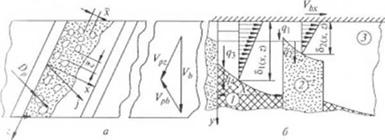
В случае переработки сухой смеси гранулированного полиме­ра и дисперсного наполнителя в зоне пластикации (сжатия) об­разуются характерные зоны уплотненного наполнителя, причем, в зависимости от плотности дисперсного наполнителя и его объемного содержания, наблюдается определенное соотношение между площадями контакта с поверхностью шнека и цилиндра полимера Sp и наполнителя S). Протяженность зон уплотненного наполнителя в направлении осей х и z (рис. 2.50, а) может оцени­ваться средним значением расстояний между гранулами полиме­ра х и z • Значения * и z > » зависимости от условий загрузки
компонентов и степени их предварительного смешения, могут ме­няться в широких пределах. В условиях тщательного смешения, югда x = z, принимая форму зоны полимера за цилиндр диамет­ром Dp и высотой, равной глубине винтового канала шнека, рас - » юяния х и Z можно выразить как 110, 41)

(2.221)

при (1-п/4)<С0у < I.

В случае полного отсутствия предварительного смешения s z =0.5И/. а зона уплотненного наполнителя может распола - I а гься как у толкающей, так и у пассивной стенки винтового кана - I I шнека.

Рассмотрим случай достаточно полного предварительного сме­шения полимера и наполнителя и пленочного механизма плавле­ния с расположением массы циркулирующего расплава вблизи пассивной стенки винтового канала шнека |45|.

На всех упомянутых ранее стадиях развития и протекания про­месса плавления необходимо проведение раздельного анализа из­менения толщины пленки над областью полимера 6(х, z) и над областью наполнителя S2(x, Z) вследствие различных механизмов протекания процессов (рис. 2.50, б).

На стадии распространения процесса плавления на всю шири­ну канала (индекс /), заканчивающейся при Z = IV/lga, для зоны полимера уравнение теплового баланса приобретает вид 110]:

Для этой сталии скорость роста толщины пленки полимера над зоной наполнителя (рис. 2.50) может быть принята равной

= ~r~ = const, (2.223)

dz Z ♦

где §2/ — толшина слоя полимера нал наполнителем; &2I =(l + 2)Df [411.

На последующих стадиях процесса плавления увеличение тол­щины слоя расплава над зоной наполнителя обусловлено уносом частице поверхности наполнителя под действием касательных на­пряжений в пленке расплава:

. И2 У

<2-224>

где pi - эффективная вязкость расплава полимера при скорости сдвига в пленке расплава у2; скорость движения пробки относительно матсри;ьтьного цилин­дра.

При интенсивности уноса Ny (тн.) частиц наполнителя диамет­ром D/, уплотненного до плотности р^, изменение толщины плен­ки расплава ву'-м направлении составит |10|:

Изменение толщины пленки над зоной полимера (см. рис. 2.50) может быть рассчитано с использованием изложенной ранее мето­дики при учете следующих особенностей:

1) плавление полимера обеспечивает увеличение толщины пле­нок как в зоне расплава, так и в зоне наполнителя;

2) наличие наполнителя вносит изменение в теплотой баланс зоны полимер;! вследствие различия в их теплофизических свойствах;

3) характерная длина отдельных зон плавления полимера огра­ничена величиной Df, вследствие чего развитие процесса плавле­ния необходимо рассматривать в пределах этого размера. При этом взаимным влиянием отдельных зон можно пренебречь. Ис­пользуя для описания распределения температуры в пленке рас­плава уравнения, приведенные в работе |45| (см. также раздел 2.6.2), проведем анализ тепловых потоков.

В зоне наполнителя 2 (рис. 2.50, б) тепловой поток </ь идущий от расплава 3 к границе раздела «расплав — наполнитель», равен |1()|:

(2-226>

где У. р — коэффициент теплопроводности расплава nai и мера; Г* и Г, — температу­ры цилиндра экструдера и плавления полимера соответственно; ц2 — "эффектив­ная вязкость расплава полимера в пленке толщиной Sj(.t. z)

Тепловой поток <72 от границы раздела в массу наполнителя со­ставляет:

дТ,

где X/- коэффициент теплопроводности наполнителя; Т/- температура наполни - геля (см. область 2, рис. 2.50, б).

Поскольку на границе раздела между пленкой расплава и на­полнителем не происходит фазового перехода и можно принять

ю разность тепловых потоков Дq = q — <72 можно считать распре­деленной на два потока. Один поток направлен в наполнитель (Д<7/), а другой вызывает дополнительный нагрев полимера (Д<7Р), причем

1-ZL

V)

Последнее уравнение позволяет определить изменение толщины пленки расплава над зоной полимера б|(х, z) при условии расчета 82(лг, z) ПО уравнению (2.225). a (d;) и (d7/d. v■>, - из

анализа теплопередачи от пробки материала к шнеку по* уравне­ниям теплопроводности для шнека 110].

В зависимости от соотношения 5|(х, г) и 62(х, z) (см. рис. 2.50) возможны разные варианты относительного расположения про­филей областей полимера и наполнителя, что создает различные условия для диспергирования наполнителя.