Теория и практика экструзии полимеров

НЕНЬЮТОНОВСКИЕ ЖИДКОСТИ

В этом разделе проводится классификация не ньютоновских жидкостей и рассматриваются различные эмпирические и теоре­тические уравнения, связывающие неньютоновскую вязкость г со скоростью сдвига (или с напряжением сдвига) в случае простого изотермического сдвига. Влияние температуры на г| рассматрива­ется в разделе 1.5.

К не ньютоновским жидкостям относятся жидкости, кривая те­чения которых не является линейной, г. е. вязкость неньютоновс­кой жидкости не остается постоянной при заданных температуре и давлении, а зависит от других факторов, таких, как скорость сдвига, конструктивные особенности аппаратуры, в которой нахо­дится жидкость, а также от «предыстории» жидкости.

Реальные жидкости с нелинейной кривой течения можно раз­бить на три обширные группы:

1) системы, для ко торых скорость сдвига в каждой точке представ­ляет некоторую функцию только напряжения сдвига в этой же точке;

2) более сложные системы, в которых связь между напряжени­ем и скоростью сдвига зависит от времени действия напряжения или «предыстории» жидкости;

3) системы, обладающие свойствами как твердого тела, так и жидкости и частично проявляющие упругое восстановление фор­мы после снятия напряжения (так называемые вязкоупругие жид­кости).

Системы первого типа, свойства которых не зависят от време­ни, могут быть описаны реологическим уравнением (1, 5—7)

Y = /W,

in которого следует, что скорость сдвига в каждой точке жидкости является функцией напряжения сдвига в той же точке. Такие ве­щества могут быть названы вязкими неиьютоиовскими жидкостя­ми. Их удобно подразделять на 3 группы - в зависимости от вида функции (1.23):

1) бингамовскис пластичные жидкости (бингамовскис пласти­ки);

2) псевдопластичные жидкости (псевдопластики);

3) дилатантные жидкости.

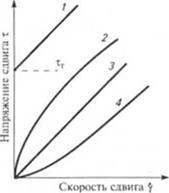
Кривые течения, характерные для этих трех типов жидкостей, приведены на рис. 1.4.

Бингамовский пластик. Кривая течения для этих материалов представляет прямую линию, пересекающую ось напряжения сдвига на расстоянии тт от ее начала. Напряжение текучести тт есть предел, превышение которого приводит к возникновению вязкого течения.

Реологическое уравнение для бингамовских пластиков (кото­рое Бингам вывел в 1916 г., а Ф. Н. Шведов — в 1889 г.) можно за­писать в виде:

/(т) = т-тт=П/>У’ т>тт;

/(т) = т-тт=0, т<тт,

i n - Пр - пластическая нязкость, или коэффи­циент жесткости при сдвиге, численно равный ынгенсу угла наклона кривой течения.

Объяснение поведения бингамов­ских пластиков исходит из предполо­жения о наличии у покоящейся жид­кости пространственной структуры, достаточно жесткой, чтобы сопротив - вггься любому напряжению, не пре­восходящему по величине тт.

Рис. 1.4. Кривые течения различных типов

■меткостей:

/ бингамовский пластик: 2 пссшопластич - П.1Ч жилкость; 3 - ньютоновская жидкость: 4 - ли - i. iполная жилкость

Если напряжение превышает тт, то структура полностью раз­рушается, и система ведет себя как обычная ньютоновская жид­кость при напряжениях сдвига т — тт. Когда же напряжение сдвига становится меньше хт, структура снова восстанавлива­ется.

Исевдопластики. Псевдопластичные жидкости не обнаружива­ют предела текучести, и кривая течения их показывает, что отно­шение напряжения сдвига к скорости сдвига, т. е. кажущаяся вяз­кость

постепенно понижается с ростом скорости сдвига. Кривая течения становится линейной только при очень больших скоростях сдвига. Предельный наклон, получивший название вязкости при беско­нечно большом сдвиге, обозначается через г„.

Кривые течения псевдопластиков в логарифмических коорди­натах в большинстве случаев оказываются прямыми с тангенсом угла наклона, отличным от I. Поэтому для описания жидкостей рассматриваемого типа применяют функциональную эмпиричес­кую зависимость в виде степенного закона:

т=тД (1.25)

где Iv — мера консистенции жидкости (чем выше вязкость жилкосги, тем больше т); п — характеризует степень исньютоновского поведения материала (чем боль­ше /г отличается от единицы, тем отчетливее проявляются его неныотоновекме свойства).

Здесь важно иметь в виду, что, хотя во многих случаях значе­ние п приблизительно постоянно в довольно широких пределах изменения скорости сдвига, для реальной жидкости это не имеем места, если рассматривать весь возможный диапазон напряже­ний сдвига. Отмеченное обстоятельство не создаст серьезных по­мех в инженерных приложениях, поскольку используемое на практике реологическое уравнение описывает жидкость в огра­ниченном диапазоне скорости сдвига, встречающемся в частных задачах. В этих пределах можно принимать значение п постоян­ным.

Часто встречается другая запись степенного закона:

Y(1.26)

В этом случае k > 1, а а тем больше, чем меньше вязкость.

Следует отметить, что размерности т и а зависят от показателя степени, но для многих инженерных расчетов это не имеет суще­ственного значения.

Кажущуюся вязкость г|ы для степенного закона можно выразить через п. Для этого в выражение для кажущейся вязкости подста­вим значение т из уравнения (1.25).

Гогла получим окончательно:

Лд =^- = тУл“1- (1.27)

н поскольку для псевлопластичсских материалов л < 1, то кажуща - '■II'я вязкость убываете возрастанием скорости сдвига.

Автор работы 121 высказывает предположение, что физическое I од кование нссвдонластичности. вероятно, заключается в том, что ■ возрастанием скорости сдвига асимметричные частицы или мо - в-кулы ориентируются. Молекулы вместо случайных (хаотичных) 1ВНЖСНИЙ, которые они совершают в покоящейся жидкости, сво­ими большими осями ориентируются вдоль направления потока. Кажущаяся вязкость будет убывать с ростом скорости сдвига до lex пор, пока сохраняется возможность дальнейшего ориентиро­вания частиц вдоль линии тока, а затем кривая течения становит­ся шнейной.

И степенном законе употребляются абсолютные величины, так >лк у (или I) могут быть и положительными, и отрицательными, но h должна быть всегда положительной. Заметим, что, когда ии - 1скс течения п равен I, степенной закон сводится к ньютоновско­му. Таким образом, увеличение отклонения п от единицы указы - гае г на неньютоновскую природу жидкости. Следует заметить, •по. согласно степенному закону, вязкость псевдопластичной мшкости становится бесконечно большой, когда у (или т) при - бнижается к нулю, а г стремится к нулю, когда у (или т) стано - вигся беспредельно малым. Для дилатантных систем справедливо • и'«ратное утверждение.

Общее соотношение — уравнение (1.7) — связывает напряжение м скорость сдвига для жидкости, подчиняющейся степенному за­кону, с учетом знака у •

. п

где знак т должен быть таким, как и знак у. Если у0 = 1 и т поло­жительно, то логарифмическое уравнение примет вид

lgT = lgT° +/ilgy,

показывая, что график зависимости lg т от Igy должен быть пря­мой линией для тех жидкостей, которые подчиняются степенному икону.

Оказывается, логарифмические кривые течения расплавов но - I нм еров часто являются прямыми линиями, если ограничиться одним-дву. мя порядками скоростей сдвига, но когда скорости ■ жига превышают несколько порядков, то они обычно отклоня-

27

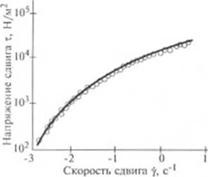
ются от прямой. Логарифми­ческая кривая течения для расплава полиэтилена (Ала­тон- 14 при 126 °С) показана на рис. 1.5. Она схожа с кри­выми для многих расплавов полимеров. При очень низ­ких скоростях сдвига кривая переходит в прямую, имею­щую тангенс угла наклона, равный единице, что указы­вает на ньютоновское пове­дение жидкости в этой обла­сти.

При скоростях сдвига 1

выше 0,01 с~‘ тангенс угла наклона кривой становится меньшим единицы, указывая на псевдопластическос поведение, причем с увеличением скорости сдвига он непрерывно уменьша­ется, тем самым увеличивая отклонение от поведения ньютоновс­кой жидкости.

Хотя ясно, что невозможно описать полную кривую, показан­ную на рис. 1.5, с помощью степенного закона, однако отдель­ные части кривой приближенно могут быть им описаны. Напри­мер, в области скоростей сдвига между 0,1 и 1,0 с-1 прямая ли­ния, на которую экспериментальные точки ложатся достаточно хорошо, имеет наклон около 0,59. Выбирая у0 равной 1 с-1, полу­чаем значение т°= 1,5- 105 дин/см2 (1,5- 104 Н/м2). Следователь­но, ti0 равна 1,5- 105 из (1,5- 104 11 - с/м2), а уравнение вязкости принимает вид

/г-1

1,510-

•0.41

и его можно использовать в пределах скоростей сдвига от 0,1 до 1,0 с-1 с ошибкой, составляющей менее 5 %.

Дилатантные жидкости. Дилатантные жидкости сходны с псевдопластиками тем, что в них также отсутствует предел текуче­сти, однако их кажущаяся вязкость повышается с возрастанием скорости сдвига.

Степенной закон и в этом случае часто оказывается пригод­ным, но показатели степени п уже превышают единицу, a k < 1.

В промышленной технологии дилатантные жидкости встреча­ются реже, чем пссвдопластики, но в случае применимости сте­пенного закона расчеты для материалов обоих типов становятся почти одинаковыми.