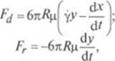Теория и практика экструзии полимеров

МОДЕЛЬ ДИСПЕРГИРОВАНИЯ АГЛОМЕРАТОВ ЧАСТИЦ НАПОЛНИТЕЛЯ

Процесс экструзии по своей природе неразрывно связан с про­цессами диспергирования и смешения.

В настоящее время экструдеры нашли широкое применение в качестве смссителей-пластикаторов непрерывного действия при производстве и переработке композиционных материалов, а также 1ля введения красителей или различных структурирующих доба­вок непосредственно в процессе переработки полимеров.

Введение наполнителей позволяет модифицировать физико­механические свойства и эксплуатационные характеристики и экономить исходное полимерное сырье.

Перспективным способом модифицирования свойств полиме­ров для получения материалов с заданными свойствами является введение дисперсных и армирующих (волокнистых) наполнителей. Структура и свойства наполненных полимеров как гетерогенных многокомпонентных систем в общем виде определяется двумя фак - горами. Первый заложен в самом принципе получения наполнен­ных материалов путем введения в полимеры наполнителей, раз­личных по физической и химической структуре, размеру и форме частиц и их содержанию в системе. Второй является результатом тех изменений в физико-механических свойствах и структуре по­лимерной матрицы, которые обусловлены взаимодействием на границе раздела «полимер — твердое тело».

Суммарное изменение свойств наполненной системы по срав­нению с исходным полимером происходит в результате одновре­менного действия обоих факторов. При этом в системе имеет мес­то определенное взаимодействие между частицами наполнителя и полимерной матрицей. Хотя до настоящего времени точно не ус­тановлено влияние химических или физических связей между по­лимером и наполнителем на свойства наполненной системы, можно считать, что для создания материала с оптимальными свойствами необходимо определить степень связывания полимера с поверхностью наполнителя. При этом большую роль играет сте­пень диспергирования частиц наполнителя в процессе экструзии, так как чем глубже протекает процесс диспергирования агломера­тов частиц наполнителя при экструзии, тем больше поверхность их контакта с полимерной матрицей. При этом следует отметить, что подавляющее большинство используемых в качестве вводи­мых в полимер ингредиентов обладает высокой степенью агрега­тирования исходных частиц. Присутствие в получаемой смеси агломератов приводит к образованию дефектов в структуре и анизотропии свойств изделия. Задачей диспергирования и после­дующего смешения является обеспечение таких однородностей распределения и дисперсности вводимых в полимер ингредиен­тов, которые обусловливают заданный комплекс свойств получае­мых материалов.

Сопоставительный анализ и практика работы смесительного оборудования показали, что одной из машин, обладающей высо­кой диспергирующей и смесительной эффективностью при полу­чении различных наполненных (композиционных) полимерных материалов на основе термопластичных полимерных материалов, является экструдер. Кроме того, экструдеры сочетают в себе про­цесс диспергирующего смешения с процессом непрерывного по­лучения профильных изделий.

Получение композиционных материалов с заданными физико - механическими свойствами предусматривает создание условий для равномерного распределения хорошо диспергированного на­полнителя. И то же время в процессах получения композитов с порошкообразным наполнителем при его введении в зону заг­рузки одношнскового экструдера наблюдается интенсивное об­разование агломератов порошкообразного наполнителя в зоне уплотнения и плавления полимера, которые подвергаются вдаль нейшем разрушению в последующих функциональных зонах экст рудсра 110). Размеры и прочностные характеристики образующих­ся агломератов (для данного типа наполнителя) определяются его компрессионными свойствами, содержанием наполнителя, разме­рами и формой частиц полимера, а также величиной давления, развивающегося в зонах загрузки и плавления экструдера. В то же время в большинстве конструкций одношнековых экструдеров интенсивное диспергирование частиц наполнителя осуществляет­ся вследствие создания высоких напряжений сдвига в расплаве пс - |крабатываемого материала. При этом диспергирование агломера­та порошкообразных наполнителей происходит путем отрыва от­зольных частиц наполнителя (или агломератов) под действием касательных напряжений. Интенсивность процесса диспергирова­ния агломератов определяется величиной сил связи частиц в них, шаченнем действующих касательных напряжений на их поверх­ности, а также скоростью отвода диспергированных частиц от по­верхности агломерата. Сама интенсивность процесса диспергиро­вания может быть охарактеризована количеством частиц диспер­гированного наполнителя, находящихся вблизи поверхности агломерата.

Механизм образования и разрушения агломератов впервые ис - i ic до вал Мак-Келви |4). Он рассматривает гетерогенную систему, и которой диспергируемая фаза находится в виде агрегатов, состо­ящих из двух частиц, а дисперсионная среда представляет собой вязкую жидкость. При этом предполагается, что агрегаты лиспер - шруемой фазы не взаимодействуют друг с другом, поскольку их концентрация в системе незначительна. В данной системе в про­цессе переработки (смешения) действуют когезионные силы, удерживающие частицы агломерата от разъединения, и поверхно­стные силы, возникающие при движении частиц относительно жидкости.

В приводимой работе применена подвижная система коорди­нат (рис. 2.38), начало которой находится в центре одной из час­ти агломерата. В результате анализа определяется положение центра другой частицы агломерата (в координатах х—у) на различ­ных стадиях процесса смешения.

При радиусе частицы R наименьшее расстояние между центра­ми частиц равно 2R, и его можно вычислить по формуле:

r=Jx2+y1. (2.173)

Предполагается, что в области 2R < г < г* сила притяжения, удерживающая частицы вместе, постоянна, а в области г > г* эта ила пренебрежимо мала. Критический радиус разделения г* представляет собой важный параметр всех процессов дисперги­рования и определяется природой сил, вызывающих агломера­цию.

Рис. 2.38. Мечами <ч оораiohummh и разрушения агломератов

Из рис. 2.38 видно, что при выбранной системе координат на окружающую частицы жидкую среду действует одноосная дефор­мация сдвига, вызывающая течение среды вправо со скоростью

V = yy.

Если рассматриваемые частицы имеют форму шара и число Рейнольдса при движении частиц относительно жидкости невели­ко, то увлекающая сила, действующая на частицу, определяется по закону Стокса как 6я/?цг*. Равнодействующую всех сил взаимодей­ствия между поверхностью сферы и окружающей жидкостью мож­но разложить на составляющие Fj и Fn которые определяются сле­дующими равенствами:

(2.174)

(2.175)

где cLt/d/ — скорость движения частицы в направлении оси х; iiy/iit — скорость движения частицы в направлении оси у, ц — виткость жидкости.

Пренебрегая силами инерции (что вполне допустимо для сис­темы, состоящей из очень маленьких частиц в жидкости с высо­кой вязкостью), получим:

Fd = FacosO; Fr = FasnO,

где 0 — угол, образованный прямой, проходящей через начало координат и центр частицы (см. рис. 2.38); F0 — сила взаимодействия между частицами.

Из совместного решения уравнений (2.174), (2.175) и (2.176) с учетом, что cos 0 = x/r, a sin 0 = у/г, автором работы [41 получена с юдуюшая система обыкновенных дифференциальных уравне­ний:

dx

=УГ_.

d/ г

чс I — независимая переменная (время); х, у — зависимые переменные. Из уравнений (2.177) и (2.178) получим:

dу у

I ле

r бяАуц 4 л Ах

л г—I

г напряжение сдвига, возникающее в жидкости.

Для частиц малых размеров можно принять, что г~х + у. Тогда уравнение (2.179) принимает вид

dx

^+хК-^-Ку,

л решение его выглядит как

(2.182)

I ic С постоянная интегрирования.

Постоянная интегрирования С находится из условия, что в на­чальном положении за координаты центра тяжести приняты (xq, у0). Тогда уравнение (2.182) принимает вид:

х + У У0_,

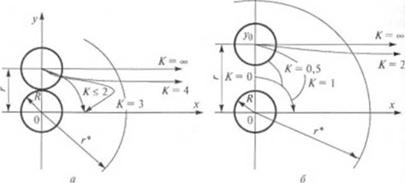
Из последнего уравнения видно, что траектория (а следова­тельно. и течение процесса диспергирования) определяется пара­метром А, критическим радиусом г* и первоначальной ориентаци­ей агрегата (рис. 2.39).

Рассмотрим агломерат из двух частиц, ориентированный, как показано на рис. 2.39, я, где

А =0,5; лг0=0;

/■• = 3; >’о = 1.

При этом на жидкую среду действует деформация сдвига, вы­зывающая одноосное движение среды вправо.

Если сила притяжения частиц h'a мала или в жидкости возника­ют значительные напряжения сдвига, то величина К становится очень большой |с. м. уравнение (2.180)j. В предельном случае, ког­да К-ь «*>, движение частиц совпадает с линиями тока жидкой сре­ды, что свидетельствует о том, что диспергирующее смешение сводится к простому смешению (см. рис. 2.39, а). В области, где г > г*, величины Fa = 0 и К =* », и в данной области все пути дви­жения частиц совпадают с линиями тока. Влияние силы взаимо­действия частиц становится заметным, когда К является конеч­ным числом. Например, если К — 4, агломерат сперва слегка пово­рачивается, а затем верхняя частица (см. рис. 2.39, а) движется вправо и вниз по искривленному пути до тех пор, пока не достига­ется значение критического радиуса, когда силы взаимодействия между частицами Уа становятся равными нулю, после чего верхняя частица движется по линии тока вправо.

Тот же самый процесс начинается в случае, когда К = 3, но в конце концов частица достигает того положения, когда, вслед­ствие уменьшения увлекающей силы жидкости, баланс сил стано­вится неблагоприятным, после чего направление движения изме­няется и частица снова объединяется с прежней частицей.

При К = 2 силы взаимодействия намного превышают вязкост­ные силы и поэтому расстояние между центрами частиц не будет изменяться. Центр верхней частицы пройдет четверть окружности (см. рис. 2.39, а), в результате чего агломерат повернется так, что прямая, проходящая через центры обеих частиц, совпадет с лини­ей тока. Следовательно, в условиях данного примера разрушение агломерата произойдет только в том случае, когда параметр К> 4

|уравнсние (2.180)|. При более благоприятной первоначальной ориентации для осуществления диспергирования достаточно меньшее значение параметра К. Например, если первоначаль­ная ориентация частиц соответствует случаю, показанному на рис. 2.39, б, диспергирование может произойти далее при К = 2.

Из приведенного анализа можно сделать следующие выводы:

1) высокие напряжения способствуют диспергированию; суще­ствует некоторое значение напряжения сдвига, ниже которого во­обще не происходит диспергирования;

2) в случае, если напряжение сдвига немного превышает кри­тическое значение, то будут подвергаться разрушению только аг- юмераты с благоприятной первоначальной ориентацией (боль­шая ось которых перпендикулярна линиям тока). Следовательно, в смесителях, где осуществляется только одномерное движение перерабатываемого материала, произойдет разрушение лишь тех агломератов, первоначальное положение которых благоприятное. Однако, если в смесителе осуществляется непрерывное изменение направления потока, то в дальнейшем также будет происходить шепергирование агломератов. В конце концов, через определен­ный промежуток времени под воздействием напряжений сдвига каждый агломерат примет благоприятное положение и будет раз­рушен;

3) если предположить, что сила взаимодействия частиц F0 от­носительно независима от размера частиц, то из уравнения (2.180) видно, что параметр К прямо пропорционален радиусу R. т. е. аг - юмераты, состоящие из больших по размеру частиц, легче разру­шаются по сравнению с агломератами, состоящими из частиц меньших размеров.

Работа Мак-Кслвн |4| представляет собой идеализированный случай образования и разрушения агломератов, так как в реальных процессах экструзии наполненных полимеров будет наблюдаться несколько иная картина образования и разрушения агломератов. )го объясняется тем, что к расплавам полимеров вряд ли приме­ним закон Стокса. Кроме того, частицы наполнителя редко имеют форму с<|>срм, за исключением тех случаев, когда в полимер до­бавляются стеклянные микросфсры.