ТЕОРИЯ ГОРЕНИЯ И ТОПОЧНЫЕ УСТРОЙСТВА

РАСПЫЛЕНИЕ ЖИДКИХ ТОПЛИВ

Использование центробежного эффекта в механических и вращаю­щихся форсунках (см. § 11-1, рис. 11-1 и 11-8) приводит к разрыву ■сплошного потока. Жидкость внутри выходного канала форсунки при­нимает форму полого цилиндра, заполненного парами и газами. Из сопла вытекает эмульсия, образуя жидкую пленку в виде раскрываю­щегося гиперболоида. В направлении движения сечение гиперболоида увеличивается, а пленка жидкости утоньшается, начинает пульсировать и, наконец, распадается на быстродвижущиеся капельки, которые в по­токе подвергаются дальнейшему измельчению.

В паровых форсунках (см. § 11-1, рис. 11-7) первичное дробление производится за счет кинетической энергии пара, истекающего из сопла форсунки. Капли первичного дробления приобретают скорость паровой струи, обычно соответствующую критической скорости.

Движущаяся капля подвергается давлению газовой среды. Среда стремится расплющить и раздробить каплю. Давление среды на дви­жущуюся в ней каплю определяется силой трения среды Р на лобовое

Сечение капли Т7:

/>> = •£• (Ю-14)

Пренебрегая силой тяжести и рассматривая лишь действие среды, получаем, что сила трения:

Р=‘фЯрГ2. (10-15)

В формуле:

■ф — коэффициент сопротивления среды;

Р — плотность среды;

№ — относительная скорость капли по отношению к окружающей среде.

Тогда давление на единицу лобового сечения капли

Р1 = 'ФР^2. (10-16)

Поверхностное натяжение придает частице сферическую форму и тем самым сохраняет ее. Давление, испытываемое шаровой каплей под действием поверхностного натяжения, составляет:

Р,= Ц-. (Ю-17)

В формуле:

О — коэффициент поверхностного натяжения жидкости, Н/м;

Г—радиус капли, м.

Дробление капли жидкого топлива на более мелкие происходит тогда, когда рС>р2, а максимальный размер капли получается при условии:

/?1 = /?2 (10-18)

И составляет:

Г = ФрГг* (10-19)

Согласно данным ВТИ при обычно применяющемся нагреве мазу­та до 80—90° можно принять коэффициент поверхностного натяжения а = 0,03 Н/м. Коэффициент сопротивления г|) зависит от числа Рейнольд­са и в пределах Не = 103—105 составляет 0,2.

Подставляя численные значения а и г|) в формулу (10-19), получа­ем, что максимальный радиус капли г, мм,

(Ю-20)

Из формулы (10-19) следует, что тонкость распыления зависит от

Величины поверхностного натяжения, плотности среды и скорости. Так

Как для нефтепродуктов поверхностное натяжение уменьшается с воз­растанием температуры, то тонкость распыления при этом возрастает. Тонкость распыления значительно увеличивается и с возрастанием ско­рости.

Обобщением результатов экспериментальных исследований мето­дом теории подобия была получена следующая функциональная зави­симость для среднего размера капель жидкости при воздушном и паро­вом распылении [Л. 31]:

4=/(-?£>: йг£)- (1°-21)

В формуле:

Й — средний диаметр капель, мм;

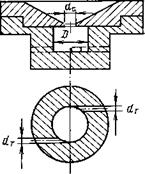
И — характерный геометрический размер форсунки (см. на рис«

10- 3), мм;

[х — коэффициент вязкости жидкости, Н-с/м2; рж — плотность жидкости, кг/м3;

<у — коэффициент поверхностного натяжения, Н/м; рг — плотность газа, кг/м3;

№ — относительная скорость между воздухом и жидкостью, м/с. Критерий ц,2/рж(т/) характеризует соотношение сил вязкости*, инерционных сил и поверхностного натяжения, а критерий р^Ю/а— отношение инерционных сил воздушного пото­ка к силам поверхностного натяжения.

При малых значениях сил вязкости жид­кости по сравнению с инерционными силами и силами поверхностного натяжения первым критерием можно пренебречь, тогда зависи­мость (10-21) упрощается и принимает вид:

Л _ г /

Обработкой опытных данных по зависимо­сти (10-22) получено, что с увеличением вели­чины критерия рг№2£>/а относительный размер капли к/И уменьшается. Это означает, что рас­пыление улучшается с увеличением скорости истечения распыливающей среды, плотности газовой среды и с уменьшением поверхностно­го натяжения жидкости.

При распылении жидкости центробежны­ми механическими форсунками была получена в [Л. 32] зависимость для среднего размера капель в следующем виде:

ЙГ = Л°>бГ1о,1Нео>7 ' (Ю-23)

В формуле:

^ —средний массовый диаметр капель распыленной жидкости;

Йс — диаметр сопла форсунки;

К — константа; ф-Аг) <Ъ

А = -—------------- геометрическая характеристика форсунки, размеры

Которой обозначены на чертеже (рис. 10-3), характеризующая отноше­ние окружной составляющей скорости жидкости к осевой; п — число подводящих каналов форсунки;

— -^-г и Яе = р-^^

РжООс Ц-

Из соотношения (10-23) следует, что при механических форсун­ках распыление улучшается с уменьшением вязкости, коэффициента поверхностного натяжения, диаметра сопла и увеличением относитель­ной скорости потока.

Влияние двух последних факторов выражается законом:

(10-24>

Учет разобранных выше закономерностей позволяет рационально организовать распыление жидкого топлива перед его сжиганием.