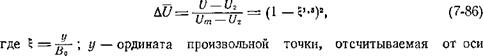ТЕОРИЯ ГОРЕНИЯ И ТОПОЧНЫЕ УСТРОЙСТВА

НАРАСТАНИЕ РАСХОДА ЖИДКОСТИ ПО ДЛИНЕ СТРУИ

В результате увлечения газа из окружающей среды масса струи увеличивается. В плоской изотермической струе с равномерным выход­ным полем скорости на начальном участке расход газа через произ­вольное сечение составляет:

Ух

В — 2р{У0 (Ь0 — г/1) 4“ 2р | и йу. (7-55)

У2

Из уравнения (7-1)

^=гу0[1-Ял)]+ОД(л). (7-56)

Имея при этом в виду, что согласно определению Т)

У— у 2

Йу=Ъйц и что при изменении у от г/1 до г/2 л изменяется от 0 до 1, вычислим интеграл в правой части уравнения (7-56):

TOC o "1-5" h z Ух 1

Udy = Ь^{U.l-f(1{^ + U, f (11)} а-ц = Ь(0,55(7, + 0.45У,). (7-57)

У* б

В нем величины интегралов составляют:

1 1

^ {(1|) Ж] = 0,45, у [ 1 _ I (,()] А, = 0,55. (7-58)

0 0

Подстановка.(7-57) в уравнение (7-55 )с учетом (7-58) дает:

С = 2р{У0(60—У*) +2рЬи0 (0,55+0,45т), (7-59)

Где т={У2/{У0.

110

На начальном участке струи расход газа в долях от начального расхода Go — 2U0b0з) увеличивается на:

-гг=£ - 1='1 (°’55+°’45т - т)- <7-60)

Где Ъ=Ь1Ь0.

Учитывая соотношение для у^Ь согласно (7-23) и соотношение для ширины струи по (7-11) и (7-20), получаем:

-^ = C3i^(0,134 + 0,316m)*. (7-61)

В случае затопленной плоской струи, для которой т—0 и С3=0,27,

= 0,03623с. (7-62)

С/о

Расход жидкости на основном участке плоской изотермической

Струи с равномерным выходным полем скорости можно подсчитать как

О

G = 2з>^Udy. (7-63)

Уг

Из уравнения (7-2)

U~Um№+Vz[l-f(l)]. (7-64)

Подставив выражение,(7-64) в уравнение (7-63) и проинтегрировав его с учетом того, что

Jf®dt = 0,45, a j[l —/(?)] <Й = 0,55,

0 0

Получим величину расхода в основном сечении струи. Отнеся его к рас­ходу в начальном сечении, получим величину относительного расхода

На основном участке плоской струи

Я - = Ь{ 0,45 Ьm + 0,55m), (7-65)

О о

Где

Ь = Ь/Ь.; Um = UmlU0.

В случае плоской затопленной струи, для_которой С3=0,27, т=О и xжO, с учетом закономерностей, (7-50) для Um и (7-12) для ширины пограничного слоя:

0,375 Ух, (7-66)

А относительное нарастание расхода составляет:

LG

0,375 Ух - 1. (7-67)

(?о

Аналогично рассчитывается относительный расход в основном уча­стке осесимметричной струи, который для затопленной струи (/72 = 0, х&0, С—0,22) составляет:

Я - = 0,155л:. (7-68)

Из сравнения выражений (7-66) и (7-68) следует, что осесиммет­ричная струя эжектирует интенсивнее, чем плоская.

Если температура струи отличается от температуры окружающей среды, то она называется неизотермической. При турбулентном расширении неизотермической струи увлечение в нее окружающего га­за, обладающего иной температурой, приводит к теплообмену между струей и окружающей средой. Если температура струи ниже темпера­туры среды, то истечение струи сопровождается ее нагревом; напротив, если температура струи выше температуры окружающей среды, — охлаждением.

На начальном участке, в ядре постоянных скоростей, температура остается неизменной и равной температуре газа на выходе из сопла. В турбулентном пограничном слое происходит интенсивный теплообмен. По мере увлечения окружающего газа в поперечных сечениях струи избыточные температуры, представляющие собой разность между тем­пературой в данной точке струи и в окружающей среде, убывают от максимального значения до нуля. На основном участке кривые избы­точных температур имеют максимум на оси. Дальнейшее разбавление струи окружающим газом приводит к все большему выравниванию тем­пературы струи с температурой окружающей среды, поэтому избыточ­ные температуры падают также по мере удаления от сопла.

В зоне смешения неизотермичесиой струи под влиянием изменения температуры изменяется плотность газа, т. е. в данном случае имеется струя сжимаемого газа. Полагая, что механизм турбулентного расши­рения неизотермической струи является таким же, как и изотермиче­ской струи, соотношение для интенсивности расширения газовой струи в зависимости от параметров потока на границах зоны смешения, на­зываемое уравнением распространения струи, можно выразить соот­ношением (7-7) при подстановке в него выражения для градиента скорости

DU _ Ut—Ut (7-69)

Dy b

И характерного значения средней скорости в зоне смешения, взятого с учетом различия плотностей смешивающихся газов

Ё/= (7.70)

Pi + Рг

Подстановка (7-69) в (7-70) после некоторых преобразований дает:

I»=c8!+^-!=2-. (7-71>

Dx 2 1 рщ

Таким образом, угловой коэффициент расширения неизотермиче­ской струи

С„ = С, ‘ + 1* • (7-72>

1 1 + р т

На начальном участке параметр сжимаемости Р=_^" и безразмерна» скорость т = а на основном участке р = ps/pm, m — U2fUm. Числен-

U %

Ное значение постоянной С3 в формуле (7-72) такое же, как на начальном1 участке изотермической (р=1) затопленной струи (т = 0).

При значениях 0,4 в диапазоне 0,3^р^1,4 расчетные данные Сн по (7-72) удовлетворительно совпадают с опытными, которые при

112

Дальнейшем увеличении т практически не изменяются. Это объясня­ется преобладанием влияния начальной турбулентности потока, кото­рая не учтена при выводе формулы (7-71), над влиянием турбулент­ности, генерируемой в зоне смешения.

Так как давление в струе и в окружающей среде одинаково, то параметр сжимаемости может быть представлен как

-й-=-р - = 0.

Р1 Тг

Тогда формула (7-72) может быть представлена в виде

С«=С»Ф1Т^- <7-73>

Где вц я С3 — угловой коэффициент неизотермической и изотермической затопленной струи.

На основном участке на значительных расстояниях от сопла угло­вой. коэффициент нарастания ширины изотермических и иеизотермиче- ских струй практически одинаков и равняется С=0,22.

Экспериментальные исследования, проведенные как с затопленны­ми, так и со спутными неизотермическими струями при отношении на­чальной температуры струи к температуре окружающей среды 0 = = 7УГв=0,32-г-1,43 и т=0+0,6, показывают, что профиль безразмер­ной скорости в поперечных сечениях универсален. ,

На начальном участке профиль скорости удовлетворительно опи­сывается уравнением (7-1), а на основном — уравнением (7-2).

Опыты показывают, что в безразмерных координатах кривые из­быточных температур в различных сечениях начального участка струи1 сливаются в одну универсальную кривую:

ДТ=^-=т^ = 1-^. <7-74>

А на основном участке поле безразмерных избыточных температур опи­сывается уравнением:

Д?=ЖГ=&=1-^ (7-75>

В уравнении:

&Т=Т—Гг — избыточная температура в данной точке;

ДГо^Го—Тг — начальная избыточная температура; ,

АТт=Тт—Тг — избыточная температура на оси струи;

Тт — температура на оси струи в данном сечении;

То — температура газа на выходе из сопла;

Т2 — температура в окружающей среде;

Т — текущая температура в пограничном слое струи.

Следовательно, поля избыточных температур во всех сечениях как начального, так и основного участка струи подобны. Это означает, что в сходственных точках различных сечений струи безразмерные величи­ны избыточных температур одинаковы и не зависят от скорости исте­чения.

Из подобия полей избыточных температур следует, что изотермы безразмерных температур в основном участке являются прямолинейны­ми лучами, сходящимися в полюсе струи, а в пограничном слое началь­ного участка — прямолинейными лучами, сходящимися на выходной кромке сопла.

8— 541 113-

Так как явления турбулентной диффузии, теплопередачи и переда­чи количества движения совершаются благодаря одному и тому же внутреннему механизму дереноса вихрей, то между изменениями скоро­стей и температур должна существовать определенная закономерность.

Из сравнения формул (7-2) и (7-75) следует, что

(7-76)

Т. е. безразмерная избыточная температура в любой точке поперечного сечения в основном участке плоскопараллельной, а также и осесиммет­ричной затопленной струи равна корню квадратному из безразмерной скорости в этой же точке. Последнее означает, что теплопередача при свободной турбулентности интенсивнее переноса импульсов и поэтому температуры выравниваются быстрее, чем скорости.

Такой вывод был получен в теории свободной турбулентности Тей­лора, а по гипотезе свободной турбулентности Прандтля безразмерные профили избыточной температуры и скорости в затопленной струе по­лучаются одинаковыми. Теория Тейлора дает лучшее совпадение с опытом.

При истечении струи с начальной температурой Го в нагретую сре­ду Т2>Т0 удобно зависимости (7-74) и (7-75) представлять в следую­щем виде:

АТ Т2 — Т

TOC o "1-5" h z АТ0 Тг — То 71

И

3

АТ Т—Тщ _____________ р2

А 'Г ------------ —-¥■ 'Г ’

АТт Тч — Тщ

Закон распределения температуры вдоль оси в основном участке струи можно получить, используя постоянство энтальпии струи во всех ее поперечных сечениях. Если энтальпию струи определять по избыточным температурам, т. е. принимать за нуль температуру окру­жающей среды, то избыточная энтальпия увлекаемого в струю газа будет равняться нулю, а избыточная энтальпия всего газа, протекаю­щего через любое сечение струи, будет величиной постоянной и равной избыточной энтальпии газов, вытекающих из сопла за равный промежу­ток времени. Увлечение в струю окружающего газа и увеличение массы газов в струе в силу постоянства избыточной энтальпии будут сопро­вождаться падением избыточных температур.

Закон падения избыточных температур должен быть аналогичным закону падения скорости, так как и падение температур и падение скорости пропорционально притоку окружающего газа в струю.

Г. Н. Абрамовичем получено соотношение между безразмерными избыточными значениями температуры и скорости на оси основного участка струи в виде

ЙЛ'т = к1Шт.

Для затопленной плоской струи с равномерными начальными по­лями скорости и температуры &3.т = 0,86, а для осесимметричной &з. т = 0,75.

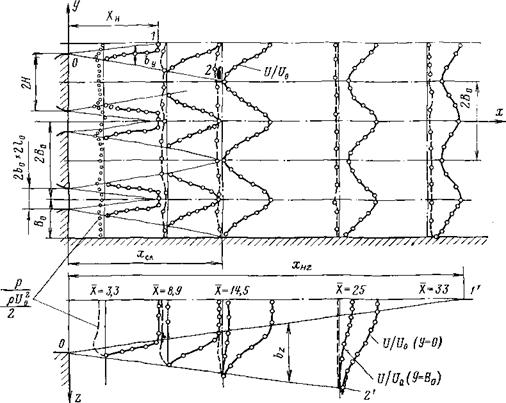
При организации сжигания топлив, в камерных топках применяется система плоских и осесимметричных струй, распростра­няющихся в топочном пространстве. В качестве примера рассмотрим систему плоских параллельных струй, вытекающих из плоских сопл, расположенных, в один ряд параллельно друг другу большими ося]МИ выходных сечений и ограниченную двумя плоскостями, перпендикуляр­ными плоскости среза сопл и параллельными их большим граням.

Струи рассматриваемой системы в своем движении ограничены боковыми стенами. Расстояние от стен до оси ближайших к ним сопл Во равно половине расстояния 2В0 между осями сопл, ширина сопл — 2Ь0, высота 2/0 (рис. 7-3).

Аэродинамика системы плоских параллельных струй была иссле­дована экспериментально [Л. 17] в изотермических условиях при из­менении геометрических параметров сопл и системы в пределах:

'ч В0

Относительный шаг между соплами В0 = - г— = Зч - 15;

О0

Относительная высота сопл /0 = /„/&, = 2,5 -4- 10;

Полуширина сопла Ьд = 5,5; 7,5; 10 и 12 мм;

Скорости истечения из сопл 15 - г - 50 м/с.

На рис. 7-3 для иллюстрации приведены поля скоростей и стати­ческого давления для системы с Во = В0/Ь0 —3,67 1о = 1о/Ьй=4,5 и Ь0 = = 12 мм в различных поперечных сечениях в плоскости ху при г — = 0 и в плоскостях хг при у — 0 и у = В0.

По выходе из сопл каждая из струй развивается самостоятельно. По мере удаления от сопл струи увлекают газ из окружающей среды, расширяются и на некотором расстоянии хсл от обреза сливаются в единый поток.

В зависимости от шага между соплами возможны три положения точки слияния:

Первое, когда слияние струй происходит за начальным сечением,

-Я'СЛ

Второе — на длине, равной длине начального участка хСл=хп;

Третье — на длине, меньшей, чем протяженность начального участ­ка Хсп^Хн-

На рис. 7-3 приведен и далее рассмотрен как более общий первый случай.

В системе плоских струй можно выделить две характерные зоны течения: раздельного и совместного движения струй.

В зоне раздельного движения в результате взаимодействия струй с окружающей газовой средой в плоскостях ху и хг образуются струй­ные пограничные слои Ьу и Ьг. В межструйном пространстве продоль­ная составляющая скорости равна нулю. По мере удаления от сопла пограничные слои расширяются, а ядро потенциального течения в пло­скости ху при 2 = 0 и область двумерного течения, характеризующиеся соответственно постоянством начальных параметров истечения и нали­чием зоны, где ди/дг = 0, уменьшаются, деформируясь в точки соответ­ственно на расстояниях х—хи и х — х1и. На внутренней границе 0—1 пограничного слоя Ьт и=и0, а на внешней границе 0—2 11=0. В пло­скости хг внутренняя граница пограничного слоя обозначена линией 0—Г, а внешняя—0—2'.

Течение в системе плоских параллельных струй является трехмер­ным. Однако наиболее характерной и определяющей является струк­тура течения в плоскости ху, проходящей через малые оси сечения сопл. В этой плоскости на участке от начального сечения до сечения х—хт задачу можно рассматривать как двумерную.

В зоне раздельного движения струй статическое давление в попе­речных сечениях практически постоянно и одинаково на всей ее длине.

Величина разрежения в межструйном пространстве зависит от гео­метрических размеров сопл и расстояния между ними 2Н, влияние которых характеризуется величиной критерия # = #//0, показывающего отношение начального межструйного расстояния к высоте сопла. Чем меньше Н, тем разрежение больше.

Поля скоростей в пограничном слое начального участка каждой струи системы и в ее основном участке подобны и описываются уравне­ниями (7-1) и (7-2), в которых следует принять [/2—0.

Как показали опыты, ширина зоны смешения как в начальном, так и в основном участке струй нарастает с удалением от сопла по линей­ному закону:

Ь —— Ссист^» (7-78)

Отсчет х производится для начального участка от полюса зоны смешения, а для основного участка—от полюса струи.

Величина углового коэффициента расширения зоны смешения 'Ссист зависит от простенка между соплами 2Н и их высоты 2/о. С уве­личением 2/0 и уменьшением 2Н ширина зоны смешения нарастает бо­лее интенсивно, коэффициент Ссист увеличивается. Опытные значения безразмерного относительного углового коэффициента Ссист^Ссист/Сз в зависимости от параметра Н в диапазоне его значений # = 0,3—1,2 могут быть аппроксимированы линейным законом для начального уча­стка х<.хп

ГНс«„=1.24-0,2Я, (7-79)

А для основного {х>хи)

Сосн. сист = 1,36 — 0,3 Н, (7-80)

Причем при II ^ 1 ,2, Ссист— 1«

Уменьшение параметра Н до значений 0,15—0,2 и менее приводит к качественному изменению картины течения системы струй. В этом ■случае разрежение, создаваемое в межструйном пространстве, оказы­вается недостаточным для удовлетворения эжекционной потребности системы струй только за счет подсоса газа из окружающей среды.

В межструйном пространстве в центральной части струй возникают об­ратные циркуляционные токи, удовлетворяющие эжекционные потреб­ности этой части струи.

В связи с большим угловым коэффициентом расширения зоны сме­шения в струе, находящейся в системе струй, начальный участок коро­че по сравнению со свободной струей. Например, это различие между длиной начального участка для системы струй с параметрами.6 = 3,5 »и /о=Ю составляет 1,ЬЬ0 при длине (9-М0)60 начального участка за­топленной струи, вытекающей из тех же сопл, т. е. примерно 20%-

На основании результатов опытов были определены расход жидко­сти и количество движения в различных сечениях струи в системе на единицу высоты сопла.

Чем меньше Н, тем интенсивнее массообмен с окружающей средой и тем больше отличие эжекционных способностей струи в системе от эжекционной способности свободной струи.

Относительный избыточный расход, характеризующий эжекцион­ные способности системы струй в начальном участке (х=хп), возраста­ет по линейному закону

Ад == 0,0362СнаЧ. ист^, (7-81)

А на основном участке (*сл>*>*н) по параболическому

Дё = 0,375 уЪ

ОСК. СИСТ-^ 1, (7-82)

Оставаясь после слияния струй до хш постоянным.

В сечении, где происходит слияние струй, расход не зависит от Л

0 = £= 1+0,8 У п, иВ. (7-83)

И соответствует расходу в свободной струе в сечении, в котором шири­на пограничного слоя равна Во.

Используя соотношение (7-78) и имея в виду, что после слияния струй, ширина пограничного слоя Ь = В0, можно определить длину уча-

117

Стка раздельного движения струй, т. е. длину участка от обреза сопл до сечения, в котором происходит слияние струй

Хсл = тЗ---------------------------------------------------- (7-84)

<->ссн. сист

Количество движения в системе струй в полосе В о как в зоне раз­дельного, так и в зоне совместного движения, в пределах двумерного течения в плоскости ху при 2=0, вдоль оси потока сохраняется посто­янным:

(7-85)

Аналогичные результаты дали подсчеты величины импульса и по всему сечению, занятому потоком, т. е. вдоль по течению. импульс со­храняется постоянным.

Изменение осевой скорости в струях системы удовлетворительно описывается уравнением (7-53) для изменения скорости в свободной струе при значении коэффициента С для этих струй. С уменьшением величины параметра Н вследствие возрастания коэффициента С длина начального участка сокращается, струя расширяется интенсивнее, осе­вая скорость на основном участке до слияния струй падает быстрее.

Исходя из наличия подобия скоростных и температурных полей и постоянства давления, можно для расчета начального и основного участков в зоне раздельного движения струй пользоваться методом рас­чета затопленной струи, принимая при этом значение единственного эмпирического коэффициента С согласно данным для системы струй по

(7-79) и (7-80).

После слияния струй в единый поток, т. е. в зоне совместного дви­жения, эжектирование газа из окружающей среды по большим граням прекращается и расход в плоскости ху при 2=0 сохраняется постоян­ным до сечения х=хш. Струи начинают взаимодействовать друг с дру­гом. В сечениях, лежащих вниз по потоку от места слияния, профили скорости имеют максимумы на осях струй, практически совпадающих с осями сопл. Между каждой парой максимумов лежат минимальные значения С/г скорости. С увеличением расстояния от сопла осевая ско­рость ит падает, а скорость С/2 возрастает, т. е. происходит выравнива­ние кинематической неравномерности потока.

Учитывая симметрию потока, его можно разбить на продольные полосы шириной 2Во (рис. 7-3), в которых картина течения повторяет­ся. В дальнейшем рассматривается течение в одной такой полосе.

Согласно опытным данным профили безразмерной избыточной ско­рости в зоне совместного движения в полосе 2£0 подобны и удовлетво­рительно описываются соотношением

В зоне совместного движения из-за выравнивания скоростного поля кинетическая энергия переходит в потенциальную, вызывая повышение давления в потоке. Давление повышается от разрежения в зоне раз­дельного движения до давления в окружающей среде или несколько

118

Выше. Как в зоне раздельного, так, и в зоне совместного движения в по­перечных сечениях статическое давление остается практически посто­янным.

Так как профили скоростей в поперечных сечениях подобны, зада­ча динамического расчета в зоне совместного движения струй на уча­стке двумерного течения сводится к отысканию изменения вдоль потока трех неизвестных величин: осевой скорости ит, минимальной скорости и2 и статического давления.

В основе расчета наряду с указанным подобием полей скоростей положены следующие предпосылки. Пограничный слой на стенках, ограничивающих течение в поперечном направлении, не оказывает влияния на распределение скоростей в струях; трение жидкости на границах между соседними полосами течения отсутствует, поскольку здесь поперечный градиент продольной скорости обращается в нуль; давление в поперечном направлении к потоку постоянно; после слияния струй до сечения хт в плоскости ху при 2=0 расход жидкости посто­янен.

В указанных условиях турбулентное течение несжимаемой жидко­сти в полосе 2Во при стационарности процесса по отношению к осред - ненным скоростям в системе координат, указанной на рис. 7-3, может быть описано системой уравнений движения и неразрывности:

— турбулентное трение.

В выражении (7-88) верхний знак берется при отрицательном по­перечном градиенте скорости, а нижний — при положительном. По­скольку в рассматриваемой задаче ди/ду<С0, то т>0.

Интегрируя уравнения системы (7-87) от нуля - до произвольного значения у с учетом в первом уравнении выражения для V, определен­ного из второго уравнения, приведем систему к следующему, удобному для решения виду:

ЦиЧу-иЦийу=-.у£-^-, (7-89)

О о

У=-ъгилУ- (7-90>

О

Так как при у=В0 V—0, второе уравнение данной системы выра­жает условия постоянства расхода в полосе шириной 2В0, т. е.

&0 О 0

^11йу = 0 или ^Ус1у== сог^. (7-91)

При у=Во соблюдается также условие т = 0, так как градиент ско­рости ди/ду=0. Последнее вместе с условием У=0 позволяет записать

1

В0 + ^ =0 или |ї/*^4-^- = С0П8ї. (7-92)

-0 - о

Уравнение (7-92) выражает сохранение импульса в пределах дву­мерного течения х<хИ2, который равен количеству движения на срезе сопла.

Так как р(у) =сопб1, то из (7-92) можно выразить величину гра­диента давления через изменение скорости

<7-93)

О

Подставляя (7-93) в уравнение (7-89), получаем:

{ - и^иау-£^и°с1у + ^- = 0. (7-94)

Уравнения (7-91), (7-92) и (7-94) образуют замкнутую систему, которая позволяет определить искомые величины: Ыт, £/2, р. Эта зада­ча решается путем перехода от описания поля скорости Д£/=ф(|) к более удобному в расчетах профилю избыточной скорости, предло­женному О. В. Яковлевским [Л. 18]:

8и-= (7-95)

В уравнении (7-95):

G—средняя по площади скорость потока в канале шириной 2Во, являющаяся в силу соотношения (7-91) постоянной величиной, равной

Ж]и*У>

О

9(1) = ~ — безразмерная координата;

И т — и2 о о

1

■г»--- — • /7°— — • П° —• к = — • V— У9т — 1 /7.ар1

* — Вв > и — ё * и т— ё. х — Ва, V— 1-Л. (/УЬ)

В уравнении (7-96):

ХР— координата, отсчитываемая от точки слияния струй;

/т — длина пути смешения;

V — безразмерная избыточная осевая скорость. _

Преобразуя уравнение (7-94), переходя от профиля скорости Ш= =ф(|) к профилю избыточной скорости (7-95) и к безразмерным вели­чинам (7-96), можно получить дифференциальное уравнение, устанав­ливающее связь между одной неизвестной скоростью V и координатой х°, в следующем виде:

^ [УИ© + Л(Е)У1 = - [* ^У]’. (7-97)

Быть записано в окончательном виде (IV
(7-99)
Решение уравнения (7-99) при граничных условиях д?=0, У=У° имеет вид:
11,93(1/® — V) Уоу
1п ^ = Кх>,
(7-100)
Где /С=142,7х2 — константа, подлежащая определению из опыта. По известной величине избыточной безразмерной скорости можно определить осевую скорость ит и минимальную скорость С/г. Осевая скорость
Ип	(7-101)
Где Сел — Ссл/Со. Минимальная скорость в поперечном сечении
С/.		(7-102)
Подставив значение для средней скорости £ и выразив 1]т через V, получим:
(7-103)
Перепад давления между произвольным сечением и сечением, где происходит слияние струй, определенный из условия постоянства коли­чества движения, составляет:
(7-104)
Переход от координаты х° к величине х/Ьо, отсчитываемой от среза сопла, осуществляется по соотношению