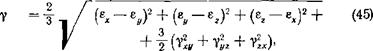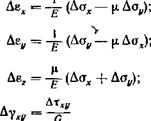СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ

УПРУГО-ПЛАСТИЧЕСКОЕ РЕШЕНИЕ ПЛОСКИХ ЗАДАЧ С НЕПОДВИЖНЫМ ТЕМПЕРАТУРНЫМ ПОЛЕМ ПРИ ПОМОЩИ ЦВМ

При упруго-пластическом решении задачи пластина также раз­бивается на кружки с одинаковыми или различными радиусами. Вначале находят упругое решение в предположении, что пластина бесконечная, не содержит отверстий и свойства металла во всех точках одинаковы. (Упругое решение может быть введено в ЦВМ также после получения его аналитическим способом.)

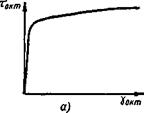
Для упруго-пластического решения задачи необходимо назна­чить свойства металла отдельных зон через диаграммы зависи­мости действительных напряжений от действительных деформа­ций. Для удобства решения эти диаграммы лучше задать в коор­динатах тоюп — уоКт (рис. 22, а):

У 1/ К - + К ~ °г)2 + К - <М2 + <44>

У +6(^ + т^ + тУ>

где у окт — сдвиговая октаэдрическая деформация. 36

Для отверстий и краев пластины задают диаграмму со, = 0 /пис. 22, б). Такие же диаграммы задают для высокотемператур­ных областей, где предел текучести металла также близок к нулю. Для зон со свойствами металла, отличающимися от свойств при комнатных температурах, назначают диаграммы с соответствую­щими значениями G и от (тг).

В ЦВМ направляются и хранятся для каждого кружка: коор­динаты центра кружка х, у, тип диаграммы х0Кт — уокт, компо­ненты деформаций ех, гу, ег, у ху, компоненты напряжений ах, a t %ху. Упруго-пластическое решение задачи проводится за ряд приближений в следующей последовательности. Для каждого

Рис. 22. Диаграммы тжт —у0кт Для различных зон:

а — для материальной зоны; б — для зон отверстий; зон, находящихся за пределами пластины и зон при высоких температурах, где Gj = О

кружка вычисляется уокт по формуле (45) по хранящимся в па­мяти машины гх, еу, ег, уху. Затем по соответствующей для дан­ного кружка диаграмме определяется х0Кт и по формулам (46)— (48) — значения напряжений, соответствующие известным де­формациям:

« *=т^г-

Полученные напряжения ох, а и т могут не соответствовать хранящимся в памяти машины напряжениям ох, оу, тху. Поэтому Для каждого кружка определяются разности напряжений

Ло'=ах-а':

(Д*2 — Дг/2) -— о А~ - + 2Ах Ау Ахх

ху

* ' 2 Дг1 2

1 + Ц 4Д/-2

— (Дх4 — Ау*)Ат^ .

Приращения деформаций вычисляются по известным формулам теории упругости:

(63)

Ах и А у определены в п. 11.

Добавки напряжений и деформаций производятся после опре­деления и запоминания Да^., Дсг^, Дт^ для всех кружков пластины. После суммирования добавок заканчивается первое приближение. Так как при осуществлении добавок нарушается соответствие между ах и а'х, ау и оу, %ху и %'ху, то все операции повторяются снова. Этот процесс приближений продолжается до тех пор, пока разности Да^, Аау и Дт^ не окажутся пренебрежимо малыми.

Изложенный метод решения основывается на теории малых упруго-пластических деформаций, но благодаря использованию ЦВМ позволяет значительно расширить имеющиеся возможности. Снимаются ограничения в отношении равноценности свойств ме­талла |;з различных точках пластины, распределение температуры может иметь практически любой характер.

Однако решение будет правильным, если соблюдаются условия простого температурного нагружения [8]. В противном случае решение необходимо выполнять за несколько этапов, каждый из которых соответствует конкретному промежуточному полю темпе­ратур. При протекании пластических деформаций одному и тому же Распределению нагрузок могут соответствовать различные поля напряжений в зависимости от того, в какой последовательности эти нагрузки прикладывались.