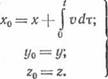СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ

ТЕМПЕРАТУРНЫЕ ПОЛЯ ПОДВИЖНЫХ ИСТОЧНИКОВ НЕПРЕРЫВНОГО ДЕЙСТВИЯ

Полубесконечное тело

Пусть источник постоянной мощности q перемещается с по­стоянной скоростью v вдоль некоторой прямой. В начальный мо­мент t = 0 источник находится в некоторой точке^о0, с которой

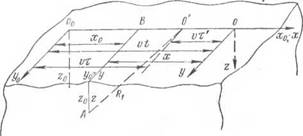
совместим начало неподвижной системы координат (х0, у0, z„). Возьмем, кроме того, подвижную систему координат xyz, начало о которой совмещено с источником и будет перемещаться вместе с ним вдоль оси х0 с постоянной скоростью V (рис. 1).

Координаты любой неподвижной точки А теплопроводящего тела в неподвижной и подвижной системах будут связаны соотно­шениями:

(2.23)

Мгновенное положение источника в неподвижной системе в проме­жуточный момент т определится координатами:

X0 = VT, Уо = 0; z'o — 0. (2.24)

Если граничная плоскость хоу полубесконечного тела непрони­цаема для тепла, то в соответствии с предыдущим элемент тепла 2qdx, внесенный точечным источником в момент т, к моменту і изменит температуру в точке А в неподвижной системе координат на величину

dT(х0, у0, z0, t — т) = -2‘!~—ш-е 40 « -*» (2.25)

V 0,У0 0 ’ су [4па (t — т)] ^ ’ 4

где Mi = (Bo'f + г/о + 2о — квадрат расстояния между мгновен­ным положением источника и рассматриваемой неподвижной точкой А.

На основе принципа независимости действий отдельных теп­ловых импульсов температурное поле к концу действия источника будет найдено суммированием полей мгновенных источников (2.25)

/

Т (х0, у0, z0, t) = dT (х0, у0, z0, t — т). (2.26)

о

Величина (Во'), входящая в (2.25) и (2.26), может быть выражена как в неподвижной, так и в подвижной системах координат. В по­движной системе имеем

(Во') = х + vx' = х - f v (I —- т), (2.27)

в силу чего

Mi = М2 + 2 vx(t — т) + vt — т)2, (2.28)

где

М2 = х2 + і/2 + z2.

При этом соотношение (2.26) примет вид

t

, t Rz ч2 (<—t)

2qe Г dx___ 4a (t - x) 4a

су(4ла)3/2 J (< —t)3/2 Введя новую переменную

1 — t — T

и затем опуская значок~над f, получим

_ t vH

2 а

Из последнего соотношения в силу положительности подынтег­ральной функции при t >0 ясно, что вместе с возрастанием про­должительности действия источника температура во всех точках полубесконечного тела непрерывно возрастает. Как было выяс­нено ранее (п. 3), при длительном действии неподвижного источ­ника постоянной интенсивности температурное поле стремится к предельному установившемуся состоянию. В случае источника постоянной интенсивности, движущегося прямолинейно и рав­номерно, с течением времени температурное поле приближается к установившемуся квазистационарному состоянию, при котором температуры элементов подвижного поля, связанного с источни­ком, в последующем остаются неизменными. Вместе с тем ясно, что температуры неподвижных точек тела изменяются с течением времени. Температурное поле непрерывно действующего подвиж­ного точечного источника, перемещающегося с постоянной ско­ростью v вдоль оси х граничной плоскости ху полубесконечного тела, с учетом теплоотдачи, отнесенное к подвижной системе коор­динат [103], можно представить в виде

Т(х, y, z,t) = ]е 20 ~ 40 dT(х, у, z, т), (2.31)

о

где

dT(х, у, г, т) = cv(42^f)3/2 «ГTS-{] — Ушт[ 1 - Ф (и)] где k — коэффициент теплоотдачи:

z, k ш/-------------

— WS'bVm-<2'32)

Интеграл в правой части равенства (2.31) не выражается через табулированные функции и это затрудняет исследование темпера­турного поля.

Тонкая пластинка

Возьмем тонкую бесконечную пластинку толщиной h, огра­ниченную плоскостями z = 0, z — h. Пусть в начальный момент і = 0 линейный источник находится в начале о0 неподвижной системы координат и с этого момента перемещается в направлении оси х0 с постоянной скоростью V. Примем сначала, что граничные плоскости непроницаемы для тепла. Мгновенное положение источ­ника в момент т в неподвижной системе координат определится соотношениями (2.24).

Температура в некоторой точке (х0, у0) в момент t, вызванная элементом тепла qx dr, введенным в момент т, определится соот­ношением

г

dT(x0,y0,t — x)= 4яТ(Г--^е~4а(<~т) » <2-33)

r21 = (BO’f + yl.

Температуру в той же точке к моменту t окончания действия ис­точника найдем суммированием

t

T(x0,y0.t) =-4^1 (2.34)

Найдем выражение гг в подвижной системе координат. Так как ВО' = x--vx' = x~-v(t — т),

г = г2 + 2vx {t — т) + v (/ — т)2,

Г2 = X2 + у2. При этом (2.34) примет вид

ИЛИ