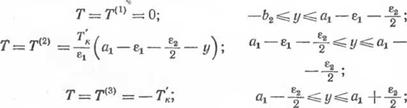СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ
СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ, ВОЗНИКАЮЩИЕ В РЕЗУЛЬТАТЕ СТЫКОВАНИЯ ДВУХ ПОЛОС РАЗНОЙ ШИРИНЫ ПРОДОЛЬНЫМ швом Упругое состояние составной полосы
Суммарную ширину полос обозначим через 26. Пусть е2 — ширина изотермы Тк предельного состояния нагрева, е1 — расстояние между изотермами Тк и Ту того же состояния по нормали к изотерме Тк и к ее огибающей. Примем, что исходные полосы имеют одну и ту же толщину h. Толщина составной полосы в зоне шва, если принять во внимание усиление этой зоны от наплавки, будет больше h. Пусть средняя на ширине е2 толщина этой зоны равна h'. Поместим начало координат в центре тяжести среднего
|
|
|
У |
|
■*> |
|
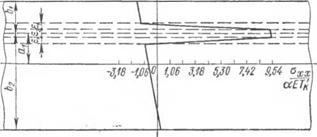
Рис. 29 |
|
по длине поперечного сечения составной полосы с учетом указанного усиления (рис. 29). Обозначим через ах расстояние от оси составной полосы до оси шва. Для решения задачи используем первый метод (п. 29) и первый способ уточнения (п. 31). В соответствии с этим распределение температуры охлаждения по ширине полосы определится соотношениями: |
|
(8.2 ) |
|
|
|
Т — Г(4) = |
|
+ ~2~^ Уі + е1 + |
|
|
|
Т= Т1Б) = 0; |
|
|
|
ai + Ei + ~2~ ^ У *«= |
|
'ь |
Из формул (8.2) — (8.5) получим
охх = 6 Сіу + 2 С2 — а ЕТ. (8.22)
Постоянные Сі и С2 найдутся из условий равновесия внутренних сил в поперечном сечении составной полосы:
f oxxdF = 0-, j аххуdF = 0.
F F
Последние, если учесть, что
ydF = 0; y*dF = Jz,
F F
дадут:
с>=-ш т«№-
F
C, = f. J TdF.
F
Откуда, имея в виду (8.21), найдем:
аЕТ'ка1 (tej +
Сг =
6 Jz
аЕТк (/iBj + h є2)
С% — 2F
Подставив значение Сг и С2 в (8.22), получим аЕТ*
ахх = (heі + h е2) (аУ + г) — аЕТ, (8.23)
Jz
где гг— радиус инерции площади поперечного сечения, а функция Т определена соотношениями (8.21).
Деформация определяется по формулам (8.8), а смещения находятся путем интегрирования уравнений Коши (8.9):
|
(8.24) |
и = — ^ (tej + h) (а. уу + ,*) х
v—-jf (Леі+hE*) [1і +г^) "Ь +
+ а (1 + р) | Tdy.
Из приведенных выражений видно, что поперечные сечения составной полосы остаются плоскими, а ось полосы принимает пораболическую форму, вырождающуюся в прямую линию в случае стыкования полос одинаковой ширины (ах = 0).
Для иллюстрации на рис. 29 приведен график изменения напряжения ахх по ширине составной полосы, где для расчетов принято К = 1,4h; ех = 0,16; е2 = 0,16.
Упруго-пластическое состояние составной полосы
Обозначим через тц и т)2 ординаты границ области пластических деформаций, т. е. примем, что в упруго-пластическом состоянии находится зона т]х ^ у ^ Г)2, где ах — є л — —гр<тіі <3
<3 сі 1 ' 2 » а1 2
пластины находится в упруго-деформированном состоянии. Для деформаций и напряжений в упругой и в упруго-пластической зонах имеем:
упругие зоны:
,(!/)
—■, а остальная часть
о'хух> = 6Сіу - f 2С2 — аЕТ; а(</)
(у) _ JCX_ , т. ехх Р 1 >
(8.25)
|
j(y) хх Е |
Jyi
*УУ
Т=Т{1) = 0; Т
|
где |
|
—Ь2^у^ах- |
|
■F • Єі X’ |
— Iі р~ “Ь СсТ,
|
аі е1 |
Г=Гга = ^-(о, —Є,—Г/);
|
1І2<6'<Яі+Єі + |
|
2 ’ |
Т = 1
|
аі + еі ■ |
Т = Т0) = 0;
упруго-пластическая зона:
|
(8.26) |
«» = ^<« + аГ:
|
р(Р) |
____ Ф п(р) і „71
- 6G + а •
где
SHAPE * MERGEFORMAT
|
7 = 7’<5)=--^-(а1 + є1 + ^-у); fli + %• |
г=Г™ (а.
7 = 7(4) = — 7V;
— - f-;
Єо. ^ і Бо
«і — + -^;
е2
При рассматриваемых нами малых деформациях принимаем, что металл зоны т] і у ^ г] 2 несжимаем и следует схеме идеальной текучести (8.13). Для определения постоянных интегрирования Сх и С2 и параметров ги г]а имеем условия:
|
(8.27) |
} oxxdF = 0; J Ox* ydF = 0;
е[ух (iii) = e(/J (rji);
е{хх (^2) = 4? (дг),
которые, если иметь в виду (8.25), (8.26), дадут систему уравнений:
—6CiSlP) + 2C2F(u) + osF(p) +
aEhT г / о 2
+ —2^— — %) +
4- (ai 4~ єі + — чъ) J = 0;
6Ci (j2 - 4Р)) - 2C2s(/> 4 о'Лр) -
|
aE/iT |
«|з (аі — £і — [тц — (с, — В! — - тр)*] —
|
6є, |
(8.28)
— 2 [т]?—(«і — еі —-JL)3] — 3 (й! + є, + X
X [(а, + е, + - J-)2 - 4] + 2 [(а, + є, + - )* - г, і] } = 0;
бСітц + 2С2 = - J - (1 4- р) ors + аЕТ (тц);
6СіТ]2 4- 2С2 = ~ (1 4- р) os -[ аЕТ (т]2),
где Jz —• момент инерции площади поперечного сечения составной полосы относительно нейтральной оси с учетом усиления, 4Р) — момент инерции площади зоны пластических деформаций, /чр>, s*p) — площадь пластической зоны и статический момент этой площади, F(у) — площадь упругой зоны. При заданных размерах свариваемых полос с учетом усиления зоны шва и заданном режиме сварки, характеризуемом параметрами Ej и е2, можно найти величины Сг, С2, ть, т)2- Тогда деформации и напряжения в отдельных зонах найдутся по формулам (8.25), (8.26), а смещения — путем интегрирования уравнений Коши. Для упругих зон последние будут определяться формулами (8.18).
Вычисления упрощаются в случае полос одинаковой ширины, когда ах — 0. В этом случае, так как г)! = —r2 = т], £>£р) = 0, 176
получим:
сX = 0;
«EhT' , р vs а>(р)
С2_~ 2^(Єі+"2'_гі) ~~2F®>’
где
f(p) = e2A+ 2^--|-)й;
Fly) = 2(fe — г|)А, а величина т] определяется решением квадратного уравнения
|
( |
2е, ос 4 (1 4-ц) е. аД / р„
26 Н М +2fc(£l + -|Ч —
1 а£Гк За£Тк / 2 /
/ , е2у eie2as / h’ , 4(l+p)f>e1o'
-(% + т)— ЇЩГ~’=
На границе пластической зоны можно принять р = 0,5. Тогда, полагая h' — h, можно последнее уравнение привести к виду
г12-26г)-^і + 62-(б-є1--|-)2 = 0.
Нужным корнем этого уравнения будет
*=>-]/Щ+(ь-»-її ■
Отсюда ясно, чем больше полуширина зоны интенсивного нагрева
! + “тгЛ> тем больше ширина зоны пластических деформаций
после остывания. При заданных b, elf є2 чем большее упрочнение получает основной металл зоны шва в результате сварки, тем меньше ширина зоны пластических деформаций после остывания.
