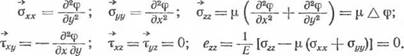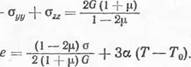СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ

ПЛОСКАЯ ДЕФОРМАЦИЯ

В условиях плоской деформации будет находиться средняя часть призматического тела большой длины, свободного от внеш­них сил и с одинаковым для всех его поперечных сечений неравно­мерным распределением температуры Т (х, у) = Т (х, у) — Т0. Если ось oz совместим с геометрической осью этого тела, то в этом случае получим, что

и = и{х, у) v = v(x, у)

dw dw

(3.42)

дх ду ~ dw.

= const = а;

dz ’

4 Г. Б Талыпов

При этом соотношения (3.7), если учесть (3.20), дадут:

®ХХ — ®ХХ (^» у)

Qyy = (Л'> у) •

= р (а** -J - ада) - j— 2(1 —J— р.) С? [а — а(Т — Т0)];

Тед — Тху (■*'? Р)>

Ttz = Т-уг ~

Третье из уравнений равновесия (3.10) удовлетворяется тожде­ственно, а первые два принимают вид:

Л т« + - ЩЦ + аууї = °-

В силу (3.44) третье из этих уравнений удовлетворяется тожде­ственно. Складывая первые два, получим:

А{Т—7,о) = 0. (3.47)

Если удовлетворено это уравнение, то, как нетрудно убедиться, каждое из первых двух уравнений (б) удовлетворяется в отдель­ности в силу уравнений равновесия (3.44).

Уравнение (3.47) вместе с уравнением равновесия (3.44) пред­ставляют полную систему уравнений температурной задачи теории упругости в напряжениях при плоской деформации. Та же пол­ная система в компонентах перемещения дается уравнениями

(3.46).

Получающиеся в результате решения составляющие переме­щения или напряжения должны удовлетворять соответствующим условиям на поверхности. В частности, если поверхность тела свободна от усилий, то составляющие напряжения на этой по­верхности должны удовлетворять условиям:

(в)

Как показывает формула (3.43), не зависит от г. Поэтому

условие аи = 0 на торцах г = ± цилиндрического тела не

может быть выполнено. Но можно потребовать выполнения этого условия в среднем по поперечному сечению цилиндра

\ozzdF = 0.

Из последнего условия будет найден параметр а. Рассмотрим два метода решения задачи.

Первый метод

Плоскую температурную задачу теории упругости можно свести [59] к решению уравнения Пуассона и бигармоничес - кого уравнения. Как известно, решение обычной плоской за­дачи теории упругости при отсутствии объемных сил сводится

51

к нахождению функции напряжений Эри ф, через которую напряжения определяются по формулам:

й2ф.__________ д2(р ' д2<р

— °УУ—~&Г’ Хху— дхду'

В плоской температурной задаче можно ввести функцию U — (Фі — Т'і). предполагая, что имеют место равенства:

d2U. дЮ. вЧ/ ,0

**— ду2 ’ ~ ах2 ’ Х*У ~~ дхду • W-4®)

Если подставить последние в уравнение равновесия (3.44), то они будут удовлетворены тождественно, а уравнение (3.47) при­мет вид

А Д Ф! - А А 7 + —У--',!1- СА(7-Г0) = 0.

і р,

Отсюда вытекает, что если функция 7 удовлетворяет уравнению Пуассона

Л 7 = ^±^9 {Т - Т0), (3.49)

1 Г

то функция фх должна быть бигармонической

ЛАфі = 0. (3.50)

Если найдены функции Т1 и ф1, как решения уравнений (3.49) и (3.50), то напряжения определяются по формулам (3.48). Эти напряжения должны удовлетворять условиям на поверхности (в). Перемещения определяются интегрированием уравнений Коши. Из соотношений (3.42), используя (3.20) и (3.43), для деформаций получим:

llr = ~W [°хх ~ Е(<К* + °уу) — 2«рС + 2а (1 + р) G (Т — Т0)];

’ll^ = - k'lGvy — ll(0xx + ayy) — 2atiG-f 2«(I+ E)G(7'—Г,,)];

dv, ди Хху

дх ' ду G '

Интегрирование первых двух уравнений дает:

и = ~2С 1 &хх — Е (°« + — 2аЕ° +

+ 2а (1 + р) G (Т — Г0)] dx + (у);

Ц 2(j | Е (^лх “Ь ^да) 2flpG

+ 2а(1 +- e)G(7’— 7,0)]d^ + f2(x).

Подставив (3.51) в третье из уравнений (г) и интегрируя, получим

її (У) — Ау В

/2 (х) = —Ах + С,

где А, В, С — произвольные постоянные интегрирования. Отсюда следует, что члены /у (у) и /2 (х) учитывают лишь жесткое смеще­ние всего тела и на относительные деформации не влияют. Таким образом, для определения деформации можно использовать фор­мулы (3.51) без членов /і (у) и f2 (х).

Второй метод

Если введем потенциал F {х, у) термоупругих перемещений, не зависящий от г:

то система (3.46) будет приведена к одному уравнению

, = — 2 aG

Таким образом, если найдена функция F как решение урав­нения (3.53), то соответствующие смещения, деформации и на-

пряжения определяются по формулам (3.52), (3.55), (3.56). Полу - .ченное решение справедливо тогда, когда на боковой поверхности тела заданы компоненты напряжения, oy°J, гi°J, которые совпадают со значениями напряжений (3.56) на этой поверхности. В общем случае значения напряжений на поверхности тела могут не совпадать с их заданными значениями ахх, ofy, r(x°J. Напри­мер, на практике чаще всего встречаются задачи, когда боковая поверхность тела свободна от внешних усилий, т. е. ax°J = О, °уу = 0, гXJ = 0 всюду на этой поверхности. В таких случаях оказывается необходимым найти такое решение уравнений теории упругости, которое на торцовых плоскостях тела удовлетворяет

условиям w = 0, ххг = хуг = 0, на боковой поверхности напря­жения равны по величине и обратны по знаку тем, которые опре­деляются формулами (3.56) на этой поверхности. Это обычная задача теории упругости и в данном случае она решается при помощи функции напряжений Эри, которая удовлетворяет диф­ференциальному уравнению

Если функция (р найдена, то напряжения, удовлетворяющие заданным условиям на боковой поверхности, определяются по формулам:

— -> Q2

°хх — ахх + °хх = - ЩЇ (ф — 2GF)-, °уу = °уу 4~ °уу — (ф 2GF)

^ху — Тед “Н тед — дхду ( ф “Ь 2G/7)',

О» = Оа + а„ = л (РФ — 2 GF) =

= Р (L + Оуу) - 2аС -1±£ (Т - Т0).

Используя теперь (3.57) и имея в виду, что

О = <УХХ + Оуу + c„ = (1 + р) Л Ф — 4G Д F-,

&F = -±!~a(T-T0),

получим:

= -w{-W— ^Лф)

d2F

(3.58)

^■=ЖЗї{-'а+2Г')'

дх ду

&гг — Ухг = Ууг = 0.

Перемещения найдутся путем интегрирования дифференциальных

dv ди, дь,0 спч

= е„„ — + — = уху. (3.59)

дх ~хх' ду уу’ ду 1 дх Рассмотрим частный случай. Если принять

Ф = 2 GF

как функцию напряжений Эри, то соотношения (3.57) дают:

охх — оуу — тху — 0,

оя = - 2 (1 - Р) G A F = — 2(1 + ц) Get (Г-Т0)-

е*х = ~2G Л - р) + - дрт = 0 р) Л F =

= (1+р)а (Т-Т0); еуи = { +р)а(7’ — 7’0); є2г == 0, уху — 0.

Таким образом, напряжения охх, оуу, хху в этом случае равны нулю везде, а в точках торцовых сечений возникают напряжения сжатия а„.