СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ

ОПЫТНОЕ ОБОСНОВАНИЕ ОСНОВНОЙ ГИПОТЕЗЫ

Деформации и напряжения однослойных полос с заделанными концами, подвергнутых сосредоточенному нагреву посередине длины, после последующего остывания

длины этой полосы до Т <* Тк недопущенные температурные де­формации этого участка обратятся в деформации сжатия всей полосы. Если эти деформации сжатия упругие, то после после­дующего остывания полоса будет свободна от напряжений.

При достижении температуры Т = Тк в более нагретой части этого участка длиной ах температурные деформации как этой части полосы, так и всей остальной части обратятся в пластические деформации участка аи и продольные напряжения в полосе будут отсутствовать. В этот момент пластическая деформация сжатия участка ох будет состоять из недопущенной температурной де­формации а (Тк — То) самого участка сх и его пластической де­формации сжатия е<Р> от температурного расширения смежных с ним участков полосы.

При дальнейшем повышении температуры участка аг до Т >- Тк будут повышать свою температуру смежные с ним части полосы, причем температурные деформации как более нагретых, так и менее нагретых частей полосы будут происходить за счет пласти­ческих деформаций более нагретых частей, где Т ^ Тк. Обозначим через а ширину изотермы в этом состоянии. Обратные температур­ные деформации остывания как более нагретых, так и менее на­гретых частей полосы будут происходить за счет обратных пла­стических деформаций более нагретой части без ее сопротивления до тех пор, пока температура в этой части не выравнится до Т = = Тк. Поэтому в предельном состоянии нагрева активная часть пластических деформаций зоны интенсивного нагрева определится соотношением

а(Тк-Т0) + ?р (7.1)

где е<Р> — пластическая деформация сжатия участка а, вызван­ная температурным расширением смежных с ним частей полосы. Если в этот момент участок а вырезать из остальной части полосы,

то к моменту своего остывания до начальной температуры Т0 он получит относительное укорочение (7.1). Но с момента выравни­вания температуры до Т = Тк материал этого участка приобретает способность сопротивляться деформациям и в силу несвободности последующих температурных деформаций к моменту полного осты­вания пластическая деформация (7.1) будет компенсирована за счет деформации растяжения всей полосы.

Примем далее, что величина а (Тк — Т0) составляет главную часть пластической деформации участка а к моменту выравнивания температуры внутри него до Т = Тк при остывании. Величиной в тот же момент по сравнению с а (Тк — Т„) можно пренебречь. При этих условиях, если принять металл полосы однородным, основная гипотеза при применении второго метода для относи­тельного удлинения в точках полосы после ее полного остывания дает

ехх = -(Тк~-о)-а. (7.2)

Для опытной проверки этого положения были подвергнуты сосре­доточенному нагреву полосы из сталей типа СХЛ, 4С, 1Х18Н9Т, сплава АМГ-6Т и двухслойные полосы с основным слоем — сталь 4С и плакирующим — сталь 1Х18Н9Т. Ниже излагаются результаты этих опытов.

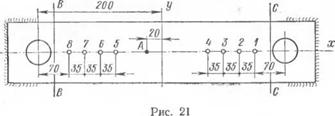
Сталь типа СХЛ. Сосредоточенному нагреву до Т> 640° С была подвергнута средняя часть каждого из образцов 3 и 4, имею­щих поперечные размеры 50 X 7 мм (рис. 21). Концы этих образ­цов при помощи болтов, а также лобовых и фланговых швов (рис. 21) прикреплялись к стальной болванке с поперечными раз­мерами 220 X 220 мм. После полного остывания средняя часть каждого из них подвергалась мощному нагреву, так чтобы были

дТ дТ г, дТ.

выполнены условия - — 0, ■ д~ =£ const, до темпера­

туры Тк на расстоянии 20 мм от середины длины, где температура контролировалась термопарой А. У образца 3 термопара А по­казала максимальную температуру Т = 720г С, а у образца 4 — 640° С. После нагрева и полного остывания к этим образцам в их закрепленном состоянии приклеивались датчики 1—8 сопротив­ления в соответствии со схемой на рис. 21. Затем после сушки и контроля показаний датчиков снимались начальные замеры. Последующие замеры снимались после того, как образец был от­делен от болванки путем вырезки на строгальном станке по ли­ниям ВВ и СС. Данные этих замеров, а также соответствующие деформации приведены в табл. 6.

Таблица Є

Нагрев этих двух образцов производился в холодном поме­щении так, что для образца 4 без особой погрешности можно при­нять Тк — То = 640° С при а = 40 мм. Формула (7.2) для этого образца дает

4-12.5-К)-6-640 спп 1П_6

=---------------- 40---------------- =----- 80°- 10 •

что практически совпадает с опытными значениями деформации того же образца в средней части его длины. Опытные значения де­формации вблизи концов у этих образцов несколько занижены,
что можно объяснить влиянием начальных напряжений от при­варки их концов к болванке и влиянием концентрации напряжений около болтового отверстия. Датчики охватывают почти всю длину полосы с двух сторон от зоны нагрева (рис. 21). Замеренные по показаниям этих датчиков деформации практически одинаковы по длине каждой из этих полос за исключением одной выпавшей точки у образца. Из этого следует, что принятый способ нагрева не вызвал изгиба этих полос. Опытные значения деформации у об­разца 3 оказались несколько большими, чем у образца 4. Этот факт объясняется тем, что длина зоны нагрева до Т ^ Тк у об­разца 3 была больше чем у образца 4.

Сталь 4С. Для опытов были взяты полосы 1 и 2 толщиной 5 мм, шириной 50 мм и длиной 500 мм. Концы полос прикреплялись к жесткой болванке в соответствии со схемой на рис. 21. Как по­казали проведенные опыты [96], за температуру Тк этой стали можно принять Тк = 700° С. Нагрев средней части каждой из этих полос осуществлялся изложенным выше способом в соот­ветствии с законом

дТ1 , /л. дТ дТ ^ Г7 41

до Т = Тк с ■ 700° С на расстоянии 10 мм от середины полосы 1 и на расстоянии 15 мм от середины полосы 2. Изменение темпера­туры в точке х = 10 мм во времени записывалось на осцилло­графе МПО-2. Деформации полосы замерялись ранее описанным способом. Результаты замеров даны в табл. 7.

Таблица 7 Таблица 8

Остаточные деформации ехх - 10е Остаточные деформации ехх-10в

образца из стали 4С образца из стали 1Х18Н9Т

Сравнивая последние с данными табл. 7, видим, что основная гипотеза для стали 4С дает удовлетворительный количественный результат.

Сталь 1Х18Н9Т. Опыты [96] показали, что за температуру Тк этой стали можно принять Тк н = 850° С. Нагрев полос 1 и 2, имеющих размеры 500 X 50 X 5 мм, осуществлялся изложенным выше способом в соответствии с законом (7.3) до Т = 850° С на расстоянии 10 мм от середины длины. Результаты опытов при­ведены в табл. 8.

По формуле (7.2) при ан = 18,6-10'® [96], Тк-Н — 850° С, I — 400 мм, а = 20 мм получаем ехх — 790-10“®, т. е. в этом случае основная гипотеза также дает удовлетворительные коли­чественные результаты.

Сплав АМГ-6Т. Проведенные нами опыты показали, что за тем­пературу Тк для этого сплава можно принять Тк = 375° С. На­грев средней части длины полоски этого сплава, имеющей раз­меры 500 X 50 X 6 мм, осуществлялся угольным электродом в соответствии с законом (7.3) до Т = 375° С на расстоянии 10 мм от середины длины. По показаниям датчиков сопротивления было получено ^«=*400-10“®. По формуле (7.2) при а = 25-10“® [130], Т = 375° С, а = 20 мм получаем ехх = 470-10“®, т. е. основная гипотеза для этого сплава также дает удовлетворитель­ные количественные результаты.

Деформации и напряжения двухслойной полосы со свободными концами,

подвергнутой сосредоточенному нагреву посередине длины, после последующего остывания

Исследование остаточных сварочных напряжений (деформаций) в биметаллических балках на основе гипотезы плоских сечений дано в работе [56]. Приведенные в этой работе опытные значения прогибов значительно отличаются от расчетных. Насколько из­вестно других опубликованных работ по исследованию сварочных деформаций (напряжений) в изделиях из биметаллов нет, но имеется ряд работ, посвященных разработке технологии сварки такою рода изделий.

Ниже дается теоретическое решение задачи на базе основной гипотезы и опытная проверка результатов.

Теоретическое решение. Пусть ан — среднее значение коэф­фициента линейного расширения металла нержавеющего слоя в рассматриваемом интервале температур; ас — коэффициент ли­нейного расширения металла основного слоя; Тк н — температура, при которой металл нержавеющего слоя теряет способность сопро­тивляться пластическим деформациям; ТКшС — та же температура для металла основного слоя. Обычно Тк н >> Тк с. Принятое здесь условие крепления концов при сосредоточенном нагреве средней части длины полосы обеспечивает свободу продольных темпера­турных расширений. Обозначим: 2ах — ширина изотермы Ткн;

= _JL (ЗСці/, + 2Ciiy) _ _зс^_ +

+ (1 + И J <*Т (У) dy + АцХ + П12;

х Z/2:

<з^хх — 6С22У - Ь 2Сгії 2х

(ЗС22 -(- С21) Л22у - j - П22;

vV2> = -4 (3 С22у2 + 2С21у) —+ л22* + п21;

условия:

п(1) (0,0) = 0; ц(1) (0,0) = 0;

и">(аь 0 ) = «rafo,0); f0’ (й2, 0) = vm (а,, о);

dv*9 dv^

ЛГ-sr прн * = у = ();

\o(^dF=\o^ydF^Q -

J | a(x2J df= jj a(x2J ydF = 0;

для постоянных интегрирования дают:

Ап = £)xl = Du = 0;

На основании (7.9) по формулам (7.4)—(7.7) для напряжений и деформаций в отдельных зонах получим: зона 0 х sg а2:

ail? = -(а"-.а^ ^ ~Н,)ЕТк с [3 (А + hx) у — 2h%

— Лх< y=ssA; т(і) _ (а« — ас) (А 4- Aj) £ТК.

[3(A-Aj)y + 2A*],

4й3

— A=s= !/==£ —Лх;

„<ч= W. (з^-с) (tf-tf)»-

— 2Л2 [ак (Л — Аі) + ас (Л + Аі)]};

ит = Щс_ {з{ан_ас) (h*_л?)у_

— 2 [сс„ (ft — hi) - f ас (ft - f - hi)] ft2}; о<2) (л; 0) — 3 (а" ~ Ис) °2 (ft2 — лі) гк. t (а2 — 2х)

Опытная проверка. Для опыта использована биметаллическая полоса из сталей 4С и 1Х18Н9Т длиной I = 300 мм, шириной b = = 50 мм, с общей толщиной 2ft = 8,8 мм при ftx = 1,8 лш. На-

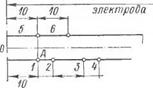
грев средней части длины полосы осуществлялся быстрым пере­мещением электрода по ее ширине в прямом и обратном направле­ниях со стороны плакирующего слоя. Для измерения темпе­ратуры использованы термопары хромель — алюмель, которые приваривались в выбранных точках полосы как со стороны плаки­рующего слоя, так и со стороны основного. На рис. 22, а дана схема установки термопар, где 1, 2, 3, 4 — термопары со стороны плакирующего слоя, а 5—6 — со стороны основного слоя. Термо­пары были подключены к осциллографам МПО-2, и в процессе нагрева на пленке записывались Т (і) в каждой выбранной точке. На рис. 22, б приведены температурные кривые со стороны основ­ного слоя (1) и плакирующего (3) для того момента времени, когда температура в точке А имеет максимальное значение, близкое к Тк н. Там же нанесена кривая (2) средних по толщине полоски температур в тот же момент времени. Из этой кривой имеем аг = = 8 мм, а2 = И мм - П° формулам (7.10) и (7.11) подсчитаны про­гибы полосы при ас = 14,4-10_6, ан = 18,6-10~6, Тк с = 700° С,

Тк. н — 850° С, I = 300 мм, 2/г = 8,8 мм, Л3 = 1,8 мм, ах = 8 мм, = 11 лш и построена кривая прогибов, приведенная на рис. 22, в. Там же нанесены замеренные значения прогибов. Сравне­ние теоретических (•) и опытных (о) значений прогибов показы­вает, что основная гипотеза для биметаллов дает удовлетворитель­ные количественные результаты.

Деформации и напряжения двухслойной полосы с заделанными концами, подвергнутой сосредоточенному нагреву посередине длины, после последующего остывания

Теоретическое решение. Обозначим через аг и ct2 радиусы изотермических поверхностей Ткн и Ткс предельного состояния нагрева, на которых металлы плакирующего и основного слоев теряют свою способность сопротивляться пластическим деформа­циям. В этом состоянии внутренности этих поверхностей имеют соответственно активные пластические деформации сжатия в про­дольном направлении:

ан(ТК'Н—Т0у,

ае(^к. с Т0).

Коэффициенты линейного расширения, как и раньше, будем считать постоянными. В этом предельном состоянии полоса прини­мается свободной от напряжений, и последние возникают лишь в результате остывания до Т0 внутренностей указанных поверх­ностей Тк н и Ткс. Поэтому задачу в первом приближении можно сформулировать следующим образом: определить деформации и напряжения исходной полосы, возникающие в результате ее охла­ждения от нуля по закону:

В силу симметрии достаточно рассмотреть правую половину полосы 0 х «S 1/2. Для напряжений и перемещений в отдельных зонах в соответствии с (3.81), (3.84) получим: зона 0 sg х сіх-

°хх = 6СпУ f - 2Сіг — и-ЕТ (у)] u(1) = (3 СххУ + с12) - АххУ + Dxx,

y<1> — тг (ЗСДг/2 + 2С1гг/) •

аТ(у) = — анТк. н — —ТК'Н, —h^y^ — hu af(y) = — acTK, c = — fK, ct —t/<s£ Л;

зона ох

Охх 6С22// + 2С21 — а£Г (у);

„(2) = ^ (ЗС22г/ + Сп) - Л22у + D22;

о<2> = - (ЗС22у2 + 2С21г/)------------------ +

+ (1 + (i) j аТ(у) dy + A22x + Da,

0 при д: = 4-, г/ = 0

J j oiVdF = j j o^dF = J J <&dF = 0; j j o(^xydF = j J OxlydF = j J o^ydF = 0,

для напряжений и перемещений в отдельных зонах зона 0 sg х «s; с3:

ОЙ = ± £с£0«2 (КТК. н-Тк. с)У~

— (KxhJ 'к.« ~Н 7^. с)] +

+ н “Ь ЕТК с

■— h^y^ — hx — hx^y^h и(1) =_3

2_ аоаг (/'і Е{ГК н Гк. с) х;

„(!) = _ (Л2ГК. н-Т, е) (ру2 + х2) +

+ ~2~ Уаоа2 (ККТк-нЛ~ Т'к. с) У +

+ ^Ш1 ^fK. « - «Л. с) -

(1 + И) Т'к. нУ (1 + F) Тк су

— h sc у eg — hx — hx^y^h зона а^х^йоГ

т<2) ЗЕар^Щ ( 2at Tf, ~

4h 1-2а2 ‘к-нА-*к. с)У--

+ 2 Еа0а2 (^ — 2с^ Тк. н Тк-с) рТк. с;

— Л 3 sg у sc h

иі2) = -^г-{т^^н+^)Ху+

+ ~2 аиа2 ( 7 — 2а2 Тк. к — Тк_ X +

+ - і-а1а17’к. с(-?М—2);

(2) _ ЗраоИЩг / 2аі р 4- Т 2__

8Л 1 — 2аг к-н'1к-с)У

Y^a°as ( 1 —Х2а2 Тк. н Тк_ с) у +

і Залщаз Г а1(1 — 2х)2 тр.

^ 16Л L / — 2а2‘ 7 «■« г

+ 2 (х2 - 4 а2і) тк;с] - (1 + р) Тк_ су;'

— hx^y^h

„(З, = ££ {аітк н - а2Тк с) (/ -2х) у - - («ЛТк. н + а2Тк. с) (І - 2х);

Опытная^проверка. Опыты для двух биметаллических полос из сталей 4С*+ 1Х18Н9Т с заделанными концами были поставлены точно таким же образом, как это описано выше. Кривые Т (х) для этих двух полос дали ах = 1,1 см, а2 = 1,2 см. Для теорети­ческих значений ехх по третьей из формул (7.20) имеем

При h — 0,44 см, hx = 0,18 см, I = 40 см, Тк-Н 18,6-10 6-850, ТКшС— 14,2-10_6 -700 получаем:

eS (/*)=-400 -10~'6; *?£>( — h)= 1000-10~6.

Результаты замеров при помощи датчиков сопротивления при­ведены в табл. 9.

Кроме того, пользуясь третьими из формул (7.18)—(7.19), можно построить линию прогибов полосы v (х, 0), которая для рассматриваемых полос приведена на рис. 23 (•). Там же нанесены замеренные значения прогибов (о). Полученные результаты под­тверждают факт, что основная гипотеза дает удовлетворительные количественные результаты и в случае биметалла.

Применимость основной гипотезы к определению сварочных де­формаций и напряжений в биметаллах позволяет утверждать, что основная гипотеза с достаточным основанием может быть исполь-

0 50 т і50

X, А7М

Рис. 23

зована для определения сварочных напряжений и деформаций в изделиях, сваренных из разнородных металлов [41, 65], имею­щих различные теплофизические и физико-механические харак­теристики.

Основная гипотеза справедлива для любого материала, кото­рый при местном сосредоточенном нагреве до достаточно высокой температуры способен перейти в этой зоне в чисто пластическое состояние. При этом, имея опытную кривую 0S (7), можно откор­ректировать значение температуры Тк этого материала при помощи простых опытов (рис. 21).

Деформации и напряжения в точках листа, подвергнутого сосредоточенному нагреву в центре, после последующего остывания

Теоретическое решение. Попытка решения задачи определения деформаций и напряжений в точках листа, возникающих в про­цессе его нагрева в центре, как температурной задачи теории упру­гости была сделана в работе [60]. Рассмотрим деформации и на­пряжения, возникающие в точках большого листа после мощного сосредоточенного нагрева в центре и последующего остывания.

Если температура нагрева Т ^ Тк имела место внутри и на контуре круга радиусом г = а, то в соответствии с основной ги­потезой можно принять, что к моменту выравнивания температуры внутри этого круга до Тк последний получит пластическую де­формацию сжатия

и^ = а(Тк — Т0)а = ае]Р (7.21)

обусловленную несвободностью его температурных деформаций нагрева. Другими словами, если этот круг в указанный момент (Т = Тк на а) вырезать из остального листа, то к моменту полного остывания его радиус уменьшится на величину, опреде­ленную по (7.21). Но в силу стесненности деформации при после­дующем остывании полученная этим крутом при подогреве пла­стическая деформация к моменту полного остывания будет ком­пенсирована как за счет деформации части листа, где г ==g а, так и за счет деформации его части, где г а. При этих условиях задача определения приближенных значений деформаций и на­пряжений листа после его нагрева и остывания сведется к опре­делению деформаций (напряжений) составного листа, получаю­щегося в результате сшивания диска радиусом а, с листом с круго­вым отверстием радиусом а. Условиями сшивания будут:

и<Х) (щ) + | и(г2) (а) | = и‘р);

П К1'**)

Or (ai) = Or (а),

где ц*Х) (Gj) — радиальное перемещение точек контура диска; и}2) (а) — радиальное перемещение точек контура отверстия листа.

Рассмотрим эту задачу.

1. Деформации и напряжения диска. Последующие расчеты проведем применительно к стали типа CXJ1, используемой в со­стоянии поставки (без термообработки) для наружной обшивки корпуса корабля. Как показано в п. 25, в зоне термического влия­ния предел текучести os стали типа СХЛ после сварки в состоянии поставки приблизительно на 30—35% выше ее предела текучести вне зоны термического влияния. Поэтому можно принять, что материал диска г ^ at не может перейти в пластическое состояние. Данное утверждение будет полностью оправдано ниже. Этот диск, получивший при нагреве пластическую деформацию (7.21), при последующем понижении его температуры от Т = Тк до началь­ной будет подвергнут равномерному растяжению. В этом случае, как легко убедиться, радиальное перемещение точки контура опре­делится формулой

н'1)(а1) = 1^аЮо, (7.23)

где а0 — неизвестное радиальное напряжение в точках контура.

2. Деформации и напряжения вне круга г = а. В зависимости от величины е(гр) и, следовательно, о0 вне круга г — а могут быть и пластическая и упругая области. Предположим, что некоторое
кольцо a г ^ b находится в пластическом состоянии, а осталь­ная часть листа г ^ Ъ — в упругом состоянии.

Упругая зона (г 5» Ь). Смещения в этой зоне опреде­ляются формулой

ц<3> = Лг + А.

Так как (оо) = 0, то должно быть А = 0 и, следовательно,

ц<3) — А ґ

Из условия Губера—Мизеса в этом случае

о ЛЬ)'

Имея в виду, что

(1 + (і) *

получим

В=-Ж64

(7-24)

°'=Тї(Я’ <7-25)

кроме того, уравнение равновесия дает

(7-26)

Пластическая зона (а г ^ Ь). Используем усло­вие пластичности Губера—Мизеса, которое в данном случае в силу полярно-симметричности задачи пишется в виде

(о, + се)2 + 3 (ov - со)2 = 4с2 = 12k1.

Оно будет удовлетворено тождественно, если примем:

or — 2^cos ^ ;

v ce = 2£:cos(p + -|-),

где Р — новая переменная.

Подставив последнее в дифференциальное уравнение равнове­сия, получим:

(КЗ — ctg р) rfp = 2 ,

откуда

, _ Ае(7.28)

sin Р

С другой стороны, пренебрегая сжимаемостью материала, из ус­ловия коаксиальности главных деформаций и приведенных на­пряжений получим

duf> 42)

dr г

2сг~ав _2(°е-аг) ’

где: 2°Г — = 2* Sin( р + ^;

2ае — ог— — 2 |/ 3 k sin f р ^ ,

в силу чего

d„<2> sin(P f іг) dr

«(2) /и Я 6 '

51П(Р-т)

Из соотношения (7.28) будем иметь

(»-т)

sin

2г — = 2ra___________

dp z sin p

или

. sin dr

ф.

Л sin P

Подставив последнее в выражение (7.29), получим ~~Ш~ = — у (КЗ + ctg р)ф.

Общим интегралом этого дифференциального уравнения будет

(п<2))2= е- ^р _ (7.30)

' 7 Sin Р ' 7

Рассмотрим теперь граничные условия для переменной р. При г = а ог — ав и поэтому в соответствии с первой из формул (7.27) для главного значения Р будем иметь

о и і о» 2 . On

р = т + arccos = 3- я - arcsin - JL.

С другой стороны, на границе упругой и пластической зон при г = b имеем:

Уз

с0 =--------- — 2k cos

0 Гз

Откуда следует, что на этой границе

стг + °е = О

и, следовательно,

Р = т-

Таким образом, интервалом изменения р будет

Тл — arcsin-^-. (7.31)

Постоянная А в выражении (7.28) будет определена из условия, что при

о 2 . Од

р = у я — arcsm-^-

имеем

Г = а,

т. е.

!и.(|я_аиіп^)=-^(Іії+і7, _

поэтому для А получим

Щп+V^-^) х

X ехр Г— Кз^л — arcsin^-^j.

Таким образом, зависимость между г и р будет представлена соот­ношением

А =

T(fr+^«)-P [^3(Р-4л + агС5іпж)] •

(7.32)

Перемещения в пластической зоне определяются по формуле

(«<2)>2 = ехр (— КЗ р). (7.33)

ядро будет находиться в упруго-пластическом состоянии. Этот вариант рассматриваемой задачи также может быть решен без особых затруднений.

Зная а0, можно найти деформации и напряжения в любой точке рассматриваемого листа. В соответствии с формулами (7.23), (7.24) и (7.34) для относительной радиальной деформации имеем:

0 =

(7.37)

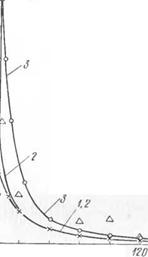
где р и г связаны соотношением (7.32), а величина b определяется по формуле (7.35). По этим формулам, имея в виду границы из­менения переменной р (7.31), можно построить график изменения радиаль­ной относительной деформации в зави­симости от радиуса. На рис. 24 приве­дена кривая 1 при а = 20 мм а0 = = 4525 кПсм2 без учета упрочнения в кольце a sg г ^ d, где d — наруж­ный радиус мелкозернистой зоны (п. 31).

Опытная проверка. Для проверки этих результатов центральная часть квадратного листа № 22 стали типа СХЛ (450 X 450 X 10 мм) была ПОД-

t80 г, мм

вергнута сосредоточенному нагреву до 620° С на расстоянии 20 мм от центра. Для обеспечения равномерности темпе­ратуры по толщине листа подогрев производился с обеих сторон. Датчики были приклеены до нагрева на определенном расстоянии от зоны нагрева в соответственных точках с обеих сторон листа, так что они фиксировали лишь упругие деформации. Вблизи зоны нагрева деформации измерялись оптическим компара -

тором по изменению расстояния между точками, помеченными острым керном. Относительные радиальные деформации в точках этого листа, замеренные датчиками сопротивления и оптическим компаратором лаборатории, нанесены на рис. 24 значками Д. Аналогичные результаты были получены повторными опытами при нагреве до Г = 620° С на расстоянии г = а = 30 мм от центра. Сравнение результатов, полученных теоретически на базе основ­ной гипотезы и опытным путем, показывает, что они достаточно хорошо совпадают при больших г. Поэтому некоторое превышение опытных данных над теоретическими, полученных вблизи вну­тренней границы наружной упругой области, нельзя объяснить тем, что теоретические значения получены для бесконечной пла­стины, а опытные — для конечных. Но вместе с тем рис. 24 пока­зывает, что основная гипотеза правильно определяет приближенно состояние листа после последующего остывания.