СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ

МЕТОД ТЕОРЕТИЧЕСКОГО ОПРЕДЕЛЕНИЯ СВАРОЧНЫХ ДЕФОРМАЦИЙ И НАПРЯЖЕНИЙ

2. Определение деформаций и напряжений в неравномерно

нагретой полосе

Из приведенных выше данных видно, что при сварке имел место неравномерный нагрев деталей, резко сконцентрированный в месте наложения шва. Поэтому для возможности определения деформаций и напряжений при выполнении различного рода сварочных работ необходимо установить метод определения де­формаций и напряжений полосы с неравномерным распределе­нием температуры, подвергающейся нагреву или находящейся в процессе остывания. Первый из указанных случаев рассмотрен в‘настоящем параграфе.

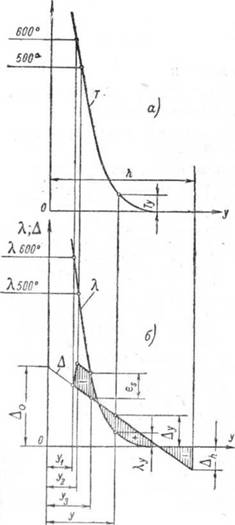
В случае неравномерного нагрева полосы можно для опре­деления деформаций и напряжений воспользоваться положениями, полученными для случая равномерно нагретого стержня, если рассматривать отдельные продольные волокна неравномерно на­гретой полосы, как равномерно нагретые стержни с ограничен­ной свободой перемещения. Так, например, если для некоторого сечения полосы распределение температуры по ширине полосы может быть представлено кривой Т (рис. 24, а) то относитель­ные тепловые удлинения отдельных продольных волокон полосы (если предположить их независимыми друг от друга) изобра­зятся кривой X (рис. 24, б). Так как действительные деформации каждого волокна зависят от деформации всех других волокон, причем для деформаций полосы с достаточной для практики точностью можно признать справедливой гипотезу плоских сече­ний, то действительные деформации изобразятся не кривой Х, г а прямой Д (рис. 24, б).

Вследствие несовпадения кривой X и прямой Д в полосе воз­никнут напряжения, зависящие от разности между той деформа­цией Х^,, которую имело бы данное волокно, если бы свобода его удлинений ничем не была ограничена, и деформацией Д^,, которую получило данное волокно в действительности, т. е.

оу = Е (Д_,, — у) = Е - &у.

Напряжения могут быть как сжимающие (при )^>Д>,), так и растягивающие (при Д^>Х^).

З Н. О. Окерб. юм. 2381- 33

Нели относительные деформации еу для любого волокна меньше деформаций є5, соответствующих пределу текучести, то во всех волокнах будут существовать только упругие деформа - У оо ции, и напряжения ау бу­

дут меньше as — предела текучести.

Если для некоторых во­локон по абсолютной величине больше es> то бу­дут существовать и упругие деформации, равные и пластические деформации

«ПЛу

епл-у “

“IV-l,*l”l4r—XjJ-_l**l-

В этом случае эпюра напряжений в рассматривае­мом сечении полосы будет иметь тот же вид, что и эпюра упругих деформаций (заштрихованная площадь на рис. 24, б).

В зависимости от вели­чины упругих и пластиче­ских деформаций вся ши­рина полосы может быть разделена на четыре уча­стка. На участке от^8 до h (рис. 24, б) имеют место только упругие деформа­ции, так как

Ьу—

Соответственно напря­жения на этом участке

3y = E{by—y)<oS'

На участке полосы от У2 ДО Уз> где температура нагрева меньше 500°, но Aj, — упругие дефор-

постоян-

На этом участке, кроме упругих, имеют место и ские деформации.

На участке от ул до у, у где температура меняется от 500 до 600° имеют месі о и упругие и пластические деформации, при этом напряжения равны

° У ~ = °st

где e's — относительные деформации, соответствующие пределу текучести при температуре того или иного волокна и меняю­щиеся от (при Т = 500е) до 0 (при Т = 600°).

Наконец, на участке от 0 до уи где температура нагрева выше 600°, имеют место только пластические деформации.

При этом Оу ~= 0, так как о' = 0и е^ = 0-

Ввиду того, что в рассматриваемом сечении внешние силы не приложены, что все внутренние силы должны находиться в рав­новесии, т. е. сумма - всех внутренних сил и сумма моментов этих сил относительно любой точки должны быть равны нулю, что равносильно выполнению следующих двух уравнений:

Л А

J С ydy = 0; jcyydy = 0. (1)

о 0

Если в уравнения (1) подставить вместо су их значения, выраженные через є, то получим (после выполнения интегри­рования на участках уг -*-у2 и у*-*-уз следующие выражения:

1 " Л — т O'»—Л) — *s O'» —Л) + j (Л, — i-y)dy = 0;

У3

— l2es (уі — Уі) уі + - Уі) [у2 + 5 СУ» - У*}+

А

+ {&у — 'ку)уйу = 0, (2)

из которых могут быть определены три неизвестные величины j/8, Д0 и ДЛ, если добавить третье уравнение, непосредственно вытекающее из рис. 24, б:

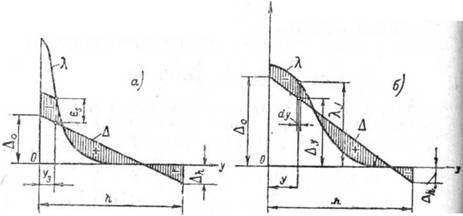
В тех случаях, когда эпюра распределения температуры не содержит участков с температурой, превышающей 500°, эпюра деформаций значительно упростится и будет иметь вид, пред­ставленный на рис. 25, а. Соответственно упростятся и выраже­ния (2), которые примут следующий вид:

А

“ Уь es ~Ъ I (Ay— dy = 0;

.Уз

-T-s*+ ](by — by)ydy = 0. (2")

.Уз

Если при нагреве полосы не свыше 500° кривая распределе­ния температур будет достаточно пологой, так что нигде на всей

ширине полосы не появятся пластические деформации (рис. 25, б), то выражения (2) напишутся в следующем виде:

| (Л,—)dy = 0; | (Д, - X, )ydy = 0. (2")

о о

При заданной функции Х=/(у)и имея ввиду, что

А. у = Д0

совместное решение двух уравнений (2') позволяет определить две неизвестные величины Д0 и ДЛ, определяющие положение пря­мой Д и величину упругих деформаций и напряжений.

А;Д

Таким образом, если известно распределение температуры в рассматриваемом сечении, то могут быть определены действи­тельные относительные деформации Д и кривизна С полосы в дан­ном сечении:

г ah

" А »

а также упругие деформации любого волокна и пластические деформации, вызванные как температурой, так и механическими воздействиями остальных волокон на данное.