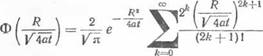СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ
ИСТОЧНИКИ НЕПРЕРЫВНОГО ДЕЙСТВИЯ
Точечный источник непрерывного действия
Возьмем бесконечно большое теплопроводящее тело и в его точке о, с которой совместим начало координат, в момент t = О поместим точечный источник интенсивности q, действующий непрерывно в промежутке времени 0 «£ т С t. Обозначим его интенсивность в промежуточный момент т через q (т). Температурное поле точечного источника непрерывного действия можно получить наложением полей элементарных мгновенных источников, заполняющих интервал (0, /). Действительно, температурное поле мгновенного точечного источника с теплосодержанием dQ = — q (т) dr, помещенного в точке п в момент т, определится по формуле (2.3), если туда вместо t подставить время действия этого источника (/ — т). Суммируя температурные поля всех таких элементарных источников, вносимых в точку о за период от т = О до т = t, получим температурное поле точечного источника непрерывного действия:
|
3/2 |
Т (R t) = [______ <7 (т) dx п 4a (t—т)
J r. v Г4.ТТа (і — 1
су [4яа (t — т)]'
Для источника постоянной интенсивности будем иметь:
т^ = -^Ьггт<<2J>
Введя новую переменную
11 = 4a (t — т) ’ (2'8)
где при изменении т в пределах от 0 до t переменная ц изменяется в интервале
R2
|
(2.9) |
получим
4>.я3/2 R J V-n
3L
4 at
R2
Вместо того чтобы интегрировать отдо оо, можем интегриро-
R2
вать от - щ до нуля, а затем от 0 до оо. При этом получим
Первый из этих несобственных интегралов равен У л, а второй
равен
|
|
|
Таким образом, окончательно имеем |
где функция Ф называется интегралом вероятности Гаусса [102], который может быть представлен также в виде сходящегося бесконечного ряда
|
|
(2.10)
(2.11)
Этот результат позволяет сделать следующие выводы:
а) температура в самом источнике бесконечна и вместе с удалением от него быстро падает в начальный момент процесса нагрева;
б) вместе с возрастанием времени действия источника кривые Т (R) становятся более пологими, приближаясь в пределе при t = оо к гиперболе
|
|
и, следовательно, температурное поле при длительном действии источника постоянной интенсивности стремится к предельному стационарному состоянию.
Температурное поле точечного источника в бесконечном теплопроводящем теле можно использовать для изучения температурного поля, возникающего при сварке толстых пластин. При достаточно большой толщине пластины ее можно рассматривать как полубесконечное теплопроводящее тело. Совместим координатную плоскость хоу с граничной плоскостью полубесконеч - ного теплопроводящего тела, которую будем считать теплонепроницаемой.
Если в начале координат поместим точечный источник с интенсивностью q, то температурное поле, вызываемое этим источником в этом полубесконечном теле, можно рассматривать как часть температурного поля в бесконечном теплопроводящем теле при условии, что не будут нарушены условия на граничной плоскости. Для этого достаточно полубесконечное тело продолжить в направлении г<0ив соответствующей точке о плоскости z = — —0 поместить источник такой же интенсивности q. Тогда граничные условия не будут нарушены и температурное поле в полубесконечном теле с точечным источником с интенсивностью q на теплонепроницаемой граничной плоскости z = 0 будет являться частью температурного поля в бесконечном теле с точечным ИСТОЧНИКОМ удвоенной МОЩНОСТИ 2(7 в плоскости 2 = 0.
Линейный источник непрерывного действия
Аналогично предыдущему, температурное поле линейного источника непрерывного действия С интенсивностью <7! (т) в момент времени t можно найти суммированием температурных полей мгновенных линейных источников, заполняющих весь промежуток времени (0, і). При этом в соответствии с формулой (2.5) получим:
і г2
|
Т(г.0 = J |
?1 СО dt _ Ла (/ х) 4nk(t — т)
В случае линейного источника постоянной интенсивности qt будем иметь:
(2|2>
о
Если ввести новую переменную
— г2
^ 4а (/ — т) *
то (2.12) примет вид
= & Ї (2.13)
гя
4at
Имея в виду, что
j -^rdu = Ei(u)
л конечном виде не берется [102], называется интегрально показательной функцией, в нашем случае получим
4
В соответствии с этим (2.13) примет вид
[-£,(—£)]• <2Л4>
I С ЛII иметь в виду, что
гг
Е, (- и) = е-“ 2 (- l)ft + Я». (2-15)
ія«і<—гг~^;
1U I” '1 cos JL 1 1 2
U = Ue^;
Ф2 < я2,
то ясно, что при длительном действии линейного источника постоянной мощности qx температура па конечных расстояниях стремится к бесконечно большим значениям, а температурное поле стремится к плоскорадиальному полю линейного источника и удовлетворяет уравнению Лапласа для двумерной области с осевой симметрией
ЛГ=-Г1г('-^) = 0- <216>
|
Т (г, оо) = С ■ - - kzt In г, (2.17) |
Решением этого уравнения будет
2 пк
которое и определяет предельное температурное состояние.
Температурное поле линейного источника используется для изучения температурных полей, возникающих при сварке тонких пластин. Если из теплопроводящего тела вырезать пластину малой толщины h двумя плоскостями, нормальными к оси г, и в его элемент hdxdy в момент t = 0 ввести Q калорий тепла, то источник с интенсивностью
„ __ dQi __ 1 dQ /п 1 q-j
У1 ~йГ ~ ~h ~df (2Л8>
создаст температурное поле по (2.14) при условии, что граничные
h
плоскости z = ± - g - пластины непроницаемы для тепла.
Плоский источник непрерывного действия
Если плоский источник с интенсивностью q2 действует непрерывно в течение промежутка времени (0, і), то создаваемое им температурное поле, аналогично предыдущему, можно найти суммированием температурных полей плоских источников мгновенного действия С интенсивностью <72 (т)> заполняющих весь промежуток (0, t). В соответствии с (2.6) будем иметь
Т (.х, О = [ —q;(т) d - е~ 40 (<-т) (2.19)
J су V4яа (t — т)
В случае источника постоянной мощности получим
t _
Т (х, і) = Ц=- f (t — ту-We ^40 (<~т) йх, (2.20)
су у 4тса g
т. е. температурное поле плоского источника непрерывного действия с постоянной интенсивностью в пределе при t —> оо стремится к стационарному линейному полю, удовлетворяющему уравнению Лапласа для одномерной задачи
^ = 0, (2.21)
решением которого будет
|
(2.22) |
Т(х, оо) = С-^х.
Температурное поле, создаваемое плоским источником непрерывного действия, используется при изучении температурных полей, возникающих при сварке встык тонких стержней и узких полос.