СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ

ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ СВОБОДНОЙ ПОЛОСЫ, ВОЗНИКАЮЩИЕ В РЕЗУЛЬТАТЕ НАЛОЖЕНИЯ ВАЛИКА НА ОДНУ ИЗ ЕЕ ПРОДОЛЬНЫХ КРОМОК

Теоретическое решение

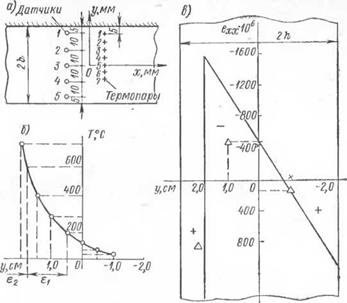
Упругое состояние полосы. Возьмем тонкую свободную по­лоску толщиной h, шириной 26. Начало координат поместим в центре тяжести среднего по длине поперечного сечения полосы (рис. 27, а). Найдем деформации и напряжения этой полосы, воз­никающие в результате наплавки валика на ее продольную кромку. Ширину изотермы Тк предельного состояния нагрева обозначим через є2, расстояние между огибающей изотермы Тк и изотер­мой Ту этого состояния по нормали к изотерме Тк и к ее огибаю­щей — через Ej. Пусть ах — расстояние от оси полосы до изо­термы Ту по этой нормали. К решению этой задачи применим пер­вый метод (п. 29) и используем первый способ уточнения (п. 31). В предельном состоянии нагрева, если не учитывать влияние не - одновременности остывания, распределение пластических дефор­маций нагрева по ширине полосы согласно основной гипотезе и первому способу уточнения представится соотношениями:

е[р) — 0; -—

eip) — аТк = а(Тк — Тоу, а + Єї =sg г/sg b.

В соответствии с первым методом (п. 29) закон распределения тем пературы охлаждения определится соотношениями:

T = Т<г) = 0; —6 sg // sg Gj;

T = TW = —— y); ei;

T = 71<3) = —TK; a - j - Ei sg у b.

Таким образом, задача сведена к температурной задаче дефор­мируемого тела. В зависимости от величины параметра Тк полоса после мгновенного охлаждения по указанному закону может ока­заться как в упругом, так и в упруго-пластическом деформиро­ванном состоянии. Рассмотрим сначала случай ее упругого состоя­ния. Здесь имеется плоское напряженное состояние (п. 17) и за­дача определения деформаций и напряжений в этом случае сво­дится к определению бигармонической функции ф и функции Тг, удовлетворяющей уравнению Пуассона

у2Тj = аЕТ.

Так как в нашем случае температура Т зависит лишь от у, то урав­нение (8.2) дает

(8.4)

Взяв функцию ф в форме

Ф = СіУ3 + СгУ2

и имея в виду (8.4), для напряжений (8.3) получим:

охх = 6 Сху + 2С2 — аЕТ;

(а)

где постоянные С і и С2 определяются из условий равновесия внутренних сил:

J oxxdF = 0

F

| °xxydF = 0.

F

Если учесть (8.1), (а), последние дадут:

При этом для нормального напряжения охх по первой из фор­мул (а) получим:

о(хх = —аЕТ'к ~~~ - ф аїї;

(і)

о{хх — аЕТк + о. Деформации найдутся по формулам:

М)

аТ, п;

(8.8)

Смещения определятся из уравнений Коши:

ди ___ оХх і Г, Т-

дх ~ Е ■ ’

дії Ц f гтч

~ду — Е~ хх + a ’

dv. ди п дх ' ду ’

интегрирование которых, если отбросить не влияющие на отно­сительные деформации члены, дает

при принятых условиях дает

откуда

где а0 и bо — постоянные интегрирования.

Для определения постоянных Сг, С2, а0, Ь0 и величины г имеем условия:

f охх dF = 0; J cxxydF = 0;

ф(т)) = 1; l)y) (т]) = у(Р) (ц).

Первые два из этих условий дадут:

_ аЕТк (T1_fll)a(3b + 2al + i1) 2a>(6-rj)

1_ бвх (Ь+Ч)3 (6 + Т1)3

аЕТ' _

(8.16)

2ех с' (6 —Т])

[ЗЬ2 + (2Ь —ц)2].

2(6 + т])3

Третье из уравнений (8.15) вместе с четвертым дает 6СіТ) - ф 2С2 — а£Т (т)) = - g - (1 - ф р)

откуда, имея в виду (8.16), получим уравнение

[і з - (1 + р)] т12 +1 е J Ф + ai)2 b (1 - ф р) — о] j1! —

г о ~i аЕТ

-ъ% [7 + - г(1 + ai {Ъ+Gl)2 = °- (8Л7)

Определив из последнего уравнения величину "г), по форму­лам (8.16) можно найти значения постоянных Сх и С2.

Смещения ииввупругой зоне, имея в виду (8.11), можно найти интегрированием уравнений Коши. Отбрасывая члены, не влияю­щие на относительные деформации, получим:

и = - jr (ЄСіу - ф 2С2) X] хР' = -±(ЗС# + 2С1у + а(1+р)Т<1у-*££-. j

Аналогичным образом, используя соотношения (8.12)—(8.14), можно найти смещения и(р), v{p) в пластической области.

Если принять, что металл зоны интенсивного нагрева после остывания следует схеме идеальной текучести, то нет необходи­мости в определении uiP), Vі-р), так как общее изменение формы полосы после наплавки и остывания определится изменением формы ее упруго-деформированной части при найденном г).

Наибольший практический интерес представляет случай, когда ширина зоны интенсивного нагрева мала по сравнению с общей шириной полосы. В этом случае, в зависимости от степени жест­кости полосы, могут иметь место значительные пластические де­формации нагрева в зоне, где в предельном состоянии нагрева Т <: < Тк. Эти пластические деформации должны быть учтены в соот­ветствии с первым или вторым способами уточнения (п. 31) на­равне с главной частью а (Тк — 7’0) активных пластических де­формаций нагрева, определяемой основной гипотезой.

Если полоса имеет такую незначительную ширину, что ширина зоны интенсивного нагрева сравнима с ее общей шириной, то ввиду малой жесткости такой полосы, ее деформации (напряжения) после наплавки валика и остывания определятся главным образом актив­ной пластической деформацией нагрева зоны, где в предельном состоянии нагрева Т ^ Тк, а пластическими деформациями на­грева зоны, где Т Тк, можно пренебречь. При этом распределе­ние температуры мгновенного охлаждения представится соот­ношениями:

71(1) = 0; —b^y^cii,

Т^=-Т'к-, а^у^Ь.

Предполагая, что полоса остается в упругом состоянии, по­лучим:

aET'Kh(b2-a)_

6С* =---------------- 2Гг------- ’

aET'Kh(b-ai)

2 — р >

охх = 6 Сгу - ф 2 С2 — аЕТ; (8-19)

п(1) = п(2) = - L (6 Сгу + 2С2)х;

v(1) = v(2) = - - Ф - (3 СгУ2 + 2 С2у) --ф сс (1 + p)J Т dy.

Если предположим, что металл зоны интенсивного нагрева после остывания имеет средний предел текучести as и следует схеме иде­альной текучести, то приближенно можно принять, что вся зона «і «S у ^ b целиком переходит в пластическое состояние при том же значении аТк параметра аТк, при котором напряжение

в точке у — впервые достигает значения предела теку­

чести os, т. е. Тк найдется из условия

(8.20)

При этом напряжения в пластической зоне будут равны os, а в уп­ругой зоне деформации и напряжения определятся формулами (8.19), где вместо аТк необходимо подставить аТк. Смещения ы(1), при том же значении аТк основного параметра будут опре­делять общее деформированное состояние полосы.

Таким образом, мы видим, что эта классическая задача теории сварочных деформаций и напряжений может быть решена при­ближенно до конца аналитически. При этом полученные здесь выражения для деформаций, смещений и напряжений могут быть использованы для любой заданной свободной полосы с любым за­данным режимом сварки, характеризуемым параметрами е2, ex.

Опытная проверка

Опытная проверка изложенных выше результатов проводилась на образцах-полосках 11, 12, 13, 14, первый из которых имел размеры 600 X 50 X 7 мм, второй и третий — 1170 X 100 X X 7 мм, а четвертый — 1170 X 170 X 7 мм. Они были изготов­лены из стали типа CXJT. На одну из продольных кромок каждого из них наплавлялся валик при постоянном режиме сварки. Схема установки термопар приведена на рис. 27, а. Во всех случаях замеры температуры производились путем одновременных отсче­тов по семи гальванометрам. Температурная кривая предельного состояния нагрева для образца 11 приведена на рис. 27, б. Замеры деформаций во всех случаях производились методом, изложенным в п. 28. Датчики к образцам приклеивались после наплавки валика и последующего остывания с двух сторон листа и были соответ­ственно обозначены: 1—5; Г—5'. Схема приклейки датчиков к об­разцу 11 приведена на рис. 27, а. После приклейки и сушки по­казания датчиков контролировались до тех пор, пока они не станут стационарными. Датчики 3, 5, V, 2', 5' не дали показания после вырезки из-за повреждения при вырезке. Показания всех осталь­ных датчиков образца 11 как до, так и после вырезки, приведены ниже в табл. 12, где Р — реахорда, Д — диапазон. Там же даны значения продольных относительных деформаций этой полосы, которые нанесены на рис. 27, в значками Д, X. Для этого образца зона нагрева до Т ^>ТК при Тк = 600° С без учета толщины на­плавленного металла имеет ширину «^0,59 см. Средняя толщина наплавленного металла оказалась равной 1 мм. Таким образом, зона нагрева до Т ^ Тк имеет ширину є2 = 0,69 см. Тогда, имея в виду, что 2ft = 5,1 см, а1 = b — = 1,86 см, а средний для
зоны интенсивного нагрева предел текучести as = 4700 кГ/см2, по формуле (8.20) получим

с. = 0,561 аЕТк

откуда

Тк = 335° С.

Для постоянных Сх и С2 из формул (8.19) получим:

6СХ = —1150;

2 С 2 = —1130.

Зная Сг и С2, можно определить напряжения ахх и деформации упругой зоны (табл. 12).

На рис. 27, в приведен график теоретических значений ехх, полученных этим приближенным методом. Сравнение опытных и

теоретических значений ехх

указывает на их удовле­творительное соответствие. Таким образом, в случае, когда ширина зоны наг­рева до Т^ТК сравнима с общей шириной полосы и зона нагрева охваты­вает всю ее ширину, ос­новная гипотеза дает удовлетворительные коли­чественные результаты и в силу малой жесткости полосы пластические де­формации нагрева зоны, где Т < Тк, будут незна­чительными и их можно не учитывать.

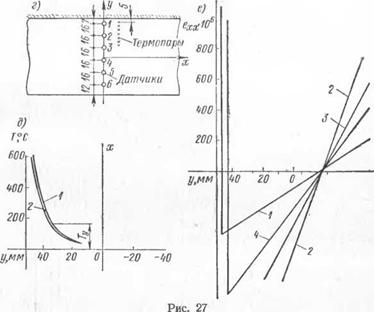
В случае более жесткой полосы, когда ширина зоны нагрева до Т > Тк составляет лишь малую долю ее общей ширины, а ши­рина температурного поля предельного состояния нагрева меньше ширины полосы, пластические деформации нагрева зоны, где Т sg: Тк, будут значительными и их надо учитывать. Для подтвер­ждения этого положения приведем результаты опытов с образ­цами 12 и 13. Схема установки термопар и приклейки датчиков приведена на рис. 27, г, а на рис. 27, д приведены температурные кривые предельного состояния нагрева образцов 12 и 13 (/, 2). Опытные значения продольных деформаций с обеих сторон образ­цов даны в табл. 13 и нанесены соответствующими значками на рис. 27, •, о — образец 12; X, Д—образец 13. В данном

случае при толщине наплавленного металла в 1 мм для ширины зоны нагрева до Т ^ 600° С (рис. 27, д) имеем е2 = 0,4 см. Тогда, имея Ь = 5,05 см, cs = 4700 кГ/смг, а = 12,5• 10_е, из соотно­

си

шений (8.19), (8.20) получим Тк = 221° С. При этом для относи­тельных деформаций упругой зоны по формулам (8.19) будем иметь: ехх (0) = 108-10 6, ехх (—Ь) = 207 • 10 ~6. Эпюра этих относи­тельных деформаций приведена на рис. 27, е (прямая /). Основная гипотеза в данном случае дает лишь качественную картину. Для получения удовлетворительных количественных результатов должны быть учтены пластические деформации нагрева зоны, где Т <1 Тк. Сначала используем первый способ уточнения (п. 31). Имея Ь = 5,05 см, е2 = 0,4 см, ej = 1,05 см (рис. 27, д), получим Й! = 3,5 см. При Е = 2-106 кГІсм2, р. = 0,3, os = 4700 кГ/см2 соотношения (8.17), (8.16) дадут: т] = 4,0 см, 6Сх = —530, 2С2 = = —984. Для относительных деформаций упругой зоны по фор­мулам (8.11) получим: ехх (0) — —492-10-6, ехх (—b) = 843-10-® (рис. 27, е, прямая 2). Отсюда ясно, что первый способ уточнения дает несколько завышенные по сравнению с опытными значения деформаций.

Используем теперь упрощенный первый способ уточнения, т. е. примем, что вся зона, где в предельном состоянии нагрева Т I т

Т Тс = ■ у, получила активную пластическую деформа­цию нагрева а (Тк — Т0). Ширина этой зоны с учетом толщины наплавленного металла (рис. 27, д) равна є2 = 1,0 см. При этом

формулы (8.19), (8.20) дадут: Тк = 275° С, ехх (0) = —330 X X 10 _6, ехх (—Ь) = 580-10_6. Отсюда ясно, что этот упрощенный способ уточнения дает (рис. 27, е, прямая 3) вполне удовлетвори­тельные количественные результаты.

Используем далее второй способ уточнения. Исследование микротвердости основного металла зоны шва показало, что она вместе с удалением от оси шва постепенно уменьшается и дости­гает своего нормального значения на расстоянии 6,5 мм от кромки. Если учесть толщину наплавленного металла, то в соответствии

со вторым способом уточнения получим, что зона шириной е2 = = 0,75 см в предельном состоянии нагрева получила активную пластическую деформацию а (Тк — Т0). При Ь = 5,05 см, ах = = 4,3 см формулы (8.19) и (8.20) дадут: Тк = 256° С, ехх (0) = = —238- Ю"6, ехх (—Ь) = 422-10 ®. Отсюда ясно, что второй спо­соб уточнения также дает удовлетворительные количественные результаты (рис. 27, е, прямая 4).

Таким образом, как упрощенный первый способ уточнения, так и второй способ уточнения позволяют получить удовлетвори­тельные значения сварочных деформаций и напряжений, причем теоретические значения деформаций, полученные путем исполь­зования второго способа, оказываются незначительно занижен­ными по сравнению с их опытными значениями. В дальнейшем будем пользоваться как первым, так и вторым из этих двух спо­собов уточнения.

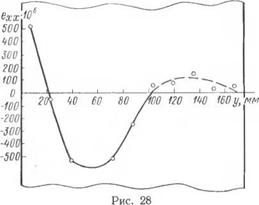
Для образцов 11, 12, 13, имеющих соответственно Ц2Ь = 12, 112Ъ =11,7 (2b — ширина пластины), как показывают приведен­ные выше результаты опытов (рис. 27, в, е), гипотеза плоских сече­ний сохраняет силу. При уменьшении отношения 112b гипотеза плоских сечений теряет силу, что подтверждается рис. 28, где приведена кривая опытных значений продольных деформаций об­разца 14, для которого 112b 6,9.