Сварные конструкции. Расчет и проектирование
ОПРЕДЕЛЕНИЕ УСИЛИЙ СТЕРЖНЕЙ ФЕРМЫ АНАЛИТИЧЕСКИМ МЕТОДОМ
Усилия стержней фермы определяются по правилу РОЗУ: разрез фермы; отбрасывание одной части; замена стержней силами; условия равновесия отрезанной части.
Разрезы производят методами вырезания узла и рассечения фермы. В месте разреза к стержням прикладывают неизвестные силы и направляют стрелки от сечений. Растягивающие усилия считают положительными. Допустим,
что после решения уравнений статики искомое неизвестное усилие имеет отрицательный знак. Эго указывает на то, что знак усилия первоначально был выбран неправильно. Стержень оказывается не растянутым, а сжатым.
|
стержнях фермы меюдом вырезания углов (перечеркнутые стержни не испытывают усилий) |
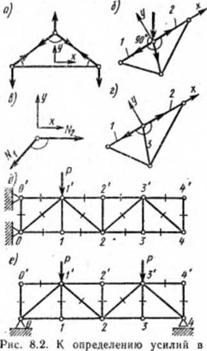
Определение усилий в стержнях ферм методом вырезания узлов удобно в следующих случаях: 1) в узле сходятся два стержня (рнс. 8.2, а), при этом усилия находят нз уравнений VX-0, 0; 2) в
узле сходятся три стержня, два из них являются продолжением один другого (рнс. 8.2, б), усилие в третьем стержне определяют проектированием всех сил на направление, перпендикулярное х; 3) в узле сходятся несколько стержней, при этом все усилия, кроме двух, уже найдены какими-либо другими приемами.
Нели в узле сходятся два стержня и отсутствуют внешние нагрузки, то усилия в обоих стержнях равны нулю. Спроецируем все силы на вертикаль откуда
Л=0 (рис. 8.2, в), из условия.2*=° следует, что /V,—0.
Если в узле сходятся три стержня при условии, что два являются продолжением одни другого (рис. 8.2, г) и в узле отсутствует внешняя нагрузка, то усилие в третьем стержне равно 0. Проецируем силы на направление у, перпендикулярное стержням / и 2,
Убеждаемся в правильности того, что продольное усилие в третьем стержне jV»=0.
Легко показать, что в системе, изображенной на рис.
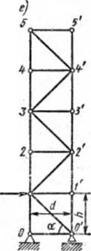
8.2, д, усилия во всех стержнях, кроме ОТ и 0Ґ, равны
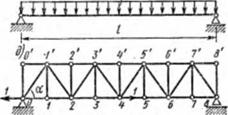
нулю, рассмотрите равновесие узлов 4', 4, 3, 3' и т. д., а в системе на рис. 8.2, е усилия в стержнях 00', 11', 22', 33', 44', O’!', 3'4‘, Ґ2, 23' равны нулю при заданных условиях нагружения.
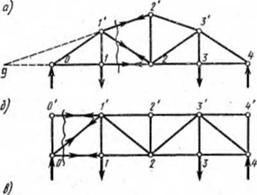
При определении усилий в стержнях фермы методом ее рассечения (рис. 8.3, а) необходимо составить уравнения равновесия в виде
2М, = 0; УМг = 0; = (8.3)
где /', 2 и g — момеитные точки.
|
|
|
Рис. 8.3. К определению усилий н стержнях методом рассечения ферм: и — ферма с непараллельными поясами; 6, в — фермы с параллельными поясами |
Точки называют моментными, если они определяются пересечением двух из перерезанных стержней фермы.
Моментная точка /' лежит на пересечении стержней 1'2‘ и 1'2; точка 2 — на пересечении 1'2 и 12; точка g — на пересечении 12 и /'2'.
Если рассматриваемые разрезанные стержни параллельны, например стержень 0! и O'1' (рис. 8.3,6), то моментная точка g перемещается в бесконечность. При этом
статические уравнения равновесия следует написать в форме
2Л1, = 0; 2^1 = °: 2У' = °* (8-4)
Каждое уравнение содержит одно неизвестное, так как остальные неизвестные усилия образуют относительно моментной точки моменты, равные нулю.
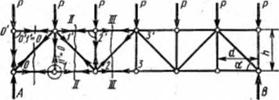
Определим усилия в стержнях фермы (рис. 8.3, в) с параллельными поясами.
Вследствие симметрии фермы и нагрузки опорные реакции равны между собой:
А = В = 3,5Р.
Разрезаем третью панель фермы (разрез III—III). Пишем условие равновесия отрезанной левой части фермы, нагруженной реакцией Л, силами Р и усилиями стержней 7 3', 23 и 23' в виде 2^т'=^;
3,5P-3d-P3d-P2d-Pd-23h = 0, (8.5)
откуда
М = 4,5^, (8.6)
где Mt— момент сил, расположенных слева от разреза, относительно точки У при учете фермы как сплошной балочной системы
Напишем условие ^Мх=0:
TOC o "1-5" h z 3,bP'2d-P2d-Pd+2,3'h = 0; (8.7)
2'3'------- -¥г = — «j, (8.8)
где М| — момент сил, находящихся слева от разреза относительно точки 2.
Напишем условие 2^=^:
3,5/> — Р—Р—Р + 23' sina = 0; (8.9)
23' = -^iiL = 0,5 , (8.10)
sin a ’ stua ’ ' '
где Q,,, — поперечная сила от сил, расположенных слева от разреза при рассмотрении фермы как сплошной балочной системы.
Производим подобные разрезы по второй и первой панелям.
Подобным же образом находим усилия в остальаых стержнях поясов и раскосов.
Усилия в стойках находим методом вырезания узлов. Вырезаем узел 0'. Тогда
откуда
0'0 = — Р. (8.12)
Вырезаем узел /. В этом узле нет сил, поэтому из условия 2К=0 находим 11'=0.
Вырезаем узел 2'. При этом имеем
'£Y = — 22'-P = 0, (8.13)
откуда
22' = — Р. (8.14)
Легко показать, что распределение усилий в стержнях поясов сквозных ферм с параллельными поясами подобно распределению изгибающих моментов в балочных сплошных конструкциях. Нижние пояса растянуты, верхние сжаты при нагрузках, изображенных на рис. 8.3, в. Усилия в стержнях поясов возрастают от опор к середине
пролета.
Распределение усилий в раскосах сквозных ферм с параллельными поясами подобно распределению поперечной силы в балочной сплошной конструкции. Усилия в раскосах имеют наименьшую величину в середине пролета. Усилия возрастают от середины пролета фермы к ее опорам.
Перемещения узлов фермы от вертикальных нагрузок
определяют по формуле Мора:
|
ЕА |
(8.16)
где N — усилие в стержнях фермы от заданной нагрузки; NI — усилие в стержнях от единичной силы, приложенной
|
|
|
t/г р 1 |
|
|
|
/} |
|
EEfflZSZS |
|
|
|
о і г з ч № $ л |
|
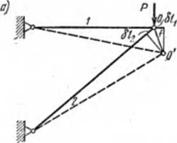
Рнс. В.4. Определение перемещений узлов ферм под нагрузкой: а — перемещение узла О л плоскости; О — к определению усилий » стер кии* фермы от нагрузки Р; * — от единичной силы в узле 4’; а — я а зкпкиалентипП балке; 0 — от горизонтальной единичной силы в узле 4; • — к определению усилий в вертикальной ферме |
|
р Г • |
р Ґ ' |
Р Г |
р Ґ ' |
р |
Г I |
р |
р |
|
|
fa |
/ |
с |
||||||
|
0 |
1 2 J ♦ |
а |
4/ |
|
Є' /' /' Ґ *4 |
|
Ь) |
в узле, в котором определяется перемещение по направленню искомого перемещения; 1( — длина /-го стержня; А — площадь его поперечного сечения; Е — моду г. упругости.
ПРИМЕРЫ РАСЧЕТА
Пример 1. Рассмотрим пример определения вертикального перемещения (прогиба) среднего ума фермы, изображенного на рис. 8.4, б. Примем, что площади сечений элементов поясов одинаковы и равны Лп; площади сечений раскосов и стоек также одинаковы и равны /4р, Расчет удобно расположить в форіе табл. 8.1. Так как система и нагрузка в ней симметричны, усилия следует вычислять лишь для одной половины фермы.
На рнс. 8.4, в изображена та же ферма пол действием единичной силы, приложенной в среднем узле вертикально. Пользуясь методом РОЗУ, вычисляем усилия N в стержнях фермы от сил Р, усилия JVt в аналогичных стержнях от силы, равной единице. Реакция от нагрузок А~£=4,5 Г: реакция от единичной силы: А — = £=0,5
У Л/ЛУ, 54р<р 4.5РЛ
ЕА h? EAB £/4рsln*a' 1 '
Вертикальное перемещение среднего узла фермы равно удвоенному значению суммы, определенной с учетом деформаций одной половины фермы. Таким образом,
|
Ла£Л„ + £Л„ sin3a ‘ (8 16) |
108Pd* . 9 Ph
In £і4р5
Первый член суммы — это величина прогиба, определяемого деформациями поясов, а, второй член — величина прогиба, определяемого деформацией решетки. Как видно из приведенного соотношения (8.18), деформации фермы зависят в очень большой степени от площадей сечений поясов и решетки.
Допустим, что (в частном случае) все площади сечений элементов равны между собой A„—Af— А, тогда
, ( 108Pd3 , 9Ph 1
'-[-Г+ІйРЇГІ-їїл - <8Л9>
Очевидно, что влияние деформации поясов на прогиб в этом случае более значительно, нежели влияние деформации решетки. р
Обозначив ~ — <1 и поле гаинн в формулу (8.19), получим
TOC o "1-5" h z, ( I08pd* , 9Ph 1
{ IIі 1 sin»» ) F. A '
Приближенно примем, что 2А„ j = J, т. е. моменту инер
ции поиеречиого сечения фермы, и d—//8. тогда
108<?/4 I gl* , 94dU
1 mbtJ sin» а ЕА — 75 EJ 1 sin3a£/l •
|
Таблица 8.1 Определение вертикального перемещения
|
|
01 |
3,5Pd/h |
0,5d/h |
1,751T |
|
|
12 |
3,5Pd/h |
0.М/Л |
||
|
23 |
7,bPd/h |
l,5d/h |
Pd3 11.25-^ |
|
|
34 |
T. bPdjh |
1,5d/h |
d |
Pd3 ii.*t |
|
04' |
0 |
0 |
0 |
|
|
vr |
-6 Pd/h |
— 1 d/h |
||
|
2 '3' |
—GPdih |
—d/h |
||
|
3‘4' |
—6Pd/h |
—2djh |
bPd% 161T |
|
|
01' |
—3,5P/slna |
—0,5 l/віл a ' |
1,75-^- sin3 a |
|
|
1'2 |
+2,5P/sln a |
+0,5 1/sln a |
h |
|
|
23' |
—l,5P/sln a |
—0,5 1/sln a |
sin a |
0,75 sin* a |
|
34 |
+0,5P/slna |
+0,5 1/sln a |
0,25 —py— sin* a |
|
|
00' |
— P |
0 |
0 |
|
|
IV |
0 |
0 |
h |
0 |
|
2Ї |
— P |
0 |
0 |
|
|
33' |
0 |
0 |
0 |
|
|
44' |
— P |
-1 |
h/2 |
0.5РЛ |
|
Длина средней стойки при суммировании деформаций элементов одной половины фермы принимается равной 0,5А |
Интересно отметить, что прогиб сплошной балки (рнс. 8.4, г) от равномерно распределенной нагрузки составляет
. 5 qP____ 1 д Iі
384 EJ “77 EJ ‘
Таким образом, вертикальная составляющая прогиба фермы от сил Р, вызванная деформациями поясов, близка по величине прогибу от равномерно распределенной нагрузки q в балке силошного сечения,
Если принять а=45°, т. е. ft=d и sina=0,7, то соотношение (8.19) примет вид
/=(108Pd -|- 23Pd) ~р. (8.?1)
Таким образом, деформация решетки увеличивает прогиб, вызванный деформацией поясов, на 20%. Эта цифра верна в предположении, что 4п=у4р, если /4п<4р, что часто бывает, то величина деформации раскосов на прогиб оказывается более значительной.
Пример 2. Рассмотрим в качестве примера определение вертикального перемещения среднего узла фермы 4’, изображенного на рис. 8.4, д, в результате повышения температуры стержней нижнего пояса на /. Коэффициент температурного расширения металла а известен.
В формуле (8.16)
|
УУ,'< ПА |
|
(8.22) |
Л' / ■
величина - jr-j - представляет собой деформацию стержня; в данном
L П
случае она вызвана его нагревом. Обозначим сс blt. Температурные удлинения стержня
Ы, = oil,-. (8.23)
Поэтому формула (8.16) примет вид
f^atliNi. (8.24)
Ответ: f—8atd4h (8.25)
Пример 3. Определим горизонтальное перемещение точки 5'
вертикальной фермы от силы Р, приложенной в узле 1 (рнс. 8.4, с)
ЕА = consl.
Следует обратить внимание, что усилия N от силы Р во псех элементах, кроме 0! и 0'1, равны 0.
Ответ: ^ ( 5ft tg’ a + . (8.26)