СВАРКА разнородных металлов и сплавов

ДИФФУЗИОННЫЕ ПРОЦЕССЫ НА ГРАНИЦЕ КОНТАКТА

Диффузия играет важную роль во многих процессах, протекаю­щих при сварке разнородных металлов. Диффузия вызывает пере­распределение элементов в зоне сварного соединения; с нею связы­вают возникновение микронеоднородности сварных швов.

Диффузионные процессы обусловлены флуктуацией энергии ато­мов и дефектами кристаллической решетки. Движущими силами диф­фузии при сварке в твердом состоянии являются градиент хими­ческого потенциала, концентрации и фактические внутренние напря­жения. Под действием этих напряжений диффузия идет весьма инг - тенсивно, к тому же в процессе ползучести материала возникают дополнительные вакансии. Надежность соединений повышается за счет переходной зоны, которая образуется путем взаимной диф­фузии атомов. Однако в ряде случаев, когда имеет место выделение интерметаллических фаз, механические свойства соединений могут ухудшаться.

К настоящему времени осуществлено много экспериментальных работ по исследованию взаимной диффузии для систем, образующих непрерывный ряд твердых растворов, а также для систем, образую­щих интерметаллические соединения (реактивная диффузия). Уста­новлено [14], что в системах первого типа диффузионный слой характеризуется непрерывным изменением состава диффузионного слоя. В системах второго типа образуются слои интерметаллических соединений, соответствующих диаграмме состояний. Состав и поря­док образования слоев при диффузии определяются диаграммой состояний изучаемой системы. Подробный обзор результатов иссле­дования взаимной диффузии дан в работах [26, 84].

Сварка металлов в твердом состоянии. Для соединения разно­родных металлов в твердой фазе необходимы развитие физического контакта, активация контактных поверхностей и объемное развитие взаимодействия. Последний процесс сопровождается диффузией и может заканчиваться образованием интерметаллических фаз и рекри­сталлизацией. В связи с этим необходимо иметь представление о скорости развития диффузионных процессов. В работе [78] мето­дом локального рентгеноспектрального анализа исследована зона объемного взаимодействия золота с серебром (металлов, образующих непрерывный ряд твердых растворов), полученная сваркой давле­нием с импульсным косвенным нагревом. Золотая прокладка (зо­лото марки Зл 999,9 ГОСТ 6835—80) толщиной ~20 мкм находилась на никелевой ленте, серебряная — толщиной ~50 мкм — на квар­цевой пластине. Никелевую ленту с кварцевой пластиной соединяли через золотую и серебряную прокладки в атмосферных условиях под давлением 60 МПа в течение 0,7 с. Зона контакта золота с сереб­ром при сварке нагревалась за счет теплопередачи от пуансона до температуры 500 °С. После сварки образцы отжигали при 500 °С в течение 1, 5, 10, 30 и 60 мин.

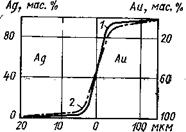
Объемное взаимодействие золота с серебром при импульсной сварке в течение 0,7 с происходит очень интенсивно. За указанное время развивается зона протяженностью до 4,5 мкм. При после­дующем отжиге сварного соединения в течение 10 мин протяженность зоны объемного взаимодействия увеличивается всего лишь на доли микрометра. Распределение золота и серебра в зоне объемного взаимо­действия исследовали методом локального рентгеноспектрального анализа на установке «Камека». На рис. 13 представлены концен­трационные кривые распределения золота в серебре и серебра в зо­лоте в момент окончания сварки при последующем отжиге.

По формуле

с/с0 - 1 —erf (х/2Dt), (13)

где х —расстояние, на котором концентрация равна с D —коэф­фициент диффузии; t —время.

Рассчитаны коэффициенты диффузии золота в серебре [78]. Коэффициент диффузии золота в серебре [26 ]

Dau-as = 5,3- 1(Г4 exp (—29800/ДГ).

При температуре 500 °С DAu-Ag = 2* Ю-1^ см[1]/с. ^

Сравнение коэффициентов диффузии показало, что^в период импульсной сварки коэффициент диффузии золота примерно на четыре порядка больше, чем в случае обычного отжига. Такое суще­ственное увеличение его в серебре можно объяснить тем, что в ука­занных условиях свариваемые металлы подвергаются интенсивной пластической деформации.

При сварке давлением с подогревом наиболее интенсивно пласти­ческая деформация протекает по периферии контактной поверх­ности [77 ]. На краях контактной поверхности коэффициенты диф­фузии золота в серебре в 1,5—2 раза больше, чем по оси сварного соединения.

Рассмотрим механизм и кинетику образования и роста интер­металлических фаз при сварке металлов без расплавления, т. е. типичных реакций в твердом состоянии. В простейшем случае взаимо­действия металла А с металлом В на границе раздела возникает лишь одна интерметаллическая фаза АтВп.

При обсуждении механизма подобного процесса обычно противо­поставляют две точки зрения. Согласно первой —интерметалли­ческая фаза может возникнуть лишь после достижения в погранич­ном слое металла-растворителя предела насыщения твердого рас­твора при данной температуре

А + в'ЛАВ^ААвВ^ААвАтВпВ,

т. е. новая фаза возникает в результате перестройки кристаллической решетки вследствие достижения предела растворимости в погранич­ной прослойке одного из металлов.

Согласно второй —при соприкосновении двух металлов неза­висимо от явления взаимной растворимости может произойти хими­ческая реакция с образованием интерметаллического соединения непосредственно на границе раздела реагирующих металлов

А + В —> Л | Б —> Л | АтВп | В.

Предварительным этапом перед образованием на поверхности сопри­косновения двух металлов новой интерметаллической фазы является

Рис. із. Взаимная диффузия золота и серебра:

I — сварной образец золота с литым серебром;

‘ — сварной образец, отожженный при 500 °С в течение 60 мин

хемосорбция (х. с.), т. е. такая адсорбция, при которой прояв­ляются химические силы взаимодействия. Дальнейший рост интер­металлической прослойки, разделяющей оба металла, происходит за счет диффузионного поступления по крайней мере одного из компонентов к поверхности раздела.

Известно, что в случае постоянства концентрации диффундирую­щего компонента можно получить параболический закон роста слоя

у2 = 2А cDtla = kt, (14)

где у —толщина слоя; Дс —разность концентрации на его грани­

цах; D — коэффициент диффузии в слое; t ■— время; а — некоторая постоянная величина с размерностью концентрации.

Температурная зависимость скорости роста имеет экспонен­циальный характер, т. е.

k = k0 exp (—E/RT), (15)

где E — энергия активации диффузии; k0 — коэффициент, мало зави­

сящий от температуры.

Обе эти зависимости соблюдаются в ряде случаев, но далеко не всегда.

В случае возникновения нескольких интерметаллических фаз картина еще более усложняется (см. рис. 6). Кроме того, в большин­стве случаев свариваются не чистые металлы, а технические много­компонентные сплавы с несовершенной кристаллической структу­рой. Температура и давление в ходе сварки не сохраняются постоян­ными. В целом истинная картина оказывается довольно сложной. При взаимодействии двух твердых металлов действительно возни­кают твердые растворы. Однако интерметаллическая фаза наблю­дается и в случаях, когда твердые растворы еще не достигли пре­дельной концентрации для данной температуры. Интерметаллические фазы образуются также в металле, почти не растворяющем диффун­дирующий компонент, например при диффузии железа в алюминии (предел растворимости <0,025 ат. % Fe при эвтектической темпера­туре и <0,001 ат. % Fe при температурах ниже 500 °С).

Для правильного понимания механизма сварки разнородных металлов и сплавов без расплавления необходимо прежде всего выяснить закономерности ранних этапов диффузионного взаимодей­ствия, когда интерметаллические фазы лишь начинают возникать и их наличие еще не привело к существенному ухудшению механи­ческих свойств. При этом необходимо учесть реальную структуру свариваемых металлов и, в частности, наличие границ зерен, дисло­каций, неравновесных вакансий и др., а также нестационарность по температуре и давлению самого процесса сварки.

Необходимо прежде всего учесть весьма ограниченное приме­нение законов диффузии Фика. Коэффициент диффузии существенно зависит от реальной структуры металлов и от концентрации. Следо­вательно, диффузионный поток будет зависеть от природы и протя­женности границ между зернами, а также от температуры, состава и градиента концентрации. Правда, с повышением температуры эф­

фективный коэффициент диффузии Бьф в поликристалле прибли­жается к значению D, соответствующему достаточно совершенному кристаллу. С другой стороны, в случае D — f (с) две переменные — время t и расстояние у—связаны простым соотношением X =

Это дает возможность получить соотношение

с

Ddc/dk = — (1/2) J Хдс, (16)

Со

где с0—исходная концентрация; с—концентрация, при которой дс/дХ =0 [84].

Аналогичное соотношение получено экспериментально значи­тельно позднее С. Матано, по имени которого и назван метод опре­деления D = / (с). (Плоскость Матано проводят таким образом, чтобы площадь между кривой распределения и осями координат справа и слева от линии раздела была одинаковой.) Метод Ма­тано может быть применен и для анализа экспериментальных ре­зультатов при образовании интерметаллидных прослоек.

При сварке не чистых металлов, а разнородных сплавов диф­фузия может происходить, когда градиент концентрации близок к нулю, при неравенстве нулю градиента термодинамического по­тенциала <5ФІду. Нарушение первоначального распределения угле­рода, возникшее вследствие сварки стали двух сортов различного состава, можно объяснить тем, что сродство углерода к железу больше, чем к кремнию. Подобные явления возрастания градиента концентрации дс/ду в ходе диффузионного отжига сварного стыка не могут быть объяснены в рамках классической теории диффузии. Необходимо - привлечение термодинамических представлений.

Фактическая сила, действующая на диффундирующий атом или ион в бинарном растворе, может быть представлена как отрица­тельный градиент химического потенциала д\,г1ду. Поток атомов i-то сорта

J j as — М іСідФі/dyN ~ — М iCidM t/dy, (17)

где Mi “Подвижность атомов і*го сорта, являющаяся функцией состава при постоянных температуре и давлении. Если учесть связь химического потенциала [А* с коэффициентом активности' yt при постоянном грамм-атомном объеме

{A* as const + RT In УіСі, (18)

то получим следующее выражение для парциального коэффициента гетеродиффузии атомов і-го сорта:

Dt = kTMt (1 + д In уг/д Inc,). - (19)

Впервые эти соотношения были использованы для анализа металли­ческих систем Л. Даркеном. Он установил прежде всего связь коэф­фициентом гетеродиффузии Dt отдельных веществ и соответствую­щих коэффициентов самодиффузии D*. JI. Даркен принял, что под­вижность атомов Afj, определяемая средней скоростью потока при диффузии в случае градиента термодинамического потенциала, рав­ного единице при само - и гетеродиффузии, одинакова для любого вещества. Таким образом, различие между D* и D*t целиком сводится к равным значениям химического потенциала в обоих случаях. При самодиффузии

D* — kTMi* (20)

Из сопоставления (19) и (20) следует

Di = D*£(l+dnyi/dnci). (21)

В частном случае сварки двух разных металлов А и В можно свя­зать коэффициенты самодиффузии DA и Db, определяемые с помощью радиоактивных изотопов, с общшм коэффициентом гетеродиффузии D бинарной системы, определяемым по кривой распределения кон­центрации одного из компонентов в зоне сварного стыка (метод Матано). Согласно соотношению Гиббса—Дюгема для двухкомпо­нентных систем

д In уА/д In сА = д In ув/д In св. (22)

Следовательно, если принять, что состояние микрообъема полностью описывается давлением, температурой и составом, то

D = (NaD*b + NBD) (1 + д In уА/д In сА). (23)

Это выражение позволяет объяснить еще одно явление, наблюдаю­щееся при сварке пар металлов и сплавов, содержащих сильно отли­чающиеся, например по температуре плавления, компоненты. Это так называемый эффект Киркендалла. Сущность его заключается в следующем. Если между свариваемыми пластинами из разных металлов и сплавов поместить инертные метки (например, прово­лочки молибдена или вольфрама или же частицы тугоплавкого окисла), то после нагрева сварного стыка метки сдвигаются в сто­рону пластины, состоящей из вещества с более низкой температурой плавления. Сдвиг меток пропорционален квадратному корню из про* должительности отжига |/7, а скорость сдвига v возрастает с повы­шением температуры. Поскольку это явление связано с различием парциальных коэффициентов гетеродиффузии Dit то согласно (23)

v = (Di — Db) (1 + д In yjd In сА)дсА//ду. (24)

Неравенство парциальных коэффициентов гетеродиффузии приводит не только к смещению сварного стыка относительно первоначальной плоскости соприкосновения, но и к возникновению пор вблизи по­следней со стороны легкоплавкого металла, а также изменению поперечных размеров со стороны тугоплавкого металла.

Эффективный коэффициент диффузии в объеме реального металла отличается от коэффициента диффузии в достаточно совершенном монокристалле того же металла. Эти отличия еще более существенны в микроскопическом масштабе. Поэтому для правильного понима­ния начальных этапов формирования интерметаллидов необходимо учесть, что коэффициенты диффузии у границ зерен Огр и вдоль дислокации D0 существенно превышают коэффициенты объемной диффузии D0q. Так, отношение Drp/Do6 может достигать значения 106 [84]. Поэтому глубина проникновения за счет диффузии по грани­цам зерен и вдоль дислокации больше, чем посредством объемной диффузии, а концентрация диффундирующего компонента окажется повышенной по границам зерен и вдоль дислокаций в зоне сварного стыка по сравнению со средней макроскопической концентрацией на данной глубине у. Этот эффект особенно существен в случае малой предельной растворимости диффундирующего компонента. Тогда перенос вещества (например, железа в алюминий) осуществляется в основном лишь за счет диффузии вдоль дефектов кристаллической решетки.

Возникший локальный объем твердого раствора с повышенной концентрацией может в дальнейшем эволюировать двумя путями: установление упорядоченного расположения атомов в кристалли­ческой решетке твердого раствора; распад последнего на две фазы.

Если энергия связи между двумя атомами различного сорта U АВ больше, чем полусумма энергий связи атомов одного сорта UAB £> ї> (Uaa + Ubb)I2, то в твердом растворе установится упорядо­ченное расположение атомов по узлам кристаллической решетки. Если же, наоборот, UAB < (UAA + UBB)12, то твердый раствор будет распадаться на две фазы. Существует определенная термо­динамическая вероятность локальной флуктуации состава из п-ато­мов растворенного компонента в одном грамм-атоме твердого рас­твора.

Энергия активации, необходимая для такой флуктуации,

TOC o "1-5" h z nW = n[ Ф8-Ф - (x's - х')дФ/дХі], (26)

где Xs и х' — концентрации, выраженные в атомных долях. ,

Начальную скорость выделения можно представить в виде

N exp (-E/RT) exp (nW/RT), (26)

где E — энергия активаций выделяющегося сорта атомов. Время образования первых скоплений

t'o^kз exp [(nW + E)/RT). (27)

Для возникновения интерметаллической фазы необходима еще перестройка кристаллической решетки, т. е. необходимо совершить работу для образования критического зародыша

Ак = aaW2Ap2, (28)

где a — коэффициент формы; а — удельная свободная поверхност­ная энергия зародыша; V — атомный объем; Ар — разность хими­ческих потенциалов в исходной решетке и зародыше.

Скорость^ образования зародышей новой интерметаллической фазы согласно А. Беккеру

N = 64 exp (-E/RT) -exp (-AJRT), (29)

Время образования зародышей новой интерметаллической фазы tQ —ks exp [(Лк - j - Е)/RTJ. (ЗО)

Экспериментальные исследования стареющих сплавов действи­тельно показали, что механизм образования новой фазы довольно сложен. Так, в сплавах системы алюминий—медь при распаде пере­сыщенного твердого раствора меди в алюминии сначала возникают так называемые зоны Гинье—Престона—1, обогащенные атомами меди. Затем происходит частичное упорядочение в расположении атомов (зоны Гинье—Престона—2), и лишь после этого образуется метастабильная 0'-фаза с иной структурой. Равновесная же 0-фаза (СиА12) возникает на поздних стадиях процесса выделения.

Рассмотрим кинетику роста возникших за время t0 центров интер­металлической фазы. Скорость роста кристаллов G определяется выражением

G « G0Gd = aMt (дФJdy)/N, (31)

где G0 —частотный фактор, слабо зависящий от температуры и определяющий максимально возможную скорость роста; GD —диф­фузионный фактор, определяющий концентрацию атомов необхо­димого вида (по составу и энергии) на поверхности растущего кри­сталла; а — геометрический фактор (определяемый формой домена и условиями роста); Mt —подвижность дефицитных атомов в мат­рице; дФі/ду — градиент термодинамического потенциала в направ­лении роста.

Первоначально рост первых кристаллов интерметаллической фазы происходит преимущественно вдоль поверхности раздела обоих металлов вследствие большей скорости диффузии в этой плоскости. После встречи границ первых кристаллов интерметаллидов возни­кает сплошная прослойка, и происходит нормальный рост. Таким образом, зависимость размера у интерметаллической фазы от вре­мени t может быть описана уравнением

уп = k(t — to), (32)

При п = 2 и f > t0 это уравнение переходит в уравнение Там* мана, которое, следовательно, пригодно лишь для описания позд­них стадий роста интерметаллических прослоек.

Экспериментально исследовались ранние стадии процессов обра­зования и роста интерметаллических прослоек в системах ниобий— железо [47], алюминий—медь, алюминий—латунь, алюминий— железо, алюминий—сталь [84].

Анализ микроструктуры зоны сварного стыка в исследованных системах позволяет представить начальные стадии образования и роста интерметаллических фаз следующей схемой: взаимная диффу­зия контактирующих металлов с различной скоростью; возникнове­ние локально пересыщенных твердых растворов вокруг дефектов кристаллического строения; образование первых центров новой фазы в дефектных участках с повышенной концентрацией диффун­дирующего элемента; поперечный рост центров интерметаллической

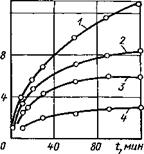
рис. 14. Зависимость толщины слоя интерметаллидов of времени нагрева при температуре, °С:

1 — 1200; 2 — 1100; 3 — 1000; 4 — 900

фазы вдоль плоскости стыка; смыкание и нормальный рост первой сплошной интер­металлической прослойки; образование первых центров второй интерметалличе­ской фазы; продолжение нормального роста первой интерметаллической про­слойки; смыкание центров второй интер­металлической фазы за счет поперечного роста и т. д.

Интерметаллиды на начальных ста­диях развития, когда они не образуют еще сплошного слоя в контакте, практически не оказывают влияния на механические характеристики соединения. При на­личии в контакте сплошного интерметаллического слоя (у ^ 5 мкм) пластичность и прочность соединений начинают быстро падать. Это обусловлено не только высокой хрупкостью новой фазы, но и вну­тренними напряжениями, возникающими вследствие объемных изме­нений.

В конкретных системах имеются свои особенности. В качестве примера рассмотрим закономерности образования и роста интерме­таллического слоя в сварном соединении ниобия с железом [47 ]. Биметалл ниобий (НВ4) — железо характеризуется тем, что ширина переходной зоны (слоя интерметаллидов) не превышает 1 мкм. Толщина указанного слоя у изменяется в зависимости от темпера­туры нагрева (900—1200 °С) и времени отжига соединений (момент появления интерметаллидов фиксировался при уж 1 мкм).

Математические выражения получены обработкой эксперимен - тальйых данных о росте слоя интерметаллидов в зоне соединения ниобия с железом (рис. 14). Зависимость толщины слоя интерметал­лидов от времени нагрева можно описать уравнением

(33)

где у — толщина слоя; t — время отжига; t0 — латентный период, в течение которого интерметаллид вырастает до устойчивого раз­мера; k — параметр, характеризующий скорость роста слоя, опре­деляемый по формуле (15).

С учетом уравнения (15) выражение (33) можно записать

y* = k0e-V*T(t-t0). (34)

Уравнение (34) применимо для практических целей, если известны значения t0^R и Е. Латентный период t0 находят по формуле, учи­тывающей появление интерметаллидов размером меньше 1 мкм:

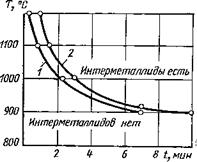
Рис. 15. Зависимость времени появления интерметаллидов от температуры в соедине­нии ниобий— железо:

1 — расчетные данные; 2 — эксперимен-

где коэффициент А не зависит от температуры; Я — эффективная энергия активации процесса об­разования интерметаллида до устойчивого размера.

Для отыскания значений А и Я необходимо построить график

в координатах 1/Т — lg 4- Значения t0 определим из уравнения (33)

= (36)

где ts соответствует величине ys = V УНУ ті Уі и Ут — крайние зна­чения переменной у на рис. 14.

Построение в координатах 1/Т — lg 4 показывает, что имеет место прямолинейная зависимость, которая подтверждает пригод­ность формулы (35) для оценки величин Я и Л. Тангенс угла наклона прямой к оси 1 /Т определяет энергию активации процесса роста интерметаллида, а отрезок отсекаемой прямой на оси ординат, — величину А.

Функция 4 (Т) после отыскания значений Л и Я выражается в виде

4 = 2,5- 10-7е14б>3/дг.

Зависимость времени появления интерметаллидов от температуры, рассчитанная по формуле (36), дана на рис. 15. Логарифмическая зависимость толщины слоя интерметаллидов от времени нагрева до исследуемого диапазона температур выражена прямыми, не прохо­дящими через начало координат и имеющими примерно одинаковый угол наклона к оси lg (t — 4)- Величина lg k для каждой темпера­туры нагрева определяется по отрезку, отсекаемому прямыми на оси ординат. Зная эту величину, путем построения зависимостей lg k — 1/Т легко найти значения Е и k0, а именно: Е = 96,3 кДж/моль, k0 = 6-Ю3 мкм2/мин. Подставив эти значения k0 и Е в выражение

(34) , получим

у2 _ 0. 103е-96,1(/-*о)/ЯГ

Исследовали также структуру переходной, зоны и определяли закономерность образования и роста интерметаллического слоя в зоне контакта ниобия с никелем [55]. Температуру отжига изме­няли от 700 до 1000 °С. Длительность отжига при 700 и 800 °С составляла 10—200 ч, а при 900—1000 °С — 15—180 мин. Переход­ная зона ниобий—никель после отжига характеризуется двумя ти­пами микроструктуры. При температуре отжига до 900 °С эта зона состоит из одного слоя. По данным микрорентгеноспектрального анализа, образуется соединение NbNi и твердый а-раствор на основе никеля. Другой тип микроструктуры переходной зоны наблюдается
при температуре отжига выше 900 °С. В этом случае переходная зона состоит из двух слоев: со стороны ниобия образуется NbNi, затем следует слой NbNi3, за которым располагается область твердого сс-раствора на основе никеля. Рентгеноструктурный анализ поверх­ностей разрушенного образца после отжига при 1000 °С в течение 2 ч показал, что переходная зона содержит интерметаллические фазы NbNi* NbNi3 и Nb5Ni. Микротвердость этой зоны 4000— 4700 МПа. Обработка экспериментальных данных выявила следу­ющие зависимости:

t0 == 7,3 • 10-4е5*85/яг, у2 = 1,54- Юве-143*4<*--*о>/*г,

где t0 —латентный период, в течение которого интерметаллид вы­растает до устойчивого размера (~1,5 мкм).

Взаимодействие твердой и жидкой фаз при сварке. Диффузион­ные процессы на границе между твердым и жидким телом обладают той особенностью, что скорость их определяется интенсивностью диффузии в твердом теле, так как она обычно во много раз меньше скорости диффузии в жидкости.

Процесс взаимодействия твердой и^жидкой металлических фаз при сварке и наплавке сопровождается той или иной степенью раз­вития гетерогенной диффузии в зоне контакта. Составы фаз, нахо­дящихся в контакте, устанавливают в соответствии с требованием равенства их химических потенциалов, и даже незначительное время их сосуществования способствует протеканию процессов гете­рогенной диффузии в направлении установления фазового равнове­сия. Интенсивность протекания этих процессов определяется темпе­ратурой, длительностью контактирования, градиентом концентра­ций и диффузионной подвижностью атомов [105, 123].

С точки зрения развития процессов гетерогенной диффузии на границе раздела фаз определяющей является стадия взаимодействия твердого металла с жидким. Развитие диффузионных процессов на стадии охлаждения закристаллизовавшегося металла в основном определяется временем нахождения металла при повышенных тем­пературах. Для большинства элементов замещения их подвижность при переходе из жидкого состояния в твердое резко падает (коэффи­циенты диффузии уменьшаются на три—пять порядков), и длитель­ность пребывания при повышенных температурах в реальных про­цессах сварки и наплавки оказывается недостаточной для существен­ного развития процесов химической неоднородности.

Одним из основных требований, предъявляемых к соединениям разнородных металлов, является получение соединений с высокими механическими свойствами^ зоне контакта и с минимальным разви­тием процесса растворения твердой фазы, приводящего к переходу элементов основного металла в наплавленный металл. В большинстве случаев как наплавляемый металл, так и подложка являются спла­вами, в связи с этим на свойства получаемых соединений также могут оказывать существенное влияние процессы гетерогенной диф­фузии примесей в зоне контакта.

В литературе имеются многочисленные сведения о влиянии раз­вития процессов химической неоднородности на физико-механические свойства соединений, в частности на механические, коррозионные свойства, на поведение соединений при вибрационных испытаниях и т. д. Количественное решение задачи по гетерогенной диффузии примеси в зоне контакта твердой и жидкой фаз при частных гранич­ных условиях приведено в работах [42, 120, 131]. Характер распре­деления примеси зависит от коэффициента распределения k, харак­теризующего различную растворимость элементов в твердой и жид­кой фазах, от коэффициентов диффузии в твердой DT и жидкой Dm фазах, длительности процесса t и градиента концентрации примеси на границе сплавления.

Условия задачи диффузии примеси в двух средах при частных граничных условиях формулируются следующим образом:

1) dcjdt = DTd2c! dx2, х < 0; dcm! dt — Dmd2c/dx2, х ►> 0;

2) ст = ст0 при / = 0 и х<0; сж = сж0 при t — О и х>0;

3) DT (дст/дх)х==0 = Dm (дсж/дх)х=0 на границе раздела для всех t

0 сю

4) j* (Сто £т) dx = J (сжо сж) dx

—оо 0

5) ст/сж = k в равновесном состоянии.

Решение имеет вид

с™=с'"“^Йг[(1+егГ-5^г)] <37>

где ст (X, о и сж (*, t) — концентрации элемента примеси соответственно в твердой и жидкой фазах в момент і ►> 0 на различ­ных расстояниях х (в см) от границы; сх0 и сж0 — начальные кон­центрации примеси в твердой и жидкой фазах (t = 0 с); DT и Ож — коэффициенты диффузии примеси в твердой и жидкой фазах; k — коэффициент распределения; t —длительность процесса, с.

Если градиент концентраций на границе сплавления при t — 0 отсутствует (наплавка, сварка однородного металла) — с0 = сж = = ст0, уравнения принимают вид

= [l-rf-^)] „p„,>0. (40)

В том случае, если растворимость элемента в твердой и жидкой фазах одинакова (k = 1), возрастает роль градиента концентрации на границе сплавления Дс0 = ст0—ст0:

ІС' Гі+ЄГ'(ірЬ-)] "РИ^<0Г(41)

(x, t) — Ctq

1 _ erf (—

V 21/" Dmt )

В предельном случае, когда DT « Dm (отсутствует граница фаз, температура в металле постоянна), формулы преобразуются в извест­ные уравнения, применяемые для расчета ряда диффузионных про­цессов:

С(х. о = с10 - + erf ( ) при х<0; (43)

Co(x, t) — Сио -[-

Значения коэффициентов диффузии DT зависят от температуры, концентрации, структуры, примесей, напряженного состояния и мо­гут меняться в широких пределах (КГ7—КГ16 см2-с"1 и менее). Значения коэффициентов диффузии в жидкости в основном лежат в пределах 1(Г4—1(Г6 см2-с-1. Длительность контактирования в слу­чае сварки и наплавки металлов меняется от 0,01—0,5 с (смачивание) до 0,5—10 с и более (наплавка, сварка) и зависит от погонной энер­гии и скорости сварки [120, 123].

Равновесный коэффициент распределения (k0 = ст/сж) в зависи­мости' от легирующего элемента может быть больше или меньше единицы- Если происходит снижение температуры, то k0 < 1 (1 — 0,001 для систем, относящихся к чисто эвтектическим). Если примесь повышает температуру плавления сплава, то k0 > 1 (1—3). В ред­ких случаях (для бора в германии) k0 = 15 или даже больше. При наличии интенсивного перемешивания эффективные значения коэффициента распределения k могут сильно отличаться от равно­весных и с увеличением интенсивности перемешивания стремятся к 1.

В общем случае значения эффективного коэффициента распреде­ления определяются из уравнения, полученного К. Бартоном и др.

k = kj lk0 + (1 - ko) exp (1 - /бо/D*) ], (45)

где / — скорось увеличения толщины твердой фазы; 80 — толщина ламинарного слоя; Dm = 10_5-~1(Г4 см2*с-1.

Для большинства практических случаев неизвестны точные зна­чения эффективного коэффициента распределения k, коэффициентов диффузии DT и Ож и длительности контактирования. Точное опре­деление этихГ величин в реальных металлических системах связано с большими трудностями, так как их значения в значительной сте­пени зависят от многочисленных побочных процессов.

Для большинства случаев диффузии элементов замещения эффек­тивный коэффициент распределения k можно не учитывать при решении гетерогенных задач с точностью ~0,1—0,01 %, т. е. в пре­делах точности локального рентгеноспектрального микроанализа. В этих случаях для расчета можно использовать приближенные уравнения

Crj, = ctq A. CqBIi/~D^/Dyx - j— 1, (^6)

cm = сж0 + A c0B/j/" D mDT, (47)

ГДЄ ACq = Ctq ^жО*

Уравнения (37), (38) и (46), (47) для гетерогенной диффузии при­меси неприменимы в случае контакта двух чистых разнородных металлов. В связи с этим рассмотрена задача развития химической неоднородности в зоне контактирования твердой и жидкой фаз разнородных металлов [123]. Решение имеет вид

ст = - Г-У°ж [l - f - ф(при х<0; (^8)

Vdt + Tdx L V2J/OV/J v сж= [l-<e/-JL=Y| при x>0. (49)

Уравнения гетерогенной диффузии примеси (37) и (38) и уравне­ния (48) и (49) не учитывают наличия двухфазной области, изменения коэффициентов диффузии от концентрации. Уравнения (48) и (49) могут быть использованы и при взаимодействии двух металлов в твердом состоянии. В этом случае

С - VD‘

Vda + Vdb

V-Da _ Vda + Vdb

1+фЫЬ)]при *<0; (50>

‘-ф(-іИЬ)] nP“*>0’ <51)

где сА и св —соответственно концентрации элемента А в В и В в A; Da и Db —соответственно коэффициенты диффузии А в В и В в Л.

В тех случаях, когда при соединении металлов требуется свести к минимуму ширину зоны химической неоднородности, необходимые температуру и время процесса можно определить из (37), (38) или (50), (51), задавая значения ст, ст или сАу св равными нулю, а х — равным ширине допустимой зоны гетерогенной диффузии. При определении времени контактирования для соединения металлов в твердом состоянии необходимо учитывать дополнительное время, требуемое для достижения физического контакта на всем протяже­нии контактирующих поверхностей.

Разработана методика расчета [42, 154] толщины интерметалли­ческой прослойки в зависимости от температуры процесса и времени контакта твердой и жидкой фаз. Для простоты расчета приняли диаграмму состояния взаимодействующих металлов А и В, приве­денную на рис. 4. Как правило, опасные толщины интерметалличе­
ских прослоек весьма малы в сравнении с толщинами самих взаимо­действующих тел, поэтому при расчетах эти тела в ряде случаев можно считать полубесконечными. Тогда распределение концентра­ции по толщине жидкости при растворении в ней твердого тела с уче­том нестационарности процесса можно найти по формулам, приве­денным в работе [131]. Так как выпадение интерметаллида может происходить только в том случае, если концентрация А в некоторой части жидкости больше концентрации с19 то, зная закон насыщения жидкости атомами твердой фазы и используя диаграмму состояния, можно определить толщину интерметаллической прослойки, которая выпадет при кристаллизации, в зависимости от длительности кон­такта жидкой и твердой фаз.

Суммируя толщину прослойки при t± от каждого элементарного слоя, найдем полную толщину прослойки [154]

й. = 2>=2£Е£ Д.. (52)

i=l 1=1

или, выбирая толщину Дг бесконечно малой, придем к интегралу

<53>

О

где а — то значение я, при котором с{а) = сг.

Определяя у для разных значений времени при Т = const, полу­чим зависимость толщины прослойки от времени контакта жидкой и твердой фаз.