СВАРКА И СВАРИВАЕМЫЕ МАТЕРИАЛЫ

Определение сварочных деформаций, напряжений и перемещений

4.3.1. Расчетные методы

4.3.1.1. Основне этапы расчета. Расчет сварочных деформаций и напряжений состоит из определения:

1) температурных полей при сварке;

2) свободных температурных деформаций и деформаций от структурных превращений, механических свойств материала, зависящих от температуры;

3) собственных деформаций, напряжений и перемещений.

Для проведения расчета необходимы следующие исходные

данные:

1. Характеристики сварочного источника нагрева, условия теплоотвода и теплофизические свойства материалов (коэффи­циенты теплоемкости ср, теплопроводности К, теплоотдачи с поверхности ат). Справочные данные и методы расчета тем­пературных полей приведены в главе 2.

2. Дилатометрические характеристики материалов, обра­зующих сварное соединение. В случае сварки разнородных ма­териалов или применения присадочного материала, отличаю­
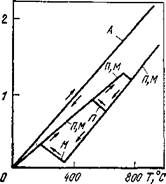
щегося от основного, эти характеристики для разных зон со­единения могут не совпадать. Примеры дилатограмм показаны на рис. 4.9.

Для приближенных расчетов может быть использована усредненная дилатограмма, соответствующая уравнению пря­мой Деа —аАТ.

Значения коэффициентов линейного расширения а для раз­личных материалов приведены в табл. 4.1. В таблице указаны также интервалы изменения температуры Т, для которых опре­делены средние значения а. Более точное определение дилатограммы требует проведения испытаний в условиях, близких к реальному сварочному циклу.

3. Для расчета деформаций и напряжений в низкотемпературной зоне, где не возникают пластиче­ская деформация, механические свойства материала могут быть представлены друмя модулями уп­ругости — при всестороннем нагру­жении К и при сдвиге G. Как вид­но из рис. 4.10, модуль G суще­ственно снижается с ростом тем­пературы. Значения G и К при комнатной температуре для ряда металлов приведены в табл. 4.1. Для учета пластических деформа­ций необходимы также данные о пределе текучести материала от. Как показано на рис. 4.11, от еще существеннее убывает с ро­стом температуры, чем G (рис. 4.11). В упрощенных методах

расчета диаграммы часто схематизируют прямой или ломаной линией. В частности, схематизированная диаграмма от для низкоуглеродистой стали показана на рис. 4.11. При Т> 870 К принимают 0Т = О.

Как правило, при расчете сварочных деформаций и напря­жений диаграмму материала а,(е,-) принимают идеализирован­ной, без упрочнения. Как пока­зывает практика расчетов, такой подход приводит к существен­ным погрешностям при опреде­лении временных деформаций и напряжений.

Более точные методы, учиты­вающие упрочнение и ползучесть, требуют для каждого материала проведения испытаний при раз-

щ,% 100

Рис. 4Л0. Зависимость модуля упру - Рис. 4.П. Зависимость предела текучести 0Т

(2]СТ№- значение0 G ^рГІ^МЗКН °Т темпеРатУРы Т И < °Т0 - значение О, при

Н —■ иизко - и средиелегированные ста - Г—293 К):

ли; А — аустенитные стали Н — низкоуглеродистые стали; JI — низколе­

гированные стали; А — аустенитные стали; А1 ~ алюминиевые сплавы; Нс—і схематизи­рованная зависимость для иизкоуглеродистых сталей

личных напряжениях, температурах и скоростях дефор­мации. Наиболее типичными являются испытания при задан­ных температуре и напряжении (на ползучесть) или при за­данных температуре и деформации (на релаксацию). Получае­мые из серии таких испытаний кривые a(t) и e(t) могут быть использованы при расчете сварочных деформаций и напряже­ний [2]. В работе [1] предложен метод пластических приближе­ний. После приближенного расчета сварочных деформаций по упрощенной модели поведения материала проводятся испыта­
ния, имитирующие условия в различных точках свариваемой детали по температуре и деформации (термодеформационный цикл). Полученные из эксперимента напряжения используются в расчете в качестве характеристики материала, отражающей его реальное поведение с учетом релаксации и упрочнения.

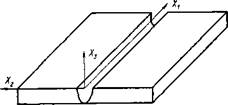
4.3.1.2. Уравнения упругопластического деформирования. При сварке в каждой точке детали возникают в общем случае 6 компонент напряжения, 6 компонент деформации и 3 компо­ненты перемещения. На рис. 4.12 показано расположение ко­ординатных осей: Х[ — вдоль шва, х2— поперек шва в плоско­сти свариваемых пластин и х3 — в направлении толщины пла­стины. Соответствующие компоненты деформации и напряже­ний обозначим tij, о,/, а перемещений —щ. Индексы i, j могут принимать значения от 1 до 3. Нормальные компоненты де-

формации и напряжений имеют оба индекса оди­наковые: Єн, Є22, Єзз

нормальные деформации ВДОЛЬ осей Хи х2, Х3, Оц, (Т22, (Тзз — нормальные на­пряжения вдоль тех же осей координат. Дефор­мации сдвига и касатель­ные напряжения имеют разные индексы: єі2, є2з,

езь 012, <Т2з, 03Ь ДЛЯ каЖД°Й компоненты деформации можно выделить наблюдаемые, собственные и свободные температур­ные деформации согласно формуле (4.1). При этом для изо­тропного материала, имеющего одинаковые свойства по всем направлениям:

баи = ett22 := еазз = еа> (4-4)

еаі2 ~ еагз == еазі = б-

Наблюдаемые деформации связаны с перемещениями то­чек тела

(4.5)

Собственные деформации связаны с напряжениями. Упру­гие деформации связаны с напряжениями законом Гука. Закон Гука записывается отдельно для деформаций изменения объ­ема и деформаций изменения формы, так как модули упруго­сти при изменении объема и формы тела различны. Изменение объема выражается через средние нормальные деформации во.

Средние деформации связаны со средними напряжениями Оо через объемный модуль упругости К:

&о = oJK, (4.6)

где

Єо = (бупри + Єупр22 4~ єупрЗз)/3) °0 = (°11 + °22 + °8з)/3- (4.7)

Часть деформации, не вызывающая изменения объема, на­зывается деформацией изменения формы, или девиатором де­формации. Компоненты девиатора деформации ец и девиатора напряжения Sn определяются по формулам:

еупр ij — Єупр ij — Ь{)Ъо,

с я I (4'8)

о// — оі/ — О{/о0, )

где 6ij — коэффициент, равный 1 для нормальных компонент (при i = j) и равный 0 для компонент сдвига (при іф]). Ком­поненты девиатора упругой деформации еущ>ц связаны с соот­ветствующими компонентами девиатора напряжения через модуль сдвига G:

еупр ij — Si/I(2G). (4.9)

Пластические деформации происходят без изменения объ­ема, только за счет изменения формы:

епл ij = епл ij - (4-10)

Уравнение связи компонент пластической деформации с компонентами девиатора напряжений

депп ij/dt = SijX. (4.11)

Способ определения коэффициента X в формуле (4.11) за­висит от принятой модели пластической деформации. Чаще всего принимается модель идеального упругопластического ма­териала без упрочнения.

В этом случае

% = (3/2ог) (дєпл ildl), (4.12)

где__________________________________

11 "Т “^22 - Ь *^33 2^12 Т" 2^23 2S|i^ , (4.13)

епл 11 + гпл 22 + епл 33 4" ^епл 12 + ^епл 23 + ^епл Зі) • (4-14)

Так как у идеального упругопластического материала в пла­стической области о; не зависит от еПл ь то пластические де­формации целиком определяются деформациями окружающей упругой зоны и условиями закрепления детали. По известным компонентам деформации можно определить компоненты на­пряжений. Процесс образования напряжений при сварке, как правило, нельзя считать простым нагружением, так как соот­ношения компонент деформации и напряжения в ходе нагру­жения существенно изменяются. Поэтому для расчета напря­

жений в упругопластическом теле необходимо весь процесс де­формирования разбить на отдельные шаги по времени. Напря­жения в конце каждого шага а,, зависят от напряжений в на­чале шага Оц' и приращений деформаций за шаг Ае,3 = е,}—Єї/. При этом изменение объема происходит по закону Гука-

°0 =■ °0 + (Ле0 — Аеа)К (4-15>

Девиатор напряжения в конце шага определяется по фор­муле (4.9) в случае упругого состояния материала, то есть при интенсивности напряжения, меньшей предела текучести. В случае пластического состояния материала:

5 g $;,/»; + «,, {sh(Ap)+m[ch (Ар)-1]} . (416)

4 ‘ ch (Ду) + ш sh (Ду)

ич = A«l;/V3/2 (Деп + Л4г + Лезз + 2Л4 + 2Дй2з + 2Де|і) ; (4.17)

ш = (3/2о() (5,^,, + S22«22 + 533«33 + 2S12«12 - f 2523«23 + 2S31«31);

(4.18)

Ду = (G*/a*) V6 (Де^, + Де|2 + Де33 - f 2Дй|2 4- 2Де23 4- 2Де31) , (4.19)

где а/ и о, — интенсивность напряжения в начале и конце шага (для упругопластического материала без упрочнения она равна пределу текучести); G* и о,* — средние значения модуля упругости и интенсивности напряжения за шаг.

4 313 Расчет деформаций и напряжений Все известные методы расчета являются приближенными, т. е. опираются на ту или иную модель процесса. Упрощения могут касаться как схемы напряженно-деформированного состояния, так и модели поведения материала.

Наиболее простыми являются методы расчета по одноосной схеме [1]. Для упрощения расчета предполагают, что все точки шва одновременно нагреваются, затем одновременно остывают. При этом в незакрепленной пластине перемещения поперек шва происходят свободно, а напряжения возникают только вдоль шва (Оц) из-за неравномерного по ширине нагрева пластины. В действительности нагрев различных поперечных сечений пла­стины происходит неодновременно, поэтому образуются также компоненты напряжения а22 и сг12. Точность расчетов по одно­осной схеме невысока, однако она обладает простотой и дает на­глядную и качественно верную картину образования напряже­ний в пластине во время и после сварки.

При сварке пластин небольшой толщины компонентами на­пряжения в направлении толщины пластины можно пренебречь и проводить расчеты по двухосной схеме (плоского напряжен­ного СОСТОЯНИЯ), учитывая ТОЛЬКО компоненты ВДОЛЬ осей Х и х2 (см. рис. 4.12). Толщину пластины следует оценивать по отношению к ширине зоны термического влияния шва. Для ду­говой сварки небольшой следует считать толщину до 20 мм, для ЭШС — до 100 мм. В случае сварки больших толщин необхо­димо проводить расчет по трехосной (объемной) схеме, при этом процедура расчета существенно усложняется. Существует ряд аналитических решений по теории упругости и теории пластич­ности [1]. Однако наиболее универсальными являются методы расчета на ЭВМ, например метод конечных элементов [4], ко­торый не требует упрощения формы детали и используемых в расчете диаграмм свойств материала.

При выборе метода расчета следует исходить из требуе­мой точности, а также из того, какие напряжения и деформа­ции необходимо определить. Более грубые методы, основанные на упрощении схемы напряженно-деформированного состояния и свойств материала, дают существенную погрешность при оп­ределении временных напряжений и приемлемую точность при оценке остаточных напряжений. В наиболее ответственных слу­чаях результаты расчета следует сопоставить с данными экспе­риментального измерения деформаций напряжений и переме­щений. Методики таких измерений описаны в 4.3.2

4 3.1.4 Расчет перемещений Для точного расчета перемеще­ний в свариваемых деталях вблизи шва необходимо применять методы теории пластичности и ползучести, учитывать зависи­мость свойств материала от температуры. Целесообразно ис­пользовать численные методы, рассмотренные в 4.3.1.1.

Для оценки перемещений вне зоны шва можно использовать более простые методы. Продольные остаточные перемещения в сваренной детали могут быть рассчитаны методами сопротив­ления материалов, если приложить к детали усадочную силу, действующую вдоль оси шва (см. рис. 4.1). Усадочная сила Рус пропорциональна величине остаточных пластических деформа­ций в зоне шва:

РуС= § е. цЕЫхг, (4.20)

~~ЬП

где еи — остаточная пластическая деформация; 2Ьи — ширина

3 Gk

зоны пластических деформаций; Е= —модуль упругости

при одноосном растяжении; 6 — толщина пластины.

Для весьма жесткого тела

Рус ш = ~ 230000 + 3,58] qlve, (4 21)

L Я (^с^расч) “Г 12600 J

где q/vc — погонная энергия сварки (q — эффективная мощ­ность, Вт; ис — скорость сварки, см/с); брасч — расчетная тол­щина сварного соединения, см.

При сварке двух пластин толщиной 61 и 62 встык или в угол врасч — - 1 _■ 2 ; при приварке пластины толщиной 61 втавр или внахлестку к пластине толщиной й2> <5расч =—^ . Фор­

мула (4.21) справедлива для ql(vc, 6расч) в диапазоне от 4000 до 38 000 Дж/см2 при естественной теплоотдаче и толщинах металла до 20—25 мм. Погонная энергия может быть опреде­лена по площади поперечного сечения наплавленного ме­талла FH.

q/v с = QvF„, (4.22)

где Qv — коэффициент, зависящий от способа сварки. Значения для Fн в см2 приведены в табл. 4.2.

Для тела ограниченной жесткости и при эксцентричном дей­ствии усадочной силы:

Рус *------------------------------------------------------------------------------- (4.23)

Рус --

{е1 i - j - Є2/І2 1 /F)/or

где /1, h — моменты инерции сечения относительно главных осей; еи е2 — эксцентриситеты приложения усадочной силы от­носительно тех же осей; F—площадь сечения; <гт — предел те­кучести материала. Знаменатель дроби в (4.22) не может быть менее 0,5.

Формула (4.21) справедлива, когда площадь зоны пластиче­ских деформаций, равная примерно Рус ж/ат, не превышает 25—30 % от всей площади поперечного сечения F.

Для случаев. многопроходной дуговой сварки и точечной сварки также может быть определена усадочная сила по фор­мулам, приведенным в [1].

При сварке с зазором поперечные перемещения кромок до­стигают максимума итах в момент прохождения источника:

V = a ql(cpvc6), (4.24)

где а — коэффициент линейного расширения материала; ср — удельная объемная теплоемкость; q/vc— погонная энергия сварки; 8 — толщина пластины.

Поперечная усадка при сварке

Дпоп = ^утах> (4-25)

где А — коэффициент, зависящий от способа и условий сварки.

Усадка увеличивается, если на стадии нагрева полностью ис­ключить раздвигание от оси шва свариваемых пластин при рас­ширении металла, а на стадии остывания устранить все препят­ствия для сближения пластин в направлении к оси шва. При этом А приближается к максимальному значению, равному 2. В реальных случаях А<2. Например, при электрошлаковой сварке А «1,6. При дуговой сварке встык с полным прсщлавле - нием, как правило, А = 1—1,2. Формула (4.24) справедлива также для алюминиевых, магниевых и титановых сплавов.

В случае неполного проплавления (например, при приварке к пластине других элементов угловыми швами) поперечная усадка уменьшается (табл. 4.3).