СТРУКТУРА И СВОЙСТВА ГАЗОНАПОЛНЕННЫХ ПОЛИМЕРОВ
РАЗРУШЕНИЕ ПЕНОПЛАСТОВ С ВЗШЮПРОНИКАЮЩИШ ЯЧЕИСТЫМИ СТРУКТУРАМИ ПРИ ОДНООСНОМ СЖАТИИ
Задачей настоящего раздела работы является рассмотрение в статистическом аспекте кратковременной прочности лёгких жестких пенопластов ( ^"^100 кг/м3) при одноосном сжатии.
Остановимся прежде всего на использованнной оценке ячеистой структуры лёгких пенопластов. В качестве важнейших параметров ячеистой структуры можно назвать линейные размеры макроячейки/^ и коэффициент формы ячейки К, равный отношению линейных размеров ячейки в направлении вспенивания к размерам ячейки в направлении перпендикулярно вспениванию; длину тяжа / , толщину тяжа в средней части его с/т> толщину тяжа вблизи узла d^ , коэффициент формы тяжа К , равный отношению с/^,/с/т> и коэффициент разнотолщинности тяжа К, равный отношению 2( G^ - с/т) / L^t коэффициент искривления тяжа Ки, равный отношению 2( k^ - гДе h^vi h^ - стрела про
Гиба тяжа, измеренная у одного и того же тяжа с противоположных сторон, толщину узла d и коэффициент формы узла К, равный от-
</ «У
Ношению d / dT* Предложенная нами методика измерения указанных параметров /158/ заключается в непосредственном измерении линейных размеров фрагментов газоструктурных элементов с изовражения на экране, получаемого с помощью диапроектора. При этом образец для испытаний» помещаемый в диапроектор, имеет переменное сечение по толщине, а в периферийной зоне толщина образца существенно меньше линейных размеров ячеек. Линейные размеры ячеек овального типа ZQ определяли с помощью диапроектора.
Результаты оценки параметров элементов макроструктуры для ППУ-3 и ППУ-75, а также для пенофенопласта ФРП-I представлены в табл.^ьЗ» На экспериментальную точку брали от 15 до 50 элементов макроструктуры, что обеспечивало точность в пределах 20% при доверительной вероятности 0,95. При этом коэффициент вариации в случае контроля
|
Таблица 4.3* Параметры элементов ячеиотой структуры лёгких пенопластов.
|
Кт, К, Кр» Ки составил 12, 17, 32, 7Q$ соответственно. Учитывая столь существенное значение коэффициента вариации при определении параметров макроструктуры, можно ожидать проявление по этой причине неоднородности пенопласта в случае определения прочности.
Из таблицы 4.3 видно, что К и К, характеризующие различие толщины тяжей в периферийной и средней зонах, близки к единице. Следовательно, сечение тяжей хотя и увеличивается вблизи узлов, однако его изменение мало. Коэффициент искривления тяжей Ки существенно меньше коэффициента разнотолщинности К, то-есть тяжи пра&-
Г
Тически не искривлены. Довольно большая величина параметра К у
У
Различных пенопластов указывает на значительное содержание полимера-основы в узлах ячеек.
У лёгких пенопластов могут быть получены взаимопроникающие
- 207 -
Ячеистые структуры, когда наряду с ячейками полиэдрической формы в пенопласте одновременно присутствуют ячейки овальной формы. При этом структуры различаются существенно линейными размерами ячеек. В качестве такого примера в таблице 4.3 представлены данные по ППУ-3 кажущейся плотности 25,9 кг/м3.
В настоящем разделе рассмотрены пенопласты, которые имеют взаимопроникающие ячеистые структуры нескольких уровней /143-144, 158, 196/. В предельном случае они сводятся к обычным пенопластам с мономодальной структурой. Впервые А. Шутовым были обнаружены у пенопластов микроячейки в элементах макроструктуры фенольных и полиуре- тановых пенопластов, что приводит к образованию бимодальных структур /36, 41-42/. Механизм образования бимодальных структур, связанный с наступлением вторичной волны вспенивания из-за вторичного пересыщения газа в матрице, описан в /36, 41-42, 231/ с указание* возможности управления: получением микроячеистой структуры как путём изменения температурно-временных интервалов внешней тепловой нагрузки, так и за счёт изменения вида вспенивающего агента. Позднее на примере карбамидоформальдегидных пенопластов нами показана возможность образования взаимопроникающих ячеистых структур нескольких (более двух) уровней /143-144, 158, 196/,
Так как прочность является одним из основных эксплуатационных показателей пенопластов, представляется важным определить уровень изменения прочностных свойств пеноматериалов с взаимопроникающими ячеистыми структурами при учёте влияния различных параметров макроструктуры.
Расчёт прочности пеноматериала выполнен исходя из использовавшихся ранее моделей в виде 14-гранной ячейки для лёгких пенополимеров и в виде кубической решетки для ячеек овальной формы /135, 196^ При этом полагаем, что тяжи толщиной^ и узлы лёгкого пенопласта' с 14-гранной формой ячеек состоят из пеноматериала с ячейками овального типа диаметром ф, При дополнительном наличии микропо
ристой структуры элементы вторичной ячеистой структуры овального типа можно представить состоящими из микропористого материала с микроячейками овального типа диаметром ф. Тогда по аналогии с /135/ из геометрических рассмотрений модели легко выразить кажущуюся плотность пенопласта с взаимопроникающими ячеистыми структурами:
T _ 3 т ( 2 + ji)2
С i + /т)3
X 3 к * к3
(I +"л')3
|
(4.28) (4.29) (4.30) |
2 2 ~3
J, IbLLh - . . (4.31)
<2< i + jy3 а-уО3
Где: р - отношение толщины тяжа к его длине у 14-гранной модели ячейки;J2 и J3 - отношение толщины тяжа к его длине у модели
И
Макро и микроячейки типа кубической решетки; и - кажущаяся плотность пеноматериала в тяже модели 14-гранной и кубической решетки макроячейки; р - плотность полимера-основы.
Таким образом, выражения (4.28) - (4.31) позволяют легко определить кажущуюся плотность У*4 пенопласта для различных вариантов взаимопроникающих структур, регламентируемых параметрами уЗ, ' • Б частности, из (4.28) -(4.31) видно, что изменение параметров ft и Д за счёт увеличения или уменьшения объёмного содержания ячеек овального типа приводит к определённому изменению параметра ft в 14-гранной модели ячейки при неизменной кажущейся плотности пенопласта.
- 209 -
Определим влияние указанных параметров моделей на прочность пенопластов. Аналогично /135, 196/, прочность при сжатии G* пенопласта с взаимопроникающими ячеистыми структурами рассматриваемого типа можно выразить в виде:
|
(4.32) |
|
,_т__ Юг{г |
А4 ^2Еф-(2+уЗ)2
Or = ( .л - )
|
„. а/. |
|
(4.33) |
2 2 2 2 Е/т (2 )
4dZ{r
Причём модуль упругости определяется в виде:
'/(г
-- при
|
Е Л = I» |
|
Т? |
2 J* т
/V
/Гё7
|
2 Л |
|
' 2 j т |
При ------
|
2 + |
|
J5 |
|
I + А> |
<■ 1 +JV
У/г /V ^
2+/' 2 + уЗ"
|
С г ♦ /:) |
|
Е -1- -< Е |
|
^ <р <1 - > |
И
Где: Е - модуль Юнга полимера-основы; Ет и Ет - модуль Юнга пеноматериала в тяжах 14-гранной и кубической решетки макроячейки; у? - отношение толщины тяжа к его длине у 14-гранной модели микроячейки.
Таким образом, формулы (4.31), (4.33) определяют в параметрическом виде расчётное семейство кривых (j Q = (Э прочности пенопластов с взаимопроникающими ячеистыми структурами.
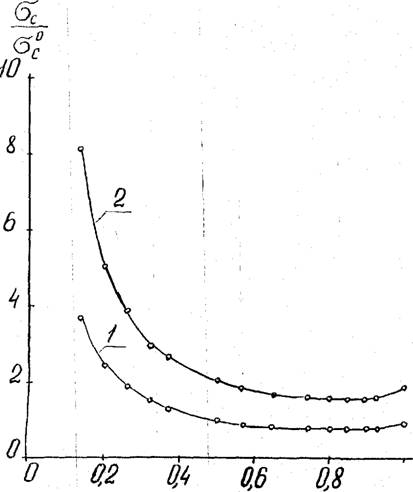
Для оценки влияния параметров макро - и микроструктуры исследуемых пенополимеров на их прочность в качестве примера были расчитаны две кривые из этого семейства. У полимера-основы жесткого пенополиуретана исходные характеристики были приняты следующие: Е = 3 ООО Ша;j0=I200 кг/м3. Тогда, например, для ^ = 22 кг/м3 с двумя типами взаимопрони-». кающих ячеистых структур ( /р = I ) получаем расчётную кривую прочности при сжатии пенопласта, представленную в приведенных координатах на рис. 4.19 (кривая I). Для исходного ППУ без взаимопроникающих ячеистых структур расчётная прочность составила <о q = 0,075 Ша. Из (4.28) - (4.33) легко показать, что для других пенопластов с различными полимерами, различающихся значениями Ей р, но с одинаковой приведенной кажущейся плотностью £/р и /р, приведенная прочность^. /<5 « Б зависимости от параметра структуры овального типа
О j
)fT /р выражается одинаковым образом.
Из рис. 4.19 ( кривая I ) видно, что при снижении параметра /р. с I до 0,8 прочность пенопластов с взаимопроникающими ячеистыми структурами снижается, хотя и незначительно, а затем сохраняется неизменной. Это можно объяснить резким снижением модуля упругости пенопласта с овальной формой ячеек Ет в рассматриваемом интервале изменения параметров за счёт значительного перераспределения полимера-основы в тяжах и узлах модели кубической решетки. На втором
Участке кривой при 0,14 ^ /р ^ 0,6 влияние изменения параметра. и *
/р на оказывается более сильным. Это обусловлено более медленным снижением параметра Ет структуры овального типа при дальнейшем снижении отношения t^ /р и одновременным более резким возрастанием жесткости тяжей в 14-гранной модели при их продольно-попдеч - ном изгибе.
На рис. 4.19 (кривая 2) в качестве второго примера представлены результаты расчёта приведённой прочности карбамидоформальдегидного пенопласта МФП с макроструктурой полиэдрического типа в зависимости от параметра структуры / ^ Кажущаяся ПЛОТНость пенопласта
|
|
|
To Kr. tv |
IviCo 4.19. Зависимости приведенной прочности от приведенного параметра ячейкой структуры пенопластов с взаимопроникающими ячеистыми структурами при постоянной кажущейся плотности пеноматериала. Для пенополиуретана (I) 22 кг/м3;
И, 14 * О"1' для 1#П (2) ^ 10 кг/м3; = °'25;
О
Составила 10 кг/м при величине параметра микропористой структуры
/р - 0,25, плотности полимера-основы р - 1500 кг/м3 и изменении параметра ячеистой структуры овального типа в пределах 0,14<^ f /^ Из рис. 4.19 (кривая 2) видно, что у взятого пенопласта с тремя уровнями взаимопроникающих ячеистых структур прочность при сжатии может измениться ещё более резко в зависимости от изменения параметров Ет, Е^ при неизменной кажущейся плот
Ности пенопласта. Таким образом, представленные данные показывают, что меняя параметры макроструктуры на различных уровнях за счёт изменения технологии получения пенопласта, можно добиться увеличения прочности пенопласта с взаимопроникающими ячеистыми структурами в несколько раз при неизменной его кажущейся плотности.
Сопоставление результатов расчёта с прямым опытом целесообразно провести, используя статистическое исследование разрушения такого пенопласта, поскольку известно /153/, что масштабный фактор образца, разрушение ячеек с поверхности образца при его вырезке, неоднородность пеноматериала могут существенно повысить или понизить искомый показатель.
Выполненные нами расчёты статистических моделей таких пенополимеров показали /158/, что и в случае сжатия сохраняются зависимости влияния структуры пеноматериала и геометрических факторов образца на показатели свойств аналогично (4.26-4.27);
Г,/разр Г 7
Бс = кв а V™-- >а(1 ) + §COJ ; (4.34)
Где:С1- среднее значение прочности ячеек; коэффициент вариации;/"7- общая площадь поперечного сечения образца;/7. - пло-
UcLо kJ
Щадь поперечного сечения поверхностного слоя образца; $(2), )- - функции Лапласа; Кв - поправочный коэффициент для базового образца пенопласта; J^ - доля разрушенных тяжей в поверхностном слое пенопласта.
- 213 -
Проведем сопоставление результатов определения прочности пенопластов, полученных расчётным и опытным путями. Для испытаний были взяты жесткие ППУ марок ППУ-3 и ППУ-307, получаемые методом заливки в форму. Механические испытания ППУ проводили при температуре 293 +2К. Образцы для испытаний имели форму параллелепипеда с размерами 30 хЗО х45 мм. Прочность пенопластов определяли на испытательной разрывной машине типа БРП-5-3 при скорости деформации 0,0056 сЛ, Для оценки влияния масштабного фактора на прочность пенопласта вырезали также образцы в форме параллелепипеда с отношением высоты к ширине 1,5 :1 и поперечными размерами 10 х!0, 15 х 15, 50 х50 мм. На одну экспериментальную точку при испытании на сжатие брали от 50 до 100 образцов. Коэффициент вариации составил 7,8| у ППУ-3 и 12,7$ у ППУ-307.
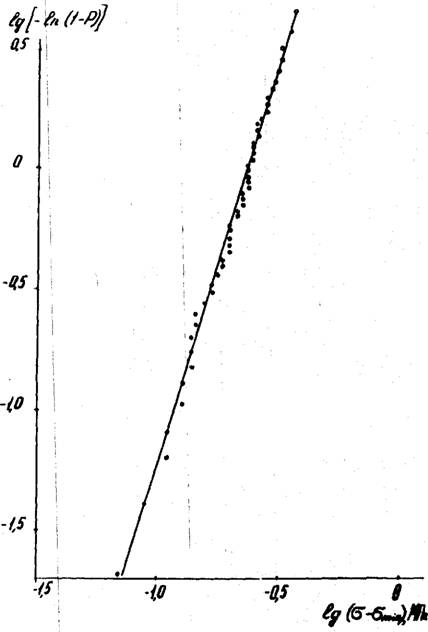
Оказалось, что распределение прочности при сжатии ППУ хорошо описывается уравнениями (4.27), (4.34). В качестве примера на рис. 4.20 представлена зависимость вероятности разрушения образцов ППУ-3 с взаимопроникающими ячеистыми структурами от разрушающего напряжения при сжатии. По измеренному углу наклона полученной прямой был расчитан параметр однородности 8 , представленный в таблице 4.4. Из таблицы 4.4 видно, что значения эффективного коэффициента использования площади (I - z^-г) х Ф(г) + Ф ( и разрушенной площади образца I - Ф( 2 .) + Ф( ^ ) J при достижении критической нагрузки близки к величинам, полученным у пенопластов в работе /153/ при испытании на растяжение.
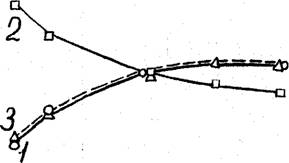
При оценке влияния масштабного фактора на прочность пенопластов значение параметра X в формуле (4.34) для ППУ с взаимопроникающими ячеистыми структурами было найдено равным 0,24 /158/. Результаты определения (о различными методами представлены на рис. 4.21. Из рис.4.21 видно, чаю с уменьшением толщины образца до 10 мм значение прочности не только не увеличивается, как следовало ожидать из формулы Вейбулла (4.19), но, наоборот, резко уменьшает-
|
|
Рис, 4.20. Зависимость вероятности разрушения ППУ-3 от разрушающего напряжения при сжатии в координатах Вейбулла.
Q
|
|
M-
|
40 L 60 Fl. MM |
|
20 |
0
Рис. HcL-
Сквисимость разрушающего напряжения 1ШУ-3 с взаимопроникающими структурам^ при сжатии от толщины образца: i - прямой эксперимент; 2>;3 - расчёт по формулам Вейбулла и
|
Oc |
I I
1 Лос'6) соответственно.
[
|
Таблица 4.4, Результаты статистических испытаний базовых образцов жестких ППУ в условиях одноосного сжатия.
|
Ся. В то же время сопоставление кривых I и 3 на рис. 4.21 показывает, что выведенный обратный в сравнении с монолитными материалами эффект (формула 4.34) влияния масштабного фактора на прочность пенопластов хорошо согласуется с экспериментом.
Сопоставление также показало удовлетворительное соответствие расчётных и опытных данных при определении прочности образцов с взаимопроникающими ячеистыми структурами. Так, прочность ППУ-3 с взаимопроникающими ячеистыми структурами при сжатии для образца сечением 40 х40 мм в прямом опыте составила 0,090 Ша, в то время как у аналогичных образцов с полиэдрической формой ячеек она была 0,074 Ша, то-есть на 22$ ниже /158/.
Таким образом, при исследовании макроструктуры лёгких пеноплае-
Тов, имеющих одновременно полиэдрическую и овальную форму ячеек установлено, что у пенопластов с взаимопроникающими ячеистыми структурами овального и полиэдрического типов могут быть достигнуты различные уровни прочностных свойств пеноматериала при неизменной кажущейся плотности. Установлен закон распределения прочности при одноосном сжатии жестких пенопластов и обратный эффект влияния масштабного фактора на прочность пенополимеров по сравнению с монолитными материалами. Определена степень повреждённости образцов перед их разрушением.
Научные результаты исследований, изложенные в данной главе» заключаются в том, что впервые выполнены теоретические расчёты диаграмм сжатия эластичных пенопластов при больших деформациях с учётом влияния геометрических параметров газоструктурных элементов, спектра распределения жесткости газоструктурных элементов, релаксационных свойств полимера-основы. Объяснён механизм деформ*» рования пенополимеров на различных стадиях их сжатия и выведены уравнения всех основных типов диаграмм сжатия эластичных пенопластов. Установлено, что на диаграммах сжатия эластичных пенопластов наблюдается крутой начальный участок, плато либо медленный рост нагрузки на втором участке и быстрый рост нагрузки на третьем участке и объяснён механизм возникновения отмеченных особенностей. Расчётным путём показано, что в зависимости от однородности пенопласта и релаксационных свойств полимера - основы, на 2-м участке диаграммы может появиться максимум, либо наблюдается рост нагрузки с различной скоростью.
Результаты были использованы при выборе и разработке технологии производства эластичных ППУ для сидений, отличающихся повышенной комфортностью.
Б то же время показана некорректность интерпретации функции деформации в уравнении Раша, широко распространённом на практике, как характеристики макроструктуры, поскольку эта функция связана
Также с одновременным наложением других факторов - спектра распределения жесткости газоструктурных элементов и релаксационных свойств полимера-основы.
Впервые выполнены теоретические расчёты диаграмм сжатия эластичных пенополимеров с искривлёнными тяжами. Оценено влияние кривизны тяжей при возникновении остаточной деформации пенополимера на снижение жесткости пеноматериала, увеличение деформации при критической нагрузке сжатия, характер изменения деформации сжатия вплоть до вырождения 2-го участка на диаграмме сжатия. Результаты были использованы при выборе условий по длительному использованию эластичных ППУ в деформированном состоянии, а также для определения возможности упаковки, транспортировки и хранения этих материалов в сжатом состоянии.
Выполнены теоретические расчёты диаграмм растяжения пенопластов низкой кажущейся плотности. Впервые обнаружен 5- образный начальный участок на диаграмме растяжения и объяснено увеличение модуля упругости на 2-м начальном участке в сравнении с модулем упругости на 1-м начальном участке за счёт ориентации тяжей при их продольно-поперечном изгибе. Позднее этот эффект был экспериментально подтверждён различными авторами.
Выполнены теоретические исследования разрушения эластичных и жестких пенопластов при растяжении на основе рассмотрения статио - тических моделей макроструктуры пенополимеров. Определена степень повреждённости образцов перед разрушением, выявлены виды распределения прочности ППУ. Установлен закон влияния масштабного фактора образцов на прочность при растяжении пенополимеров, в общем, противоположный полученному Вейбуллом для монолитных материалов. Установлено, что размер ячеек не влияет на прочность пенопластов. Показана несостоятельность попытки рассмотрения в ряде работ разрушения пенополимеров на уровне ячеистой структуры из
- 219 -
Анализа ячейки как деффекта материала в модели Гриффитса.
Выполнены теоретические исследования разрушения жестких пенопластов в условиях сжатия на основе статистической модели макроструктуры. Установлены законы распределения прочности при одноосном сжатии жестких пенопластов и обратный эффект влияния мас - штабно1$$Й§Р$рочность пенополимеров по сравнению с монолитными материалами. Определена степень повреждённости образцов перед их разрушением.
Показано, что у пенопластов с взаимопроникающими ячеистыми структурами могут быть достигнуты значительно более высокие уровни прочностных свойств пеноматериала при неизменной кажущейся плотности в сравнении с пенопластами, имеющими мономодальную макроструктуру.