СТРУКТУРА И СВОЙСТВА ГАЗОНАПОЛНЕННЫХ ПОЛИМЕРОВ
РАЗРУШЕНИЕ ЭЛАСТИЧНЫХ ПЕНОПЛАСТОВ ПРИ ОДНООСНОМ РАСТЯЖЕНИИ
Разрушение полимерных материалов является сложным процессом, который включает разрушение структурных элементов различных масштабов /18, 227-229/. В частности, наличие во вспененном полимерном материале ячеистой структуры приводит к специфическому его разрушению, связанному с разрывом тяжей (стержней) и стенок макроячеек /197, 230/. Представленные в литературе данные по исследованию разрушения пенопластов касались в основном оценки влияния размеров ячеек, объёмного содержания полимера и степени замкнутости ячеек на прочность пенополимеров /48, 51, 27, 36, 80-81/. Поэтому на примере эластичных ППУ нами рассмотрен /155/ на уровне ячеистой структуры механизм и характер разрушения пенопластов в статистическом аспекте.
Эластичный ППУ низкой кажущейся плотности характеризуется довольно беспорядочным распределением элементов макроструктуры по различным параметрам. Основная масса полимера-основы сосредоточена
- 190 -
В тяжах и лишь небольшая часть С ~5$) - в стенках ячеек. Тяжи не ж*» кривлены и входят своими концами в узлы. У лёгкого недеформирован - ного ППУ длина тяжей существенно (в ~15 раз) превышает их толщину, а в предразрывном состоянии это соотношение может превысить 50. Б случае растяжения образца тяжи располагаются параллельно друг дру1у в направлении приложения нагрузки. Разрушение тяжей до разрыва образца происходит по объёму равномерно и это даёт возможность ограничиться рассмотрением произвольного сечения образца. Другое важное положение заключается в допущении мгновенного (в сравнении с продолжительностью разрушения образца) перераспределения нагрузки от разорванных тяжей на соседние тяжи. Поэтому модель ячеистой структуры ППУ-Э при больших деформациях, близких к предразрывным, можно представить в виде тяжей, расположенных в слое параллельно друг другу. Каждому тяж^ соответствует определённый объём порового пространства, который можно считать одинаковым для различных тяжей, а прочность элемента такой структуры (э определяется отношением разрушающей нагрузки к площади поперечного сечения соответствующего элемента структуры. Тогда начало разрушения материала будет определяться прочностью наиболее слабого элемента.
Полагаек, что в некотором сечении к тяжам приложены равные усилия, а прочность (о в сечении распределена по нормальному закону. Нормальный закон распределения прочности у исследованных ППУ-Э косвенно подтверждён нами экспериментально из диаграмм сжатия образцов /155/. Влияние давления газа в ячейках здесь исключено, а деформация образцов при сжатии в закритической области определяется распределением жесткости (и прочности) тяжей. Действительно, за - критическая область определяется резким изменением жесткости образца в месте перегиба на диаграмме сжатия вследствие достижения критической нагрузки тяжей. В качестве примера на рис.4.12 представлены плотности распределения критических нагрузок элементов
!
|
5 |
Ментов макроструктуры |при первом цикле сжатия, совмещены i графиком нормальной плотности вероятности у Ш1У-201-1 иа ППУ-Э-35-0,8 (б), 11ПУ-75 (в).
- 192 -
Макроструктуры, полученные из диаграмм сжатия графическим дифференцированием.
Из рис.4.12 видно, что спектры распределения критической нагрузки тяжей при сжатии, описываемые в данном случае в виде гистограмм, могут быть различными. Так, структура ППУ-201-I и ППУ-75 неоднородна: закон распределения критической нагрузки тяжей при степени сжатия до 60% близок к нормальному с коэффициентом вариации 29,3 и 18,5$ соответственно (рис. 4.12а, в), то-есть макроструктура ППУ-201-I значительно более неоднородна. В то же время структура ППУ-Э-35-0,8 оказалась более однородной и коэффициент вариации для этого распределения составил лишь 3,9$ (рис.4.126)*, причём в спектре ППУ-Э-35-0,8 имеются две компонеты:узкая равномерная с высокой плотностью вероятности и более широкая с нормальным законом распределения. Узкая компонента, характеризующая однородную структуру ППУ-3-35-0,8, обусловливает появление на диаграмме сжатия плато.
Предложенная методика получения спектра и оценка из него параметров распределения (среднее значение критического напряжения элементов структуры, коэффициент вариации, показатель эксцесса и асимметрии) представляется весьма удобной и информативной. Эта характеристика позволяет количественно оценить нелинейный характер диаграммы сжатия ППУ-Э.
При приложении нагрузки часть тяжей, относительная доля площади которых в сечении составляет /у * разрушается. Когда номинальное напряжение (о достигнет критического уровня, фиксируется номинальное напряжение, равное разрушающему (5"в. Ему соответствует среднее действительное напряжение в сечении СГК, а относительная неразрушенная площадь перед разрушением составляет Ф.
Тогда, учитывая сделанные допущения, нами была выражена /155/ зависимость прочности (э через площадь поперечного сечения образца F, аналогичная представленной в работах /120, 227-228/:
^в = <omin + —— ; ( 4.19)
• /ГУВ
Где: С, " параметры распределения, характеризующие
Пеноматериал,
А также аналогичную полученной ранее /120, 227-228/ для монолитных материалов:
(5Г I - Ш)./ ф(г) + 0,5 / ; (4.20 )
±i
Где: среднее значение прочности ячеек; - ъО~ - коэффициент вариации;
2 - аргумент функции Лапласа;
Ф(ЗГ )- функция Лапласа, причём максимум выражения в правой части можно найти методом проб.
|
I - |
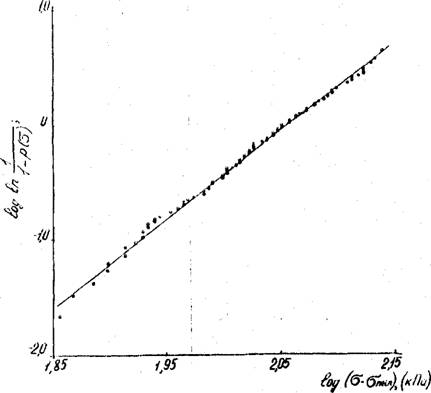
Проведём оценку результатов испытаний ППУ-3, используя получек ные расчётные зависимости. Обработка экспериментальных данных показала, что прочность ППУ-Э часто довольно точно описывается нормальным законом распределения /155/. Более точно экспериментальные данные для ППУ-Э описываются, как правило, распределением Вейбулла. В качестве примера на рис. 4.13 представлено интегральное распределение прочности ППУ-Э-35-0,8 в координатах Вейбулла. Это позволило методом последовательных приближений определить показатель однородности "в", а также параметры С и Сo'rnin в формуле (4.19). Далее найден аргумент функции Лапласа Z в формуле (4.20), соответствующий максимальному значению правой части формулы. При этом критическая разрушенная площадь образца по отношению к первоначальной составит
2) + О,5J, а эффективный коэффициент использования площади равен К ъ = (I - Тйз ) ) + 0,5 . Результаты выполненных * L J
Расчётов представлены в таблице 4.1,
Из табл. 4,1 видно, что гетерогенность ППУ-Э, оцениваемая величиной параметра & в формуле (4,19), довольно большая. Коэффициент использования площади напряженных элементов ППУ-Э при рая-
|
|
П;. ч„ i л. аилиииыисть вероятности разрушения Ш1У-У-ЗЬ-0,Ь от раз
|
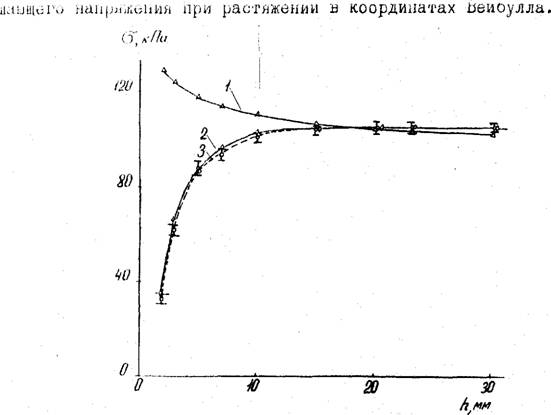
Зависимость разрушающего напряжения ППУ-3-25-3,2 при истяжении от толщины образца, расчитанная по формуле Вейбулла L), по предложенной (fcodmvjifi ( ?) „ ™ - |
Таблица Результаты статистической оценки прочности эластичных пенополиуретанов.
|
Образец |
Диаметр пор, мм |
Уравнение (4.19), где Г в см2 |
Ша |
2 |
% |
V* |
Гх% |
|
ППУ—Э— -35-0,8 |
0,8 |
1,108 <0 = 0,90+--- - Б ^1/7,8 |
0,197 |
1.7 |
8,0 |
82,7 |
4,5 |
|
ППУ-75 |
1,2 |
_ 0,181 <Эвв 0,82+ —— YI/4,2 |
0,099 |
1,9 |
5,8 |
86,1 |
2,9 |
|
ГШУ-201- - I. |
1,5 |
, 0,225 бв= 0,38+ --------------- ^1/3,8 |
0,059 |
1,5 |
11,6 |
76,5 |
6,7 |
|
ППУ-Э - -25-3,2 |
3,8 |
. 0,479 <5В= 0,72+ --------- ^1/4,4 |
0,105 |
1,6 |
10,8 |
78,0 |
5,5 |
Рыве KQ находится в пределах 78-86$, а разрушенная площадь перед разрывом Гх составляет 3...7$»
Для оценки влияния масштабного фактора на прочность ППУ-Э была расчитана по формуле Вейбулла (таблица 4.1) для ППУ-3-25-3,2 зависимость (э от толщины образца при ширине его в рабочей части 26 мм. в
Кривая I (рис.4.14) получена при обработке результатов испытаний 100 образцов с размерами лопаточек в рабочей части 26 х20 х50 мм. Из рис. 4.14 видно, что расчёты по формуле Вейбулла (кривая I) и прямой эксперимент (кривая 3) дают противоположные результаты: при уменьшении толщины образца прочность в прямом эксперименте не только не увеличивается, но, наоборот, довольно резко снижается.
Естественно предположить, что эта аномалия обусловлена разру - - 196 -
Шением тяжей с поверхности образцов при их изготовлении и это учитывается в предложенной нами /155/ модели (рис, 4.15, зоны а, в). Очевидно, что на расстоянии, превышающем длину тяжа d от поверхности среза, тяжи не могут быть разрушены при вырезке образцов. В я то же время все тяжи, прилегающие к поверхности среза, окажутся разрушенными. Тогда, как показано нами в /155/, с учётом поправки на разрушенные с поверхности образца тяжи прочность ППУ-Э можно выразить в виде:
(Э * К • б * ( I - J-Ш^ ) ; (4,21)
£1 - В
Где: (о - фактическое номинальное значение разрушающего напряжения;
(Э - значение прочности по Вейбуллу, расчитанное из резуль*
П*
Татов испытаний базовых образцов сечением > ; /"*
К0 = 1/(1 ~оС ) _ поправочный коэффициент к формуле
Вейбулла для базового образца;
И.
- доля разрушенных тяжей в поверхностном слое образца на глубине < d ; /разр~" площадь образца в сечении занимаемая тяжами, частично разрушенными при вырезке образца; F - общая площадь поперечного сечения образца.
Диаметр пор^связан с длиной тяжей пенопластов зависимостью /160/:
Из физических соображений ясно, что 0 Допуская ли
Нейную зависимость степени разрушения тяжей по толщине на глубине d, можно принять
^=0,5. (4.23)
Величина /~"^а3рможет быть выражена в виде:
/>зр (4.24)
- I97
I I
M и
1ШШ1Н
'- >- '---- V-----
A 5 5
Рис. 4Л5о Продольное "сечение образца ППУ при растяжении з случае прсдитаьи^ши'статистической моделью: а, в - краевые зоны;
{} - центра л таи зона.
|
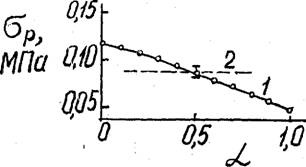
Рис. 4Л6. Зависимость прочности при растяжении ППУ-Э-25-3, от величины параметра JL для образцов толщиной 5 мм: 1 - расчёт; 2 - прямой эксперимент. |
- 198 -
Trq'.X - длина периметра образца в сечении, причём ^ ^ 2 с/.
|
) + 0,5 / ; (4.25) |
Тогда, подставляя выражения (4.22) -(4.24) в формулу (4,21), получим выражение для номинального значения прочности образцов разного сечения. В частности, для ППУ-Э-25-3,2, у которого диаметр пор оказался равным 3,8мм, формула (4.21) может быть записана в виде:
<5* ----- ( I -0,5-^р уа<1
0,873 F L
Как видно из рис, 4.14, результаты расчёта по формуле (4.25) и полученные опытным путём имеют хорошее совпадение: расхождение не превышает 6%, Следовательно, данные таблицы 4,1, полученные по формуле Вейбулла, должны быть дополнены поправкой (4,21) на специфическое влияние ячеистой структуры.
Справедливость допущения (4,23) можно проверить сопоставлением расчитанных для разных при фиксированной толщине А по формуле (4.21) и измеренных опытным путём значений прочности, например, для ППУ-Э-25-3,2 (рис.4.16). Из рис.4.16 видно, что расчётное значение прочности сильно зависит от величины параметра о/ , При этом опытное значение прочности совпадает с расчётным при =0,5 и, следовательно, подтверждается выполнение равенства (4.23).
Полученные результаты показывают сильное влияние масштабного фактора образца и разрушения тяжей в поверхностном слое на результаты испытаний. Поэтому широко используемые в литературе /4, 24, 48, 51/ данные о сильном влиянии размера ячеек на прочность ППУ, полученные на стандартных образцах, недостаточно корректны, так как при этом не учитывается упомянутый выше эффект.
Таким образом, выполненные статистические исследования разрушения эластичных пенополиуретанов позволили определить степень пов - реждённости образцов перед их разрушением, выявить виды распределения прочности ППУ. Установлен закон влияния масштабного фактора образцов на прочность эластичных неноматериалов, в общем, противо-
199 -
Положный полученному Вейбуллом для монолитных материалов.