СТРУКТУРА И СВОЙСТВА ГАЗОНАПОЛНЕННЫХ ПОЛИМЕРОВ
РАСЧЕТ ДИАГРАММ СЖАТИЯ ЭЛАСТИЧНЫХ ПЕНОПЛАСТОВ С УЧЕТОМ КАЖУЩЕЙСЯ ПЛОТНОСТИ, СТЕПЕНИ ЗАМКНУТОСТИ ЯЧЕЕК, НЕОДНОРОДНОСТИ МАКРОСТРУКТУРЫ, РЕЛАКСАЦИОННЫХ СВОЙСТВ ПОЛИМЕРА — -0СН0ВЫ
- 165 -
Одно из наиболее широких применений при исследовании деформативности пенопластов получило эмпирическое соотношение Раша между сжимающим напряжением 6Г и деформацией С /53/:
<о = Е г(6) ; (4.1)
Где: Е^ - начальный модуль упругости пенопластов при сжатии; Г(£) - функция, которая по мнению Раша зависит только от геометрических параметров ячеистой структуры.
Несколько видоизменённое полуэмпирическое уравнение в сравнении с (4.1) получено Рашем позднее /54/ для диаграмм сжатия закры - топористых пенопластов.
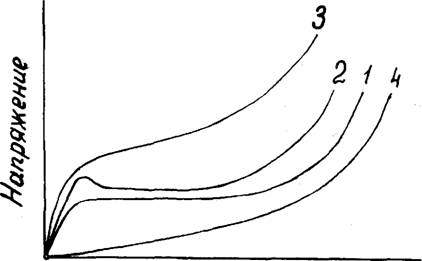
Уравнение (4.1) позволяет довольно полно описать экспериментальные данные по сжатию различных пеноматериалов, однако совершенно не объясняет специфику деформативности ячеистых материалов. Действительно, имеется несколько основных типов диаграмм сжатия эластичных пенопластов низкой кажущейся плотности, которые представлены на рис.4,1 /3, 4, 25, 53-54, 89/. Как следует из уравнения (4.1), вид диаграммы сжатия на рис.4.1 не будет меняться при не* изменной ячеистой структуре. В действительности при неизменной ячеистой структуре (у одних и тех же образцов эластичного ППУ) при температуре 293К может наблюдаться диаграмма сжатия типа 2, а при повышенных температурах - типа I. Более того, даже при одной и той же температуре вид диаграммы сжатия одних и тех же образцов эластичного ППУ может измениться с типа 2 (при повышенных скоростях деформации) до типа I при пониженных скоростях деформации /I/.
По этой же причине определяемая эмпирически функция деформации в формуле (4.2), предложенной Гентом и Томасом /86-88/:
(4.2)
|
Со «Е^./Сб') |
|
F /(I } |
Где: деформация; - отношение толщины тяжа к его длине; характеризует не только деформативность ячеистой структуры, но и
|
|
|
|
Рис. 4.1. Основные типы диаграмм напряжение-деформация при сжатии эластичных пенопластов. Цифры у кривых - тип диаграммы.
|
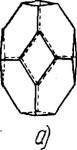
Рис. 4.2. 14-гранная модоль ячеистой структуры пенополимеров (а) и схема расположения тяжей при образовании макроячеек (б). |
Влияние релаксационных свойств полимера-основы. Поэтому рассмотрим теоретическое определение диаграмм сжатия пенополимеров.
В основу расчётов лёгких пенопластов положена предложенная нами /160/ 14-гранная модель ячейки пенопласта, представленная на рис.4.2. Ячеистую структуру этого типа образуют стержни шириной соеди
Нённые в квадраты. При этом все соседние квадраты соединяются друг с другом по углам во взаимно перпендикулярных плоскостях. У анизотропных пенопластов ячейки вытянуты в направлении вспенивания. Предполагаем, что стержни квадратного сечения жестко заделаны концами в недеформируемые узлы объёмом
Так, что высота узла значительно меньше длины стержней. Допускаем, что и при малых и при больших деформациях тяжи работают в режиме продольно-поперечного изгиба гибких стержней, причём при достижении критической нагрузки при сжатии реализуется энергетически наиболее выгодная форма потери устойчивости тяжей. Следствием упомянутых гипотез является, из учёта неразрывности структуры, необходимость при разрушении пенопласта коллективной потери устойчивости стержней, входящих своими концами в один узел. В качестве структурного фрагмента взят отдельный тяж, который заменён идеализированным расчётным элементом в виде прямого полимерного стержня с защемлённым концом с одинаковым по длине поперечным сечением. Если принять, что относительное изменение расстояния между соседними узлами газостр^к- турных элементов равно средней деформации пенопласта, то можно вычислить напряжения, действующие по концам рассматриваемого элемента и, далее, усреднённое напряжение для соответствующего однородного пенопласта.
Более детальное рассмотрение особенностей работы тяжей не меняет общей картины характера их деформирования, а потому является непринципиальным в поставленной проблеме. Количественный расчёт диаграмм сжатия I, 3, 4 типов лёгких однородных эластичных пенопластов был выполнен нами /160/ с использованием метода упругих параметров
Выражение (4.3) является обобщенной формулой диаграмм сжатия однородных пенопластов с учётом раздельного влияния как свойств полимера-основы (учитывается модуль упругости полимера-основы), так и свойств деформативности собственно ячеистой структуры (учитывается остальными членами формулы 4.3). Проверка показала в ряде случаев удовлетворительное соответствие результатов расчёта экспериментальным данным для эластичных пенопластов типа пенополивинилхлорида и пенополиэтилена /160/. Однако реальные системы пенополимеров являются часто более сложными и поэтому требуют более подробного анализа,
С учётом выполненных расчётов рассмотрим влияние других факторов на диаграмму сжатия пенопластов, рассмотренное нами в рабо-
Те /152/.
Предположим, что пенопласт является неоднородным и имеет некото» рый спектр распределения жесткости по слоям образца. Причиной такей неоднородности может быть распределение коэффициента формы тяжей ячеек по слоям, распределение по кажущейся плотности, неоднородность по модулю упругости полимера-основы и т. д., что не принципиально с точки зрения постановки задачи. В этом случае при сжатии образца в закритической области будет сжиматься вначале наиболее слабый слой, затем последовательно более жесткие слои материала. Экспериментально это наблюдается часто /I/.
|
|
Поскольку напряжение сжатия для всех слоёв такого образца будет одно и то же, а деформация образца суммируется из деформаций отдельных слоёв, диаграмму сжатия неоднородного пенопласта можно представить в виде: г^' -Г-
( 4.4 )
I n--i
|
|
П -{
Где: <э'~ напряжение сжатия неоднородного образца пенопласта, рж ное напряжению сжатия для каждого слоя с однородной структурой;
|
<5ГП |
S - общая деформация сжатия неоднородного образца пено
Пласта; д/
H-пГ —jf------ ^L^a ' ------------ толщина /1-го однородного
Nz* у" слоя образца;
£п~ £ - деформация /г-го однородного слоя образца; /? - порядковый номер слоя образца с однородной структурой;
H-Zh
П - общая толщина образца в недеформированном
П-1
Состоянии.
Значения б'и £ в (4.4) для каждого однородного слоя выражаются формулой (4.3), а определяется неоднородностью пенопласта (спектром распределения слоёв Я/t по жесткости).
Проведём численный расчёт диаграмм сжатия неоднородного пенопласта на примере эластичного пенополиуретана ППУ-75 кажущейся плотности = 45 кг/м3. Численное решение уравнения (4.3) для такого однородного слоя ППУ в приведенных координатах
- /(£) ( 4.5)
Где: Окр - критическое напряжение на диаграмме сжатия, соответствующее пересечению касательных в месте первого перегиба;
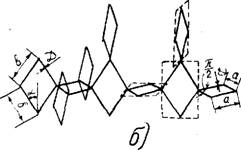
Выполнено нами в работе /160/. Гистограмма распределения критических напряжений для слоев неоднородного образца ППУ-75, полученная нами ранее /155/, представлена на рис. 4.3.
С помощью (4.5) легко получить в абсолютных координатах расчётную диаграмму сжатия для каждого однородного слоя:
6" = f{Јj; (4.6)
|
|
Рис, 4,3. Гистограмма распределения критической нагрузки элементов структуры ППУ-75 при первом цикле сжатия, совмещенная с графиком нормальной плотности вероятности.
|
|
Тии ^однородного пенопласта типа ППУ-75.
Для перехода от (4.5) к (4.6) использован спектр распределения, представленный на рис. 4.3.
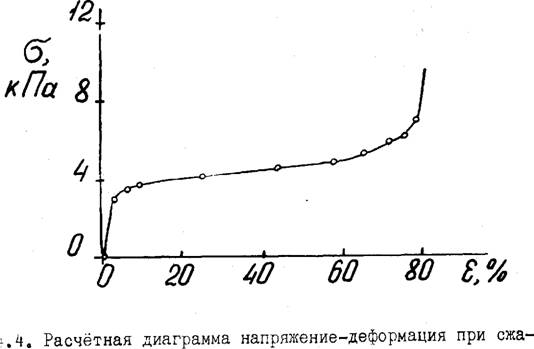
Подставляя расчитанные по гистограмме на рис, 4.3 величины толщины однородных слоёв образца h^ и численные решения (4.6) для этих слоёв в формулу (4,4), получаем для всего неоднородного образца диаграмму сжатия, представленную на рис, 4,4,
Из рис. 4.4 видно, что неоднородность пенопласта меняет вид диаграммы сжатия образца. Так, если у однородного образца наблюдаем ся диаграмма сжатия I типа (рис. 4,1) с чётко выраженным плато на 2-м участке, то у неоднородного образца (рис,4,4) наблюдается диаграмма сжатия 3 типа с существенным ростом напряжения на 2-м участке диаграммы. Сопоставление с прямым опытом, выполненное нами в работе /155/, даёт совпадение расчётной и экспериментально полученной диаграмм. Это вполне естественно, поскольку использованный в модели спектр распределения жесткости фрагментов газоструктурных элементов (рис. 4.3) расчитан нами из экспериментально снятой диаграммы сжатия.
Важно оценить также влияние релаксационных свойств полимера - - основы на диаграмму сжатия пенопласта. В общем виде эта зависимость учитывается через релаксационный модуль упругости Е в формуле (4.3). Проведём численный модельный расчёт диаграммы сжатия на примере однородного пенопласта типа ППУ-Э-35-0,8 /152/.
Ход релаксации напряжения у ППУ хорошо описывается уравнением Кольрауша. В частности, для ППУ-Э-35-0,8 зависимость релаксационного модуля упругости Е(t ) при деформации, соответствующей (э ,
Кр
Была выражена в виде:
T К ^ ( )
Е (£) = Е^ + Е0. е ТР ; (4.7)
Где: Е^= 0,0796 Ша - равновесный модуль упругости;
EQ = 0,0608 МПа - постоянная;
= 291 с - время релаксации;
F
К = 0,2667 - показатель степени;
T - время в с.
Испытания ППУ в режиме релаксации напряжения проводили при температуре 298К на испытательной машине "ИНСТРОН" по методике, описанной в /I/. Обработку кривых проводили на ЭВМ "МИНСК-32". Расхождение данных между опытной и расчётной кривыми не превышало 2$.
После подстановки значения Е (t) из (4.7) в (4.3) были получены расчётные диаграммы сжатия ППУ при различных скоростях сжатия. При этом время t в формуле (4.7) расчитывали из зависимости:
/ =--- §1-- ; (4.8)
V
Где: £ - деформация образца;
Скорость деформации образца.
Для удобства анализа полученные расчётные диаграммы представлены на рис.4.5 в приведенных координатах. Модуль "мгновенной" упругости при расчёте СО составил Е| = Е <?0+ Eq,
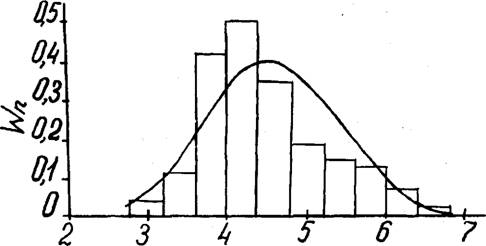
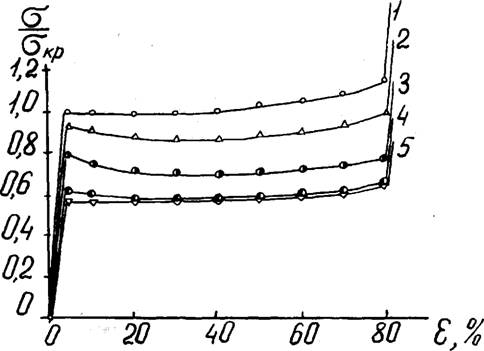
Из рис.4.5 (кривая I) видно, что для однородного пенопласта в условиях "мгновенного" нагружения характерна диаграмма сжатия 1 типа. Однако, для скоростей деформации ППУ от 1,Ь мм/с до 0,00016 мм/с характерны расчётные диаграммы 2 типа с чётко выраженным максимумом на 2-м участке кривых (кривые 2-4 на рис. 4.5). Для условно-равновесного сжатия (кривая 5 на рис.4.5) характерна диаграмма сжатия I типа. Из рис, 4.5 также видно, что с увеличением скорости деформации жесткость образцов увеличивается. Величина максимума на втором участке кривых оказалась наибольшей ~ 9,0$) при
У
Скорости деформации 0,016 мм/с. При увеличении скорости деформации до 1,6 мм/с величина этого максимума снизилась до 5,5$, а при снижении скорости деформации до 0,00016 мм/с величина максимума снизилась до 3,5$. Обсуждаемые особенности деформативности наблюдаются и при получении опытных диаграмм сжатия ППУ /I/, Однако, на
|
Рис. 4.5. Расчётные диаграммы напряжение-деформация при сжатии однородного пенопласта ППУ-Э-35-0,8. Скорость сжатия: I - "мгновенное" сжатие; 100 (2); I (3); 0,01 мм/мин (4); 5 - условно-равновесное сжатие» |
- 175 -
Практике наблюдается обычно совокупное влияние исследованных в работе факторов: кажущейся плотности пенопластов, степени замкнутости ячеек, однородности пеноматериала, модуля упругости полимера-основы, поэтому расшифровка деформативности представляется наиболее целесообразной с учётом выполненных расчётов.
Из представленных расчётов также следует, что с методической точки зрения при оценке однородности пенопласта наибольший интерес представляет определение спектра распределения из условно-равновесных диаграмм сжатия, так как при этом получаемое распределение не осложнено влиянием релаксационных свойств полимера-основы.
Таким образом, представленные теоретические расчёты впервые позволили объяснить физические особенности деформативности эластичных пенопластов, связанные с влиянием макроструктуры и свойств полимера-основы. Полученные данные позволяют установить способы регулирования свойств пеноматериалов при сжатии за счёт направленного изменения его макроструктуры в случае разработки новых пеноматериалов с повышенными эксплуатационными характеристиками. В то же время видна несостоятельность широко распространённой до последнего времени интерпретации деформативности в эмпирических уравнениях Гента и Томаса (4.2) и Раша (4.1) через функцию деформативности макрострзк» туры fit') и /^(£). Это связано с тем обстоятельством, что f (£) и F(£) связаны с одновременным наложением функции влияния макроструктуры и свойств полимера-основы.