СТРУКТУРА И СВОЙСТВА ГАЗОНАПОЛНЕННЫХ ПОЛИМЕРОВ

РАСЧЕТ ДИАГРАММ РАСТЯЖЕНИЯ ЭЛАСТИЧНЫХ ПЕНОПЛАСТОВ

Ранние попытки теоретического рассмотрения деформационных свойсте пенопластов /86-89/ позволили объяснить лишь некоторые особенности механического поведения вспененных пластмасс, поскольку предложен­ные авторами 6-гранные модели ячейки недостаточно полно отражают ре­альный характер работы элементов ячеистой структуры /160/. Поэтому позднее /160, 224/ нами была предложена 14-гранная модель ячейки пенопластов (рис. 4.2), которая довольно близко отражает реальную макроструктуру этих материалов. Отличительным признаком её являет­ся возможность изгиба всех силовых тяжей даже в случае малых наг­рузок при деформации образца в различных направлениях по отноше­нию к направлению вспенивания.

Ниже представлены результаты расчёта /225/ диаграммы растяже-
- 184 -

Ния пенопластов на основе предложенной 14-гранной модели ячейки (рис.4.2). Режим работы тяжа из условия симметрии нагрузки и кон­струкции ячейки сводится при симметричном изгибе к двум одинако­вым задачам продольно-поперечного изгиба стержня под действием'си­лы Р, приложенной к концу стержня, а упругая линия тяжа длиной 8- = 2.2 разбита на 2 участка, симметричных друг с другом как по кон­струкции, так и по нагрузке.

Расчёт перемещений тяжей, соответствующих начальному участку диаграммы растяжения, выполнен на основе разработанной в /222/ те­ории плоского изгиба брусьев малой жесткости при наличии произ­вольно большого упругого искажения их первоначального очертания, когда величина упругих перемещений изгиба может быть сравнима с длиной всего бруса. В этом случае выполненные нами расчёты /225/ по­зволили выразить растягивающее напряжение на начальном участке ди­аграммы в виде:

^ Гяч 2Р 2fi А Е

6-------------- —— - —-------------- г - --—1—Г ; ( 4.14)

Пп

(4<§+22>)2 <?2(2+ /р»2 3(2 + Д)2

А деформация пенополимера составляет:

-~7Г~ | (I + ^ - >-

+--- —

П 2

Где:/- - сила растяжения ячеики;. ' яч

<Ош - напряжение при растяжении пенопласта, расчитанное на

__ первоначальное сечение образца;

РТг7

---- силовой коэффициент подобия;

Н = EI - жесткоежь тяжа; / =2) /12 - момент инерции сечения тяжа;

Ширина тяжа; 8-2 Е - начальная длина тяжа; ^пп *" относительная Деформация пенопласта;

£ - величина £пп, соответствующая точке сопряжения начального и конечного участков диаграммы растяжения в месте перегибу: угол наклона линии действия силы Р; к, уо - эллиптические параметры; причём параметр макроструктуры = при каяущейея плотности

Пенопласта и плотности полимера-основы J^j определяется из ге­ометрических рассмотрений макроструктуры ячейки:

Гт г {г fi2T ■

—L_ = ----------- 1- ; С )

Fii ( 2 + fi^

Таким образом, уравнения (4.14), (4.15) теоретически описыва­ют в параметрическом виде начальный участок диаграмм растяжения однородных пенопластов. В то же время при £ > £с тяжи окажут­ся ориентированными в направлении приложения нагрузки, в результа­те чего модель ячеистой структуры окажется трансформированной. По­этому теория гибких стержней при дальнейших расчётах деформатив­ности пенопласта оказывается неприменимой. Однако, используя транс­формированную модель и выполнив условие сопряжения начального и последующего участков диаграммы растяжения, можно приближенно вы­полнить дальнейшие расчёты (для £пп > £ ).

Расчёты дают значение деформации пенопласта в месте, соответ­ствующем точке сопряжения участков диаграммы, £ ^20%, Опытным путём оно было уточнено и оказалось равным х.15% для эластичных пенопластов с объёмным содержанием полимера-основы s: 5$. Этому значению £ соответствует смещение полюса второго участка диаг - раммы относительно её начала на ~ 7%, поскольку ориентированные тяжи в начальном состоянии трансформированной макроструктуры уже находятся в напряженном состоянии.

Тогда с учётом (4.14), (4.15) и оговоренных условий работы элементов структуры в пересчёте на первоначальное сечение образца уравнение диаграммы растяжения трансформированной модели при

- 186 -

Р Р можно записать: спп ^

К J± = бгпо| с 4.17)

£п0 3 Яг I4 Спп tп 3 Рх

Где: £п - смещение полюса, равное значению £пп при экстраполя­ции к нулевой нагрузке линейного участка диаграммы растяжения в месте первого перегиба; £по - относительная деформация полимера-основы; (Эпо - напряжение при растяжении полимера-основы, расчитанное

На первоначальное сечение образца; 0'пп - напряжение при растяжении пенопласта, расчитанное на

Первоначальное сечение образца. Таким образом, имея диаграмму растяжения полимера-основы

Б-™ =

И подставляя значение функции ( 6 ) в (4.17), получим уравне­ние диаграмм растяжения пенопластов для £ пп ;> £с.

Была выполнена экспериментальная проверка результатов расчёта диаграммы растяжения открытопористого эластичного пенополивинил - хлорида марки "винипор эластичный" /225/. На рис.4.10 представле­на диаграмма растяжения плёнки пенополивинилхлорида. Для него было

О

Найдено: = 1030 кг/м ; Е = 4,97 Ша. Используя эти данные и ди­аграмму растяжения поливинилхлорида, по формулам (4.14 -4.18) была расчитана диаграмма растяжения пенополивинилхлорида с кажущейся плотностью = 80 кг/м3. Результаты расчёта и опытные данные представлены на рис. 4.10. Из рисунка видно, что соответствие ре­зультатов расчёта опытным данным - хорошее.

Удовлетворительное соответствие расчётных и опытных данных по­лучено нами /225/ также при испытании эластичного ППУ на основе сложных полиэфиров ( 30 кг/м3). Смещение полюса в этом случае

Составило <?п= 6...8%, а деформация в месте сопряжения участков в

ВпоМПа

О кО SO 120

Q !

О To 20 30 6nn%

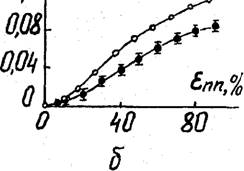
Рис. 4.II. Диаграммы растяжения жесткого пенополиуретана ППУ-3, полученные опытным путём для различных образцов; О - ^ = 31 кг/м3, Уо— = А - Jfj. 36 кг/м3,

- 188 -

Точке перегиба на диаграмме находилось в пределах £ = 14...18$.

Учитывая специфику растяжения стенок ячеек в процессе испыта­ния образцов закрытопористых пенопластов, можно было ожидать у них уменьшение обнаруженного нами эффекта /S-образного перегиба на начальном участке диаграммы. Поэтому были дополнительно испытаны образцы жесткого пенополиуретана марки ППУ-3 с различной степенью замкнутости ячеек. Испытания проводили на образцах в форме двой­ной лопаточки длиной 200 мм. Автоматическую запись диаграммы рас­тяжения выполняли на разрывной машине "ЙНСТРОН" с постоянной ско­ростью деформации образца 0,00083 при закреплении экстензо - метра на базе 50 мм.

На рис.4.II представлены результаты испытаний на растяжение жесткого пенополиуретана ППУ-3. Из риа 4.II видно, что жесткие пе­нопласты обнаруживают некоторые особенности при растяжении в срав­нении с эластичными материалами. Так, у образцов закрытопористого материала, как и ожидалось, эффект /^-образного перегиба на на­чальном участке диаграммы растяжения оказался почти полностью вы­рожденным. Однако и у открытопористого ППУ-3 смещение полюса (f и сопряжение при <fnn = £с оказалось хотя и достаточно чётко выраженным, но соответствовало значительно меньшим деформациям, чем у эластичных пенопластов. Это вызвано, вероятно, меньшей гиб­костью тяжей у жестких пенопластов, а также большей нелинейностью диаграммы растяжения монолитного материала при сравнительно не­больших деформациях. В результате наблюдается компенсация и перекры­тие части вогнутого участка выпуклым в месте

S-0 бразного пере­гиба на диаграмме.

Позднее /40, 226/ этот вывод был экспериментально подтверж­дён и для других жестких ППУ: начальный модуль упругости Е на первом линейном участке ниже, чем модуль упругости Ej на втором начальном линейном участке диаграммы растяжения лёгкого пенопласта.

- 189 -

Таким образом, выполненные измерения показывают, что в то вре­мя как монолитные полимеры имеют выпуклую форму диаграммы растяже­ния на начальном участке, соответствующие лёгкие пеноматериалы име­ют fS-образный начальный участ^ок. Аномальный вогнутый начальный участок имеет протяженность до по деформации образца пеноплас­

Та и вызван изгибными деформациями тяжей. При дальнейшем растяже­нии пеноматериала диаграммы вспененного и монолитного образцов имеют одинаковый характер. В результате на основе расчётов предло­женной 14-гранной модели ячейки можно количественно определить за­висимость напряжения при растяжении образца пенопласта от деформации.