СТРУКТУРА И СВОЙСТВА ГАЗОНАПОЛНЕННЫХ ПОЛИМЕРОВ

ОДНООСНОЕ СЖАТИЕ

В ещё большей мере, в сравнении с режимом растяжения, проявля­ются особенности разрушения пенополимеров в условиях одноосного сжатия.

Выполненные нами исследования показали, что характер деформации

И разрушения пенопластов определяется как строением и физическим состоянием полимера-основы, так и спецификой работы элементов мак­роструктуры при нагружении /159/. С учётом изложенного была предло­жена классификация основных видов диаграмм сжатия образцов, харак­терных для жестких пенопластов (рие.3.1б).

Оказалось, что у лёгких пенопластов с объёмным содержанием поли - мера-основы менее 30$ (рис,3.1 б а-в) наблюдается разрушение ячеис** той структуры за счёт потери устойчивости тяжей при достижении разрушающего напряжения при сжатии (6^)» У крупнопористых жест­ких пенопластов происходит сначала разрушение тяжей наиболее ослаб*» ленного слоя приблизительно на высоту одной ячейки (а) с одновре»

Ш ш В

-w

(о, МПа 9$

ЪП$ о 20 40 Q 20 W 0 20 V 0 20 W А) г'% 5) 61 е<% г) £'% д) '%

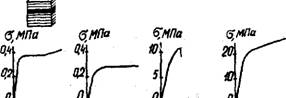
Рис. 3.16. Характерные виды разрушения ячеистой структуры пено* пластов при одноосном сжатии. На рисунке обозначены: а - пено- изовинил, it = 62 кг/м3; б - ППУ-3, 49 кг/м3; в - винипор полужесткий, )f~= 128 кг/м3; г - пенополиэпоксид ПЭ-5, 410 кг/м3; д - ППУ-3, 560 кг/м3.

Менным снижением напряжения. Б дальнейшем последовательно и необ* ратимо разрушаются тяжи каждого соседнего прилегающего слоя. У мелкопористых лёгких пенопластов также вначале наблюдается смятие наиболее ослабленного поперечного слоя, но на высоту не одной, а нескольких ячеек (б), Б дальнейшем этот слой расширяется за счёт смятия прилегающего слоя. На диаграмме сжатия этот участок харак­теризуется наличием плато, либо слабым увеличением напряжения при дальнейшем сжатии образца. После снятия нагрузки и длительного отдыха при повышенной температуре образцы, как правило, восста­навливают свои первоначальные размеры, У крупнопористых полужест­ких пенопластов при достижении (51™. наблюдается изгиб и смятие

Сж

Тяжей наиболее ослабленного слоя приблизительно на высоту одной ячейки (в). В дальнейшем последовательно сминаются тяжи каждого соседнего прилегающего слоя. На диаграмме сжатия этот участок также характеризуется наличием плато, либо слабым увеличением напряжения при дальнейшем сжатии образца. После снятия нагрузки и длительного отдыха при температуре 293К образцы практически полностью восстанавливают свои первоначальные размеры. Во всех случаях (а-в) поперечные размеры образцов заметно не меняются да*» же при деформациях сжатия до

Иначе ведут себя при одноосном сжатии пенопласты повышенной плотности. Хрупкое разрушение образцов происходит с образованием трещин по наклонным и продольным плоскостям (рис. ЗДбг). В слу­чае сжатия ППУ (рис,3,1бд) напряжение непрерывно возрастает даже после достижения (5СЖ* В то же время площадь поперечного сечения образца несколько увеличивается и сам образец принимает бочкооб­разную форму. Одновременно происходит смятие ячеек пенопласта,

Таким образом, у лёгких жестких пенопластов на диаграмме сжа­тия, как правило, наблюдается 3 четко выраженных участка: крутой начальный участок; снижение напряжения, плато, либо небольшой рост напряжения на втором участке; третий участок сильного возрас­тания напряжения. Начальный участок отражает сжатие и изгиб тяжей и стенок ячеек пенопласта до достижения ими потери устойчивости; на втором участке тяжи теряют устойчивость и разрушаются либо из­гибаются за счёт вынужденноэластической деформации, что приводит к резкому снижению напряжения в первом случае и возникновению плато или некоторому росту напряжения во втором; на третьем участке происходит окончательное смятие разрушенных ячеек и посте­пенный переход к сжатию полимера. Поведение пенопластов повышенной плотности при сжатии более близко к поведению монолитных пластмасс.

На диаграммах сжатия эластичных пенопластов можно выделить как правило 3 участка: крутой начальный участок, отражающий изгиб тяжей в докритической области; второй участок, соответствующий возникновению плато на диаграмме или незначительному росту напря­жения при больших деформациях образца (до 60$), отражает изгиб тяжей после потери ими устойчивости; третий участок, соответству­ющий дальнейшему значительному росту напряжения, отражает сжатие уплотнённых до взаимного соприкосновения тяжей. При увеличении жесткости ППУ при низких температурах более чем в 5 раз по сравне­нию с жесткостью при 293К вид диаграммы сжатия начинает меняться - появляется максимум при деформации сжатия Максимум имеет релаксационную природу и при снятии диаграммы в условно-равновес­ном режиме испытаний он исчезает /I/,

Исходя из геометрического рассмотрения элементов макроструктуры были определены основные особенности изменения прочности и модуля упругости при сжатии пенополимеров /135, 159/, Из условия общности механизма вспенивания и образования макроструктуры и подобного строения ячеек установлен принцип структурно-механической суперпо­зиции пенопластов, позволяющий указать эквивалентность изменения их прочностных и упругих свойств в широком диапазоне шкалы изме­
нения жесткости полимера-основы и кажущейся плотности пеноматериа* ла. Сформулированный закон эквивалентности заключается в следую­щем. Приведенный модуль упругоети Ед/Е (относительно модуля уп­ругости полимера-основы) при одноосном сжатии всех изотропных пе­нопластов одинаков для одной и той же приведенной кажущейся плот­ности j) (относительно плотности полимера-основы). Зависимость приведенного модуля упругости при одноосном сжатии от приведенной кажущейся плотности, расчитанная нами в работе /135/, для всех изотропных пенопластов описывается одним и тем же уравнением:

А*/Т „ У

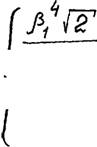
; при

TOC o "1-3" h z ЕП.) S+S1 - •

7") /За ^ (3-3)

; при —-—-— ^ -— ;

(1+ J3)2 я+fii

Где: fj и - параметры макроструктуры, определяемые из геомет­рических рассмотрений ячеек по формулам:

У" з/2+/3 ^ 3/27/2

I

$

F (I+/)3 Р (2,/J)2

T"^ кажущаяся плотность пенопласта;

_Р - плотность полимера-основы;

Еп - модуль упругости пенопласта при одноосном сжатии;

Е - модуль Юнга полимера-основы.

Приведённая прочность изотропных пенопластов при одноосном сжатиЕ Имеет одинаковый характер зависимости от приведенной кажущейся плотности и расчитывается /135/ по минимальному значению её вели­чины по формуле: л 0

Г г - г Fi2 С*

6п • о Г ; ПрИ ^о о ^ Ы —J

(I+J3)2 (I +/)2 432|/Р

Экспериментальное обоснование сформулированного принципа пред­ставлено на рис.3.17 и 3,18 /135/, Механические испытания пено­пластов проводили на испытательной машине "ИНСТРОН". На экспери­ментальную точку брали по 4 образца, что обеспечивало точность из­мерений до б% при доверительной вероятности 0,95.

Из рис,3.17 и 3,18 видно, что для всех изотропных пенопластов экспериментально обосновывается единая кривая зависимости приве­денного модуля упругости и прочности от приведенной кажущейся плот­ности. Характер представленной на рис.3.17 зависимости приведенно­го модуля упругости от приведенной кажущейся плотности показывает, что на начальном участке кривой ( 0 > f? Cj (%>)>• -0,2 ) жест­кость материала падает довольно резко. Это объясняется тем, что объёмная доля полимера в узлах ячеек при уменьшении отношения fyp уменьшается более резко, чем в тяжах. В то же время узлы представля» ют собой силовые элементы ячейки при сжатии в любом направлении, тогда как тяжи, расположенные в плоскости, перпендикулярной при­ложенной нагрузке, не являются таковыми. На втором участке С-0,2 ■> ^ (-0,55 ) ход кривой более плавный. При этом зависимость Еп/Е от ^/р приблизительно линейная. Это объясняет-» ся тем, что основна^цоля полимера в этом случае сосредоточена в тяжах и относительная площадь силовых тяжей в сечении ячейки, оп­ределяемая из (3.3), изменяется более плавно. На третьем участке кривой (fJ0<-O,55) характер зависимости приведенного модуля упругости от приведенной кажущейся плотности значительно меняется. Это вызвано тем, что здесь уже имеем дело с ячеистой структурой лёгких пенопластов, механизм деформирования которых сводится к изгибным деформациям тяжей, что резко снижает жесткость пенома­териала.

Следует отметить, что при оценке приведенной прочности прин­цип суперпозиции сформулирован в более общем виде, поскольку для

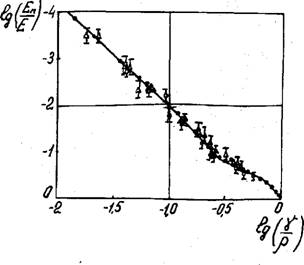
Рис. 3.17. Зависимость приведенного модуля упругости пено­пластов от приведенной кажущейся плотности в двойных лога­рифмических координатах. • - расчёт; О, □ , А, А - экс­периментальные данные для пенорезины, пенополивинилхлорида рецептуры винипор эластичный, жесткого пенополиуретана ППУ-3, пенополиэпоксида ПЭ-5 соответственно.

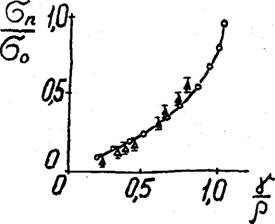
Р ис. 3.18. Зависимость приведенной прочности пенопластов при сжатии от приведенной кажущейся плотности. Обозначения: О - расчёт; А, А - экспериментальные данные для пенополиуре­тана ППУ-3 и пенополиэпоксида ПЭ-5.

Лёгких пенопластов параметр приведения связан с модулем упругости полимера-основы Е, но не с величиной (формулы 3,3 и 3.4).

Интересной разновидностью ячеистого строения пенопластов ока­залось обнаруженное нами впервые существование пенопластов с вза­имопроникающими ячеистыми структурами, когда наряду с ячейками полиэдрической формы в пенопласте одновременно присутствуют ячей­ки овальной формы /143, 144, 158, 196/, При этом структуры сущест­венно различаются линейными размерами ячеек и. их конфигурацией. В результате при образовании взаимопроникающих ячеистых структур на 2-3 уровнях прочность пенопласта может существенно увеличить­ся /143/,

Физический смысл установленного эффекта упрочнения пенопласта объясняется из анализа механизма деформации и разрушения лёгких пенопластов. Именно, у пенополимеров с полиэдрической формой ячеек низкие значения и Еп обусловлены повышенной деформативностью тонких тяжей при продольно-поперечном изгибе, в то время как у пенопласта с взаимопроникающими ячеистыми структурами овального типа величина (Эп и Еп существенно выше, так как у таких образцов отсутствуют гибкие элементы макроструктуры. С уменьшением кажущейся плотности пенополимера эффект упрочнения повышается.

Рассмотрим подробнее физические особенности кинетики деформа­ции и разрушения пенопластов /157/. Известно /9,10/, что деформа­ция полимерных материалов развивается с преодолением сил межмоле­кулярных взаимодействий и этот процесс связан с переходом через потенциальные барьеры в определённых активационных объёмах. Боль­шой вклад в изучение кинетики и природы вынужденно-эластической деформации дали представления о температурно-напряженной зависи­мости времени релаксации процесса /62/:

Где: Т - время релаксации; Q 0 - энергия активации; Т - температура;

Напряжение; fe - универсальная газовая постоянная; ^ и с/ - константы материала.

Если положить, что скорость деформации 6 обратно пропорцио­нальна времени релаксации, то из (3.5) можно получить зависимость предела вынужденной эластичности (5^ от температуры и скорости нагружения /62/:

£. £о ехр ( - ) ; (3.6)

В некотором интервале температур и скоростей эта зависимость подтверждена для многих полимеров /9, 63/. На примере пенополиуре­танов остановимся на физических особенностях кинетики деформации и разрушения жесткоцепных стеклообразных пенопластов.

Характерные диаграммы сжатия анизотропных ППУ низкой кажущей­ся плотности в стеклообразном состоянии представлены на рис.3*19* Из представленных диаграмм легко определить предел вынужденной эластичности образцов (эв. Данные на рис.3.19 показывают, что в случае сжатия образцов ППУ-3 низкой кажущейся плотности в направ­лении вспенивания после перехода через предел вынужденной эластичЬ ности на диаграмме наблюдается спад напряжения» Образующийся мак* симум можно объяснить одновременным действием двух факторов: во-пер* вых, нарушениями в структуре полимера-основы под действием напря­жения при пределе вынужденной эластичности /9/ и, во-вторых, пере­ориентацией тяжей с образованием "шейки" уплотнения. Перестройка макроструктуры из вытянутого по вспениванию ППУ расположения тяжей в уплотнённую макроструктуру с преимущественным расположением тяжей в перпендикулярном вспениванию направлении приводит к росту "шейки" уплотнения вплоть до полного перехода всех тяжей в эту зону при

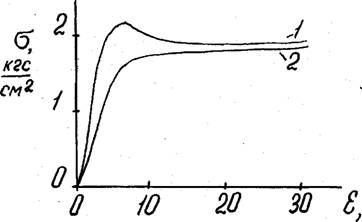
Рис. 3.19. Диаграммы сжатия ППУ-3 С F = 37 кг/м3) при 293К на образцах размером 50x50x50 мм в направлении вспенивания (I) и в направлении, перпендикулярном вспениванию (2).

Щ **'

Кгс

См2 3

2 1

0 .

-100 -50 О 50 /00 /50 Z°C

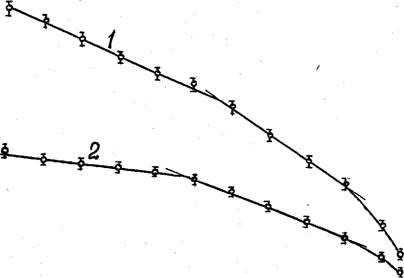
Рис. 3.20. Зависимость предела вынужденной эластичности ППУ-3 (L}f= 56 кг/м3) и ППУ-305А ( 2. <Г= 40 кг/м3) от температуры при 6 =0,0083 с"1.

Деформации сжатия «7Q$ и обеспечивает появление плато на диаграм­ме после снижения нагрузки. Подтверждением этого служат исчезно­вение максимума на диаграмме и отсутствие переориентации тяжей макроячеек при достижении (э в случае сжатия того же образца в направлении перпендикулярно вспениванию (рис.3.19). У пенопластов повышенной кажущейся плотности ( ^>200 кг/м3) характер диаграммы сжатия аналогичен наблюдаемому для монолитных полимерных материа­лов (рис.3,16). Таким образом, специфика перестройки макрострук­туры при деформации пенопласта является одним из условий появле­ния или отсутствия максимума на диаграмме сжатия.

Представленная на рис.3,20 зависимость предела .вынужденной эластичности при сжатии ППУ от температуры показывает, что у ППУ-3 при температуре 323К наблюдается излом (Тиз) зависимости ~ Т. Он находится существенно ниже температуры стеклования, измеренной дилатометрическим методом (Т = 393К). В работах /168, 198/ аналоги - чный релаксационный переход у ППУ-3 отмечен при изучении его ди­намических механических свойств. Учитывая микрофазное разделение в полиуретанах, эту область, вероятно, можно отнести к релаксаци­онным процессам в переходном состоянии между жестким и эластичным блоками, что и объясняет наблюдаемый переход.

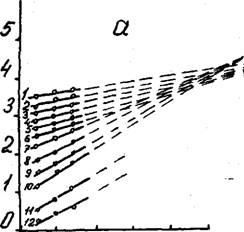
Приведенная на рис,3,21 зависимость (5^ - fy £ даёт для ППУ - -3 в некотором интервале температур (ниже Т ) два веера отрезков прямых. Это позволяет стеклообразное состояние у ППУ-3 разделить на два подсостояния, что характерно /9/ для монолитных полимеров с широким интервалом Т,..Т. Поскольку деформация полимеров

О х и

Связана главным образом с преодолением барьеров межмолекулярного взаимодействия (ММВ), а величины Ј? Q, £ , </ в (3,6) характеризу­ют кинетические параметры процесса, рассмотрим их определение.

Данные рис,3,21а показывают, что полюсу соответствует значение Рд €0 -8 для интервала температур 323...393К и =11 для интер­вала температур 2I3...323K, Поскольку значение полюса связано с

/CSC См2

-V О г * 6

8 Ш 12 (С)

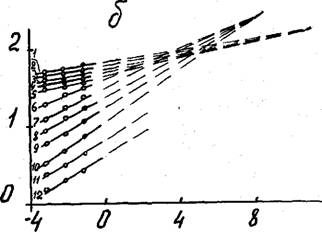
Рис. 3.21. Зависимость предела вынужденной эластичности ППУ-3 ( а, ^ 56 кг/м3) и ППУ-305А (б. ^ 40 кг/м3) от скорости деформирования при температурах Т = 213 (I), 233 Ш7 25УТ5), 27Т С4), 293 С5),-31-3 (б), 333 (7), 353 (8), 373 (9), 393.(10), 413 (II), 423К (12).

4

12 FyЈCС'')

Размерами кинетических единиц, можно ожидать различие в значениях параметра dL, характеризующего размеры кинетических единиц. Расчё­ты показывают (табл.3.2), что для высокотемпературной области

Табл.3.2. Значения кинетических параметров деформации стек­лообразных ППУ.

ППУ к ia3_:i. f_.!o

"о" 00- ^, 2 ПРИ 2 ПРИ

М С~1 ккал ккал. мм__ 0 Q-I ккал ккал. мм^ 0 моль моль кгс ^ моль" моль кгс ^

ППУ-3 56 8 33 740 50 II 44 1010 20 78 8 34 467 50 -

ППУ-305А 40 8 33 1440 30 II 54 2360 20 50 8 32 927 30 -

Значения параметров при Тиз составили: Q = ЗЗккал/моль; 2

= . Качественно аналогичные зависимости получены для

ППУ-3 с другими значениями кажущейся плотности а также для ППУ на основе простых полиэфиров (рис.3.216, табл.3.2). Анализ по­лученных данных показывает, что часть параметров кинетики дефор­мации стеклообразных ППУ iQQ, определяющих скорость процесса, находится на уровне их значений для монолитных полимеров /199-2СШ)/. Это согласуется с общими представлениями о деформации как термо - флуктуационном процессе, скорость которого определяется выражени­ем типа (3.6), причём процесс деформации идёт с преодолением главным образом барьеров ММВ. Однако, значения параметра У - для взятых ППУ примерно на 3 десятичных порядка превосходят его зна­чение для монолитных полимеров. Поскольку вынужденно-эластическую

- 101 -

Деформацию монолитных полимеров можно уподобить /200/ вязкому те­чению олигомера, объём молекулы которого равен объёму кинетичес­кой единицы деформации d - , указанная интерпретация этого пара­метра для ППУ на первый взгляд представляется неопределённой и противоречивой (как из-за сильной зависимости d от, так и из - за исключительно большой величины параметра

Следует отметить, что обсуждаемые значения и для ППУ являются эффективными характеристиками пеноматериала, распростра­няемыми не только на полимер-основу (около 5% по объёму), но и на газовую фазу (около 95$ по объёму). Кроме того, и (5^ связаны с особенностями строения и деформирования элементов структуры ППУ (в данном случае с концентрацией напряжений при продольно-попереч­ном изгибе тяжей макроячеек в процессе одноосного сжатия образца пенопласта). Следовательно, при определении физических особенное» тей деформации пенопластов задача сводится прежде всего к уста­новлению фактического уровня напряженного состояния полимера в элементе структуры (э и фактического объёма кинетической едини­цы деформации полимера с/^.

Т т? . J при ^ ;

Г - - f -/ 2* fit 2 (I+уЗ)2 Р (2

(3.7)

Поскольку уровню одинаковой интенсивности напряжения полиме­ра в элементах ячеистой структуры соответствует одинаковый уро­вень нагружения образцов пенопласта относительно (эъ /169/, ис­пользуя выражение (3.3) легко выразить в параметрическом виде коэффициент перенапряжения в полимере макроячеек при одинако­вой интенсивности напряжения в образце пенопласта:

F/I'^ ^ J2

Е

£_ п и А(£> , T_ . З / Ti3.

(I +Р)2 при 2 "H " (I+/)2 А+ Pi'

- 102 -

Тогда величину можно представить в виде: а выражение (3,6) можно записать:

£ = fexp ( ) = £оехр ( ); (3.9)

R-T ВТ

4.6:-

Где:0*ви = - интенсивность напряжения в полимере-основе

При достижении (31 пенопласта,

Г)

Из (3,6), (3.9) видно» что значения параметров (J и f для полимера-основы и пенопласта одни и те же, то-есть характеризуют свойства полимера-основы. Однако параметр для пенополимеров яв­ляется эффективной величиной и расчитывается из (3.7), (3.8) как произведение его величины для полимера-основы на коэффициент пере­напряжения S" (определение по формуле (3,7) представлено на рис,3,17, либо можно использовать экспериментальные данные по за­висимости Е ^ от ^ ),

Сопоставление расчётных и опытных данных по определению пред* ставленное в табл,3,3, показывает их удовлетворительное соответствие,

Табл,3.3, Сопоставление расчётных и опытных данных для ППУ по определению параметра dC,

Эксперимент Расчёт

ППУ Т, К б, ——

TOC o "1-3" h z кг_ ^» 2 ^ и* о о/т сСт Е vi 3 ккал Мм к кал, Мм - = —

М моль*кгс моль КГС. Е^Л.

ППУ-305А 303 40 1440 1,28

1,55 1,42

50 927 1,17

ППУ-3 323 56 740 1,38

1,60 1,9

78 467 1,65

- юз -

Значение параметра характеризующего объём кинетической единицы деформации полиуретана, близко к его значению для других полимеров /157, 199-200/ и несколько выше у ППУ-3 по сравнению с ППУ-305А. Из табл.3.3 также видно, что расчётные значения J.^ мало отличаются от опытных (не более 20$) и это указывает на удовлетворительное их соответствие.

Из рис.3.21 и табл.3.3 видно, что при рассмотрении кинетики де­формации ППУ ниже Тиз наблюдаются качественно аналогичные резуль­таты, поэтому их более полный анализ не приводится. Выше 393К на рис.3.21 наблюдается параллельность отре! ков прямых (5^ - 6 $ Что позволяет представить эту зависимость в виде /199/:

. • Q .

£« £ ехр ( - — </б); (3.10)

0 R т

Различный характер кинетики деформации пенопластов выше и ниже 393К обусловлен, очевидно, различным механизмом релаксации полиме- ра-основы в этих интервалах температур.

Таким образом, представленные данные позволяют по результатам полимера прогнозировать зависимость предела вынужденной эластичнос­ти от температуры и скорости нагружения для различных пенопластов на его основе (в общем, для бесконечного множества пенопластов); по результатам испытаний пенопласта прогнозировать зависимость (о^ от Т и £ для монолитного полимера, а также других пенопластов на его основе; по результатам испытаний пенопласта оценивать кинетические параметры деформации полимера Q0* Это полезно, например,

При оценке структуры и кинетических параметров деформации полимера - - основы как на стадии разработки пенопластов с заранее заданными свойствами, так и при изучении структурно-механических свойств пе­нопластов при старении.

Научные результаты исследований, изложенных в настоящем разделе, заключаются в том, что определены основные виды разрушения и их ме**

- 104 -

Ханизм при одноосном сжатии пенополимеров; экспериментально обоснова­ны общие закономерности изменения приведенных упругих и прочностных характеристик в широком диапазоне шкалы изменения кажущейся плотнос­ти (принцип структурно-механической суперпозиции пенопластов); по результатам испытаний пенопластов предложен способ определения па­раметров кинетики деформации полимера-основы, а также прогнозиро­вания кинетических параметров деформации других пенопластов на осно­ве этого же полимера.