Строительные машины и оборудование

Расчет основных параметров режима работы дробилок крупного дробления

Дробление материала в ККД во многом аналогично дроблению в щековых дробилках, что позволяет использовать ранее изло­женную методику при определении технологических параметров режима работы конусных дробилок.

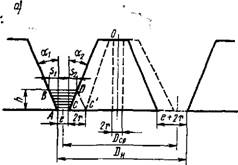
Угол захвата в конусных дробилках, равный углу между по­верхностями подвижного и неподвижного конусов, не должен превышать двойного угла трения, т. е. р=аі+а2^2ф (рис. 3.5,а). Обычно для ККД величина р=21 ... 23°.

Частота вращения эксцентриковой втулки определяется, как и для щековых дробилок, из условия свободного выпадения раз­дробленного материала за время отхода дробящих поверхностей друг от друга, т. е. материал должен пройти путь h за время I, равное половине оборота эксцентриковой втулки. Следовательно, h=gt*/2;

T = ylhfЈ= 1/(2 п),

Где п — частота вращения втулки, об/с. Из принятого условия следует

П= 0,5 У^Ш), (3.1)

Величина h определяется из схемы на рис. 3.5,а:

H= (Si + s2) I (tg аі +tg а2) =2г/ (tg а'і+tg а2), где si+s2 — величина отхода подвижного конуса от неподвиж­ного за одно качание, м; г — эксцентриситет качаний подвижно-

А — частоты вращения эксцентриковой втулки и производительности дробилки; б — мощности приводного двигателя

Го конуса, м (расстояние между осями дробилки и подвижного конуса); ai и аг — углы образующих неподвижного и подвижно­го конусов с вертикалью соответственно. Подставляя значение h в формулу (3.1), получим частоту вращения втулки (об/с):

П==0,2ЬУgiig^+igaJir^QJbV^ + tZ^lr. (3.2)

Учитывая торможение материала о стенки конусов при из­мельчении, полученное значение п обычно уменьшают на 10%.

Производительность ККД определяется объемом материала V, выпадающего из дробилки за один оборот эксцентриковой втул­ки, и частотой вращения втулки в рассчитываемое время. За один оборот втулки из дробилки выпадает материал, объем которого равен кольцу сечением ABDC (см. рис. 3.5,а):

V=*DC02e + si + s* h, Ср 2

Где Dcр — средний диаметр кольца щебня, м. Зная, что і'і+«2=2г и /i=2r/(tgai + tga2), получим объем ABDC (м3):

»<' + г> , (3.3)

Tg al + Ч «2

Производительность дробилки (м3/с): П={х«У, где — коэф­фициент разрыхления материала; п — частота вращения втулки, об/с. Подставив значение V из формулы (3.3), получим

П=2я£>срг (e+r) iwl (tg a'i+tg a2). (3.4)

Мощность двигателя дробилок ККД определяется на основа - вании теории Кирпичева — Кика по методике, изложенной выше при расчете мощности привода щековых дробилок. Согласно ей

(с учетом разработок проф. Л. Б. Левенсона) А—(VD — Vd),

2 Е

Где Vd — объем загружаемого материала, м3; Vd — объем готового продукта, м3.

VD 6 Д d 6 d

(рис. 3.5,6), где D и d — наибольшие диаметры кусков исходного материала и готового продукта соответственно, м; Dcр и dcp — средние диаметры загрузочного и разгрузочного кольцевых отвер­стий, м. Принимая £>Ср«dcp^DH (где DH — диаметр неподвижного конуса в нижней части), получим A=os2n2D„(D2—d?)/(2E) Дж, где ста — предел прочности дробимого материала, Па; Е — модуль упругости дробимого материала, Па. Отсюда мощность привода ККД (кВт)

N=сгв2яю/)н (D2—d2) / (24 • 103£), (3.5)

Где со — угловая скорость эксцентриковой втулки, рад/с. 44

Мощность привода ККД рассчитывают также по эмпирическим формулам. Наиболее часто пользуются формулой проф. В. А. Олевского:

N=60Kdn2m, (3.6)

Где К — коэффициент, учитывающий прочность измельчаемого ма­териала (для прочных пород К—24); dH— диаметр основания подвижного конуса, м; г — эксцентриситет качаний подвижного конуса, м; п — частота вращения эксцентриковой втулки, об/с. С учетом действия пиковых нагрузок (при пуске дробилки под за­валом) значение мощности (кВт) увеличивается в 1,5 раза, т. е.

NycT= 1,5N=2160dHVn. (3.7)

Мощность приводного электродвигателя ККД можно также опре­делить на основании действующих в ней нагрузок от усилия дроб­ления. При этом возникающие нагрузки от неуравновешенных масс эксцентрика и подвижного конуса не учитываются ввиду их незначительной величины по сравнению с нагрузками от усилия дробления.

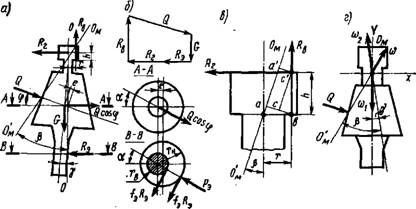
Расчетная схема нагрузок на подвижный конус и реакций его опор приведена на рис. 3.6,а, где Q — равнодействующая сил дробления материала, Н; G — сила тяжести подвижного конуса, Н; RB — вертикальная реакция в подвеске подвижного конуса, Н; Rr — горизонтальная реакция в подвеске подвижного конуса, Н; R3 — реакция в эксцентриковом стакане дробилки (Н), направ­ленная, как и Q, под углом а к плоскости эксцентриситета.

Все указанные на схеме силы в каждый отдельный момент ра­боты дробилки находятся в равновесии и поэтому должны состав­лять замкнутый многоугольник сил (рис. 3.6,6). Для преодоления

Всех сил сопротивлений, возникающих при работе дробилки от сил трения на опорах и от Q, на эксцентрике должен быть создан крутящий момент, равный сумме моментов:'

1. Момента трения в эксцентрике (Н-м) Мэ—}эЯэ(гв--гн), где /э — коэффициент трения скольжения на внутренней и внешней поверхностях эксцентрика; гъ и гя — соответственно радиусы внут­ренней и внешней поверхностей эксцентрика, м.

2. Момента горизонтальной составляющей равнодействующей сил дробления, приведенного к оси эксцентрика (Н-м) МДр= =Qcosq)esina, где <р — угол между Q и горизонталью, град; е — эксцентриситет вала конуса на уровне горизонтальной составля - щей Qcos<p, м; а' — угол между равнодействующей сил дробления и плоскостью эксцентриситета (обычно а=20...30°).

3. Момента трения в верхней подвеске от горизонтальной реак­ции, приведенного к оси эксцентрика (Н-м) Afr=fn#ra'c/<o/co2, где fa — коэффициент трения скольжения рабочих поверхностей верх­него подвеса; а'с'—расстояние от мгновенной оси вращения под­вижного конуса до точки приложения силы Rr, м; со — угловая скорость вращения подвижного конуса относительно мгновенной оси, рад/с; а>2 — угловая скорость эксцентрика, рад/с.

Из схемы на рис. 3.6,в видно, что а'с'—ас=аЪ—cb==r cos р— —h sin р, где г — расстояние от вертикальной оси до точки прило­жения RT, м; h — расстояние от точки подвеса до опорной шайбы, м; р — угол между вертикальной осью дробилки и мгновенной осью вращения подвижного конуса.

Угловая скорость движения подвижного конуса относительно мгновенной оси определится из уравнений проекций векторов уг­ловых скоростей на осях У и X (см. рис. 3.6,в) сої cos y=co2+ —j—со cos р и ©і sin y=co sin р, где у — угол между вертикальной осью дробилки и осью подвижного конуса. Решив эту систему уравнений, получим (o=co2/(sin р ctgv—cosp) и соответственно со/со2=1 /(sin р ctg y—cos р). Следовательно, момент трения от го­ризонтальной реакции (Н-м)

Л/Г — f Q т cos Р ~~ h sin Р г — /іЛп. о. о •

Sin р ctg y — cos Р

4. Момента трения в верхней подвеске от вертикальной реак­ции, приведенного к оси эксцентрика (Н-м); по аналогии с пре­дыдущим

М, = UR, ab

<о2 sin pcgt y — cos p

Где RB — вертикальная реакция в верхней подвеске, Н; ab— =rcosp — расстояние от мгновенной оси вращения до точки при­ложения RB.

Крутящий момент на эксцентрике (Н*м), необходимый для Преодоления сил Трения В опорах И усилия дробления, Мкр= =-Мэкс+Мдр+-Мв+Мг, а крутящий момент на валу двигателя ко­
нусной дробилки Муст—МКр/іц, где і — передаточное число приво­да дробилки, т} — КПД привода. Мощность двигателя (кВт)

Л/уст = Л1устП/1000,

Где п — частота вращения вала электродвигателя, об/с.