Строительные машины и оборудование
Основы теории процесса измельчения
Горные породы, подвергаемые измельчению, представляют собой сложные полиминеральные среды, в которых зерна отдельных минералов связаны между собой силами сцепления. Различают два вида сил сцепления — силы, действующие внутри зерен (внутри - кристаллические), и силы, действующие между зернами (межкристаллические). Наибольшее влияние на эффективность измельчения оказывает вторая группа сил, так как разрушение отдельных кусков происходит по наиболее слабым местам — плоскостям спайности. Значение этих сил определяется разнообразными факторами и не поддается точному определению. Кроме того, энергоемкость процесса измельчения в дробильных машинах зависит от размеров, формы и однородности кусков, их физико-механических свойств, влажности и т. д. Поэтому конечной целью теоретических исследований процессов измельчения является получение (в общем виде) зависимостей между расходуемой энергией и отдельными характеристиками измельчаемого материала.
Наиболее известными гипотезами, устанавливающими такие зависимости, являются теории дробления Риттингера и Кирпичева — Кика. Теория Риттингера (1867) устанавливает взаимосвязь между работой, затраченной на измельчение материала, и вновь образованной при этом поверхностью кусков, т. е.
A=kAS, (1.2)
Где А — работа, затраченная на измельчение, Н-м, k — коэффициент пропорциональности, Н/м; Д5 — величина вновь образованной поверхности, м2.
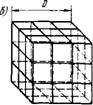
Экспериментального подтверждения данной гипотезы Риттин - гер не привел, но предложил методику определения величины вновь образованной поверхности. С этой целью измельчению подвергались куски кубической формы, разрушение которых происходило по взаимно перпендикулярным плоскостям. Обозначив длину ребра исходного куска через D и степень измельчения через і, получим: при 15 = 2 (рис. 1.3,а) кусок разделяется тремя взаимно перпендикулярными плоскостями. В результате деления получится 23=8 кубиков. Следовательно, вновь образованная поверхность AS=8-6(D/2)2—6D2=6D2 и может быть записана в виде AS=6D'2(ii—I). Работа измельчения As=k6D2(ii— И) = =ki(ii—I), при i=3 (рис. 1.3,6) кусок разделяется шестью взаимно перпендикулярными плоскостями. В результате деления по
лучается 33 =27 кубиков. Следовательно, вновь образованная поверхность A5=6(D/3)2-27—6D2= 12D2 и может быт£ записана в виде AS=6D2 (3— 1) =6D2 (t2—1). Работа измельчения А2 — — k6D2(i2—I) =ki(i2—1). Следовательно, при степенях измельчения in И im An=ki(in— 1); Am==ki(im—И). Отсюда An/An={in-l)/(tm~l). /
Пр^і больших степенях Измельчения (/>1) получим An/Am^in/im - При измельчении объема материала V (м3) в кусках, средневзвешенный размер которых DCB, число таких кусков равно V/Dzсв. Учитывая, что на
А)
Рис. 1.3. Схема разрушения куска по теории Риттингера: а —при (=2; б —при І-3
Разрушение одного куска затрачивается работа A = 6kD2cB(i—I), на измельчение V (м3) материала потребуется работа A=6kD2CB(i—l)/V/D3CB=6k(i—>l)V/DtB. Приняв плотность материала равной р (кг/м3)', на разрушение материала массой т (кг) затратится работа
. 6k і— 1 А =- т.
Р Ясв
Обозначив 6&/р через kд, получим зависимость, выражающую гипотезу Риттингера:
A—kR(i—l)tn/DCB. (1.3)
В этой зависимости затруднено определение лишь коэффициента пропорциональности kR, что снижает ее практическое значение.
Теория Кирпичева — Кика устанавливает зависимость между расходуемой на измельчение работой А и объемом V (массой т) разрушаемых тел.
В 1874 г. проф. В. JI. Кирпичев впервые сформулировал закон подобия для тел, находящихся в упругом состоянии, согласно которому
A1/A2=Vl/У2=тх/тг. '(1.4 J
В 11885 г. проф. Кик опубликовал работу, в которой закон подобия В. JI. Кирпичева был распространен на область пластических деформаций хрупких материалов, что вполне допустимо. Согласно ей работа, затрачиваемая на измельчение, A=cr2V/(2Е), где а — напряжение, возникающее при разрушении материала, Н/м2; V — объем измельчаемого куска, м3; Е — модуль упругости, Н/м2.
|
|
|
1 1 |
4ч |
|
—Х-- |
14 N |
|
"ч |
Учитывая, что физико-механические свойства конкретного материала являются величиной постоянной, закон„Кирпичева — Кика 16 ,
может быть записан в следующем виде:
A=kV. (1.5)
Согласно, этому закону работа измельчения одного куска кубической фо^мы с длиной ребра D равна A = kD3. При измельчении материала массой т и плотностью р в кусках крупностью DCB методика определения работы разрушения аналогична рассмотренной ранее в теории Риттингера. Следовательно, А = = kD2CBm/ (pDB)=km/P=kV.
Ввиду того что k/p для данного материала является величиной постоянной,
A=ktn. (1.6)
Общим недостатком рассмотренных теорий является то, что каждая из них учитывает лишь часть затрачиваемой в процессе измельчения энергии: первая — на непосредственное образование новых поверхностей, возникающих за пределом упругости (пластичности); вторая — на упругую деформацию измельчаемого материала. Поэтому в последующем было распространено мнение, что каждая из гипотез справедлива для различных стадий измельчения: теория Риттингера не учитывает затрат энергии на упругую деформацию материала и поэтому справедлива для процесса помола, где происходит интенсивное образование новых поверхностей; наоборот, теория. Кирпичева — Кика предполагает, что основная часть работы измельчения затрачивается на упругую деформацию материала, происходящую при дроблении.
Эти теории дополняют друг друга, так как в реальном процессе измельчения горных пород одновременно происходят процессы деформации материала и образования новых поверхностей. В 1940 г. П. А. Ребиндер предложил формулу расхода энергии при измельчении материала, которая объединяет рассмотренные выше теории:
A=klAV+k2AS, (1.7)
Где k и h2 — коэффициенты пропорциональности; AV — объем деформированного материала; AS — вновь образованная поверхность. Недостатком данной формулы является отсутствие методики определения коэффициентов k и fe2-
В 1951 г. Ф. Бонд выдвинул гипотезу процесса измельчения, в которой математически объединил теорию Риттингера и Кирпичева — Кика. Согласно Ф. Бонду, работа, необходимая для измельчения т (кг) материала со средней крупностью Dcp до средней крупности готового продукта dcp, выражается формулой
TOC o "1-3" h z A=kb(l/Vd;p-l/VD^m, (1.8)
Где — коэффициент пропорциональности.
В последующем зависимость Ф. Бонда была преобразована А. К Рундквистом:
A=kp[n~lm/Dcpn-1. (1.9)
2—5258 гт---------------------- -—"і 17
Подставляя в эту зависимость значения п, равные 1,5 и 1. можно получить выражения законов Риттингера, Бойда и Кир - пичева — Кика соответственно.
![]()
|
|
|
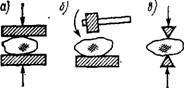
Рис. 1.4. Схемы воздействия внешних нагрузок на измельчаемый материал |
Анализируя рассмотренные гипотезы, следует обметить, что ни одна из них не является универсальной: одни учитывают расход энергии на преодоление упругих деформаций в материале (гипотеза Кирпичева— Кика), другие увязывают расход энергии с конечными результатами процесса — степенью измельчения (гипотезы Риттингера и Бонда). Условностью рассмотренных гипотез является исследование процесса разрушения тел правильной геометрической формы под действием равномерно распределенных сжимающих нагрузок. Однако, как показывают многочисленные исследования процесса измельчения, в дробильно-помольных машинах разрушение материала происходит под действием сосредоточенных нагрузок, что значительно меняет ход процесса. В связи с этим непосредственное использование гипотез измельчения для технико-экономического и конструктивного расчета дробильно-помольных машин весьма затруднено и требует введения поправочных коэффициентов, получаемых, как правило, экспериментально.