СТРОИТЕЛЬНЫЕ КОНСТРУКЦИИ С ПРИМЕНЕНИЕМ ПЛАСТМАСС
Особенности расчета гибких трехслойных панелей со сплошным средним слоем
Для ограничения прогибов, а также для уменьшения сжимающих напряжений от изгиба, которые могут вызвать потерю устойчивости обшивки, панели типа «сэндвич» с металлическими обшивками при
G
I рекомендуется закреплять по
Большой гибкости
Всему контуру (например, металлической раме) и рассчитывать их как гибкие пластины, с учетом цепных усилий, по приведенной ниже методике.
Условные обозначения. Геометрические параметры и физические характеристики материалов:
Ап, Ьп — размеры пластины-ячейки в плане в см;
D — изгибная жесткость пластины, определяемая по формуле (5.39);
F06P — площадь сечения обрамления пластины в см2;
J^ — момент инерции сечения обрамления относительно оси, параллельной срединной плоскости пластины в см4;
ЕобР — модуль упругости материала обрамления в кГ/см2; Внутренние усилия и напряжения:
Л4верт—изгибающий момент в обрамлении от внешней нагрузки в кГ • см;
Мтор—изгибающий момент в обрамлении от цепных напряжений в кГ • см;
N—продольная сила в обрамлении от цепных напряжений в кГ;
О1н—нормальные напряжения в верхней (наружной) и нижней (внутренней) обшивках в кГ/см2; — цепные напряжения в обшивках в кГ/см2.
Основные принципы расчета. Излагаемая ниже методика расчета основана на известной теории изотропных (однослойных) гибких пластин, но с учетом влияния податливости среднего слоя при сдвиге, жесткости опорного контура и обрамления пластины, при различном соотношении ее сторон [58, 112]. Проведенные исследования позволили установить расчетные зависимости между напряжениями и деформациями и различными видами нагрузок, действующих на гибкую пластину при ее функционировании в системе ограждающей конструкции. Разработана также методика расчета конструкций, включающих гибкие трехслойные пластины, на температурные воздействия [59].
|
Таблица 28 Предельные прогибы изгибаемых элементов
|
Расчет панелей, включающих гибкие трехслойные пластины, закрепленные по контуру, сводится к расчету самих пластин-ячеек на приложенную непосредственно к ним равномерно распределенную поперечную нагрузку и на усилия, возникающие при их работе в системе панели, а также к подбору (по прочности и жесткости) сечений элементов обрамления. Прочность и жесткость сечений элементов обрамления, работающих совместно с примыкающими участками трехслойной пластины, проверяют с учетом усилий, действующих как в плоскости пластины, так и из плоскости ее.
Гибкие трехслойные пластины, закрепленные по контуру, рекомендуется применять с металлическими обшивками толщиной не более 1 мм.
Опорный контур пластины можно считать жестким, если
Р гверт
Как самостоятельно (рис. 4.36), так и в системе панельных конструкций. Приведенные ниже формулы можно использовать также для расчета пластин-ячеек, свободно опертых по контуру (без закрепления); в этом случае следует принимать J обр =0.
Для прямоугольных пластин-ячеек, свободно опертых по всем кромкам на жесткий контур и загруженных равномерно распределенной нагрузкой (рис. 5.21), максимальный прогиб по отношению к опорному контуру равен:
|
(5.73) |
|
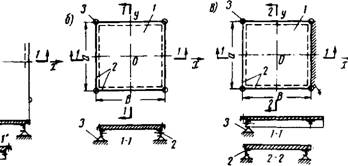
Рис. 5.21. Схемы прямоугольных пластин, опертых по четырем сторонам |
|
А — при свободном опирании на жесткий контур; б — при свободном опирании на упругий контур; В — при свободном опирании на упругий контур по трем сторонам и одной защемленной кромке; 1 — пластина ячейки; 2 — обрамление; 3 — опора |
|
А) |
|
Т1 |
|
I |
|
IL |
|
I 2 " V—-Y—A |
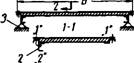
|
Гг х |
Максимальный прогиб квадратной пластины-ячейки на упругом контуре по отношению к опорам по углам определяется по следующим формулам:
А) при свободном опирании на упругий контур по всем кромкам (рис. 5.21,6)
4
In о а
Б) при трех кромках, свободно опертых на упругий контур, и одной защемленной кромке (рис. 5.19, в)
Здесь
Иап
Т[ = 0,22 + 2,87 ;
Ti — коэффициент, определяемый по рис. 5.22 и табл. 29.
Экстремальные значения нормальных напряжений в обшивках в среднем сечении самостоятельной пластины-ячейки, свободно опертой на жесткий контур:
Для квадратной пластины-ячейки в виде самостоятельного элемента на упругом контуре эти значения определяются по следующим формулам:
50 Ад
Рис. 5.22. Графики значений коэффициентов П и п2
А) при свободном опирании на упругий контур по всем кромкам
_ __ 0,049<7 а2
<*в, н = <„ = +----------------------------- Щп ("); (5.75')
Б) при трех кромках, свободно опертых на упругий контур, и одной защемленной кромке (рис. 5.21, б)
|
Таблица 29 Значения коэффициентов пх и п2
|
|
<» - К + "2 "X? ("); (5.75"') |
- _ £пр Си»
Вп? С2"*
Ьп
Т2—коэффициент, определяемый по рис. 5.23; при — >2 принима
Ап
Ется m2 = 1;
П2—коэффицент, определяемый по рис. 5.22 и табл. 29. Наибольшие нормальные на - ^ пряжения в обшивках у опорного контура прямоугольных пластин - ячеек (в точках с координатами
* = 0, у— ±0,5 ап).
<и = см - Рис- 5-21> (5-76)
Те же напряжения для квадратных пластин-ячеек зависят от граничных условий по кромкам.
Для пластин-ячеек на рис. 5.21,6 в точках с координатами
|
(5.77) |
* = 0, у = ±0,5 ап и х= ±0,5 Ь у — = 0:
0х = Оу = Ох =
В, Н В, Н Ц Ц*
Для пластин-ячеек по рис. 5.21, в в точке с координатами х= = ^0,5 Ь; у = 0:
- - 0,085<7п
0в, н = ± Д/ ЪЖи);
В точке с координатами х = —0,5 Ьп; у = 0:
А* = а*:
"в, н ц'
В точке с координатами х=0; у=±0,5 ап:
Ау = оу,
В, н ц
При этом максимальные значения растягивающих напряжений в обшивке не должны превышать а максимальные значения сжимающих напряжений не должны превышать ас.
Наибольшие сдвигающие напряжения в среднем слое пластины:
|
(5.79) |
При'^->2 Ап
_ <?р ап .
|
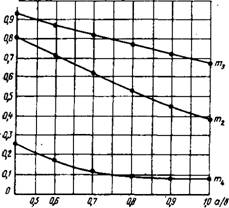
Рис. 5.23. Графики значений коэффициентов Т2, тг и т* |
|
Здесь |
~ 2с '
|
Ьп |
|
<2 |
При 1
|
Т |
|
— 2с |
|
З> |
(5.790
Где т3—коэффициент, определяемый по рис. 5.23.
Значения и, фо(и) и %(и) определяются по рис. 5.24 в зависимости от величины
V =
£пр К
Где /^ — коэффициент распора, характеризующий степень влияния опорного контура на изгиб пластины, определяемый по формуле
Kx>Y -
- ■ • (5.80)
Здесь Z)™pt—изгибная жесткость контура пластины-ячейки в горизонтальной плоскости, определяемая по формуле
Сти трехслойной пластины, включаемой в расчетное сечение контура, определяется по формуле
B™Р= 0,3286п|/ ^ . (5.81)
Расчет пластин-ячеек в системе панели. Расчет пластин-ячеек на усилия, возникающие при их работе в виде самостоятельных элементов (рис. 5.21, а), сводится к определению дополнительных напряжений в частях пластин, примыкающих к элементам обрамления. На этой же стадии производится расчет по прочности и деформациям элементов собственно обрамления.
При этом изгибная жесткость опорного контура может быть под - э формуле
£>ГоРаТт = 1-1+ о, 165 ап D, (5.82)
Где
£)верт = Р J верт обр обр обр •
Ширина приопорной части трехслойной пластины, вовлекаемой в работу при изгибе элементов обрамления в вертикальной плоскости, может быть приближенно определена по формуле
/ 0,0825ап бе2 (5.83)
V I 26 '
Где
Е
Расчет самостоятельных пластин-ячеек. Элементы контура (обрамление совместно с примыкающими к нему участками трехслойных пластин-ячеек) рассчитывается на сжатие с косым изгибом в соответствии с указаниями СНиП II-B.3-62 и СНиП II-B.6-61.
Ширина трехслойной пластины, включаемой в расчетное сечение контура, принимается равной:
А) при расчете на изгиб в плоскости пластины
Ft™Р = 0,328Bn Y^ ;
Б) при расчете на изгиб из плоскости пластины
26
Обр
В) при расчете на сжатие—0,22 bn.
Если обрамления и обшивки выполнены из материалов с разными модулями упругости, это необходимо учитывать при определении геометрических характеристик сечения контура.
Экстремальные напряжения трехслойной пластины у опорного контура (точки 1 с координатами х = 0; у = 0,5ап)
Ох —---------- IEI5-------- 1™------------------- Hi----------- . (5.84)
В 2WfPT /7обр£ + 0,4Шп
Экстремальные напряжения в элементах обрамления пластины - ячейки (точки 2)
О* = Л (-Л*- ^_______ ) . (5.85)
Г2ðРFo6p^+ 0,4466n )
Здесь JF? ePT — моменты сопротивления для соответствующих точек поперечного сечения контура при изгибе в вертикальной плоскости;
|
Считана при — = 1 по формуле |
]F[0p—моменты сопротивления для соответствующих точек поперечного сечения контура пластины при изгибе в горизонтальной плоскости;
Nx = 0,368A* 6ап;
= 0>04656Og 8B2N.
Максимальные сдвигающие напряжения в элементах обрамления пластины-ячейки определяются по формулам, используемым при расчете изгибаемых тонкостенных профилей.
Расчетная величина поперечной силы принимается равной 0,125 <7Р аиЬп .
Максимальный прогиб опорного контура пластины-ячейки в вертикальной плоскости
B^
Е = Ча п • (5.86)
24(Шверт
Z^Ui/ ко н т